Пусть имеется случайная величина 
c непрерывной и дифференцируемой функцией распределения . Вычислим вероятность попадания этой случайной величины на отрезок от 
до 
то есть приращение функции распределения:
.
Рассмотрим среднюю вероятность (т.е. отношение),приходящуюся на единицу длинны на этом участке и будем приближать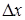 
к нулю. В пределе получаем производную от функции распределения (далее 
).
.
Функция называется плотностью функции распределения непрерывной случайной величины 
или дифференциальным законом распределения случайной величины .
Производная от функции распределения характеризует плотность,с которой распределяются значения случайной величины в данной точке. Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Кривая распределения - график изображающий плотность распределения случайной величины.
Рис. 2
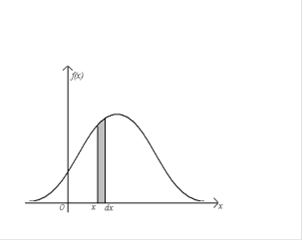
Рис. 3
Элемент вероятности - вероятность попадания случайной величины с плотностью распределения на элементарный участок 
, примыкающий к точке 
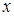. С точки зрения геометрии это площадь элементарного прямоугольника опирающегося на отрезок .
Вероятность попадания случайной величины на отрезок от 
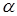до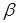 
равна сумме элементов на всем участке, то есть интегралу вида:
.
Выражая функцию распределения через плотность, по определению получаем:
.
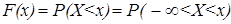Из этого следует, что:
.
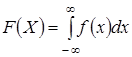Геометрически 
является площадью кривой распределения, лежащей левее точки .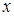
Основные свойства плотности распределения:
1.
2.
Геометрически основные свойства плотности распределения означают, что:
) Вся кривая распределения лежит не ниже оси абсцисс;
) Полная площадь, ограниченная кривой распределения с осью абсцисс равна единице.
Числовые характеристики случайных величин
Математическое ожидание
Рассмотрим дискретную случайную величину , имеющую возможные значения 
с вероятностями 
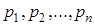. Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым средним взвешенным из значений 
, таким образом, мы вычислим среднее значение случайной величины , которое мы обозначим 
Это среднее взвешенное значение называется математическим ожиданием.
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Для непрерывной величины математическое ожидание выражается интегралом:
Где 
- плотность распределения величины .
Свойства:
1. Математическое ожидание постоянной равно этой постоянной.
.
2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
.
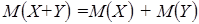Из этого следует, что математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.
.
. Математическое ожидание произведения независимых случайных величин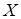 
и 
равно произведению математических ожиданий этих величин.
.
Из этого следует, что постоянный множитель можно вынести за знак математического ожидания:
.
Модой случайной величины называется ее наиболее вероятное значение. Термин наиболее вероятное значение, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна.
Медианой случайной величины 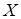называется такое ее значение 
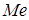, для которого одинаково вероятно, окажется ли случайная величина меньше или больше 
.
.
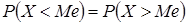Дисперсия
Дисперсией 
называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:
Для непосредственного вычисления дисперсии служат формулы:
.
.
Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания.
Если обратиться к механической интерпретации, то дисперсия представляет собой не что иное, как момент инерции заданного распределения масс относительно математического ожидания.
Дисперсия случайной величины имеет размерность квадрата случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением случайной величины 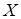. Среднее квадратическое отклонение обозначается 
:
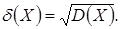
Некоторые свойства дисперсии:
. Дисперсия постоянной величины равна нулю.
. Постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:
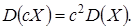
. Дисперсия суммы независимых случайных величин 
и равна сумме их дисперсий:
.
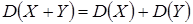Из этого следует если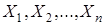 
- случайные величины, каждая из которых независима от суммы остальных, то
4. 
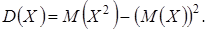
Моменты
Начальным моментом 
- го порядка случайной величины 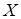называется математическое ожидание - ой степени этой случайной величины.
.
Начальным моментом - го порядка дискретной случайной величины 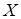является сумма вида:
.
Для непрерывной случайной величины 
начальным моментом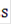 
- го порядка является интеграл:
.
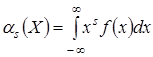Заключение
Таким образом, в работе были рассмотрены основные понятия, связанные с непрерывными случайными величинами. Было показано, что случайные величины могут быть описаны с помощью функции плотности. Также был рассмотрен вопрос о числовых характеристиках случайных величин и их свойствах.
Литература
1. Е.С. Венцтель «Теория вероятностей» - «Наука», 1969.