ГЛАВА 6. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Возрастание функции в точке. Теорема Ферма
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 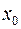 . Говорят, что функция возрастает в точке
. Говорят, что функция возрастает в точке 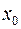 , если существует некоторая окрестность точки
, если существует некоторая окрестность точки 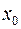
 , в которой функция возрастает, то есть
, в которой функция возрастает, то есть
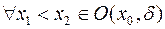

Аналогично определяется убывание функции в точке.
Теорема 1. Если функция  имеет производную в точке
имеет производную в точке 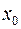 и
и  , то функция возрастает в точке
, то функция возрастает в точке 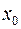 .
.
Доказательство. 
 .
.
Возьмём  , тогда
, тогда
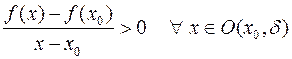 . (1)
. (1)
Неравенство (1) означает, что 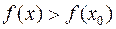 , если
, если  , и
, и  если
если 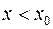 , то есть функция
, то есть функция  возрастает в точке
возрастает в точке 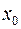 . Теорема доказана.
. Теорема доказана.
Очевидно, если 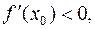 то функция в точке
то функция в точке 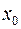 убывает. Доказательство аналогично.
убывает. Доказательство аналогично.
Замечание 1. Условие  – достаточное, для возрастания (убывания) функции в точке
– достаточное, для возрастания (убывания) функции в точке 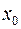 . Но это условие не является необходимым. Например, функция
. Но это условие не является необходимым. Например, функция  возрастает в точке
возрастает в точке  , но
, но 
Определение. Функция  достигает в точке
достигает в точке 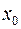 локального максимума, если существует
локального максимума, если существует  такая, что
такая, что

 . (2)
. (2)
 |
Аналогично, если
 , (3)
, (3)
то в точке  функция достигает локального минимума. Локальные максимум и минимум называются локальными экстремумами.
функция достигает локального минимума. Локальные максимум и минимум называются локальными экстремумами.
На рисунке 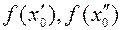 – локальные минимумы,
– локальные минимумы,  – локальный максимум.
– локальный максимум.
Теорема 2 (Ферма). Если функция 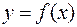 дифференцируема в точке
дифференцируема в точке 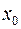 и достигает в этой точке локального экстремума, то
и достигает в этой точке локального экстремума, то 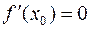 .
.
Доказательство. От противного. Если  , то согласно теореме 1 функция в точке
, то согласно теореме 1 функция в точке  возастает, то есть не достигает локального экстремума. Если р
возастает, то есть не достигает локального экстремума. Если р  , то убывает и также не достигает экстремума. Получили противоречие. Теорема доказана.
, то убывает и также не достигает экстремума. Получили противоречие. Теорема доказана.
Геометрически теорема Ферма означает, что в точке ( , f (
, f ( )) график функции
)) график функции  имеет горизонтальную касательную.
имеет горизонтальную касательную.
Теоремы о среднем
Теорема 1 (Ролль). Если функция 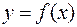 непрерывна на отрезке
непрерывна на отрезке 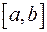 , дифференцируема на интервале
, дифференцируема на интервале  а на концах отрезка принимает равные значения
а на концах отрезка принимает равные значения  , то существует, по крайней мере, одна точка
, то существует, по крайней мере, одна точка  , в которой
, в которой 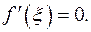
Доказательство. Так как функция  непрерывна на отрезке
непрерывна на отрезке 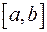 , то, согласно второй теореме Вейерштрасса (см. §10 гл. 4), она достигает на нём своего наименьшего
, то, согласно второй теореме Вейерштрасса (см. §10 гл. 4), она достигает на нём своего наименьшего  и наибольшего
и наибольшего 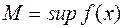 значений.
значений.
Возможны два случая:
а)  – const, следовательно,
– const, следовательно, 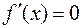 Теорема доказана.
Теорема доказана.
б) 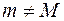 . Так как
. Так как 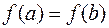 , то, по крайней мере, одно из чисел
, то, по крайней мере, одно из чисел  или
или  отлично от
отлично от  .
.
Допустим  . Тогда
. Тогда  , где
, где  . Это означает, что функция
. Это означает, что функция 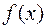 достигает в точке
достигает в точке 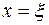 локального максимума. По теореме Ферма
локального максимума. По теореме Ферма  . Что и требовалось доказать.
. Что и требовалось доказать.
Геометрически теорема Ролля означает, что между двумя точками, в которых значения функции равны, всегда найдётся точка, касательная в которой параллельна оси  .
.
Следствие. Если функция непрерывна на 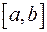 , дифференцируема на
, дифференцируема на 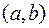 , но
, но  , то
, то  . Доказательство от противного.
. Доказательство от противного.
Теорема 2 (Коши). Если функции 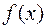 и
и  непрерывны на
непрерывны на 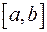 , дифференцируемы на
, дифференцируемы на 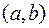 , причем
, причем 
 , то существует точка
, то существует точка  такая, что
такая, что
 (1)
(1)
Доказательство. Составим вспомогательную функцию  , где
, где  – некоторый коэффициент. Подберём его так, чтобы функция
– некоторый коэффициент. Подберём его так, чтобы функция  удовлетворяла условиям теоремы Ролля, то есть потребуем равенства на концах отрезка
удовлетворяла условиям теоремы Ролля, то есть потребуем равенства на концах отрезка 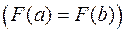 , так как все другие требования теоремы Ролля выполняются).
, так как все другие требования теоремы Ролля выполняются).
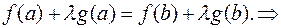
 . (2)
. (2)
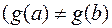 согласно следствию теоремы Ролля).
согласно следствию теоремы Ролля).
Итак, если коэффициент  определяется формулой (2), то функция
определяется формулой (2), то функция  удовлетворяет теореме Ролля, то есть
удовлетворяет теореме Ролля, то есть

Или
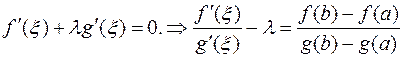 .
.
Теорема доказана.
Теорема 3 (Лагранж). Если функция  непрерывна на отрезке
непрерывна на отрезке 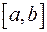 и дифференцируема на интервале
и дифференцируема на интервале 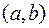 , то существует точка
, то существует точка  такая, что
такая, что
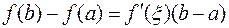 . (3)
. (3)

Доказательство. Положив в теореме Коши 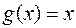 , получим
, получим
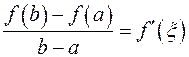 или
или 
Теорема доказана.
Из рис. видно, что  где
где  – угол наклона секущей
– угол наклона секущей 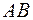 , а из (3) видно, что
, а из (3) видно, что 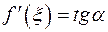 , то есть теорема Лагранжа утверждает, что между точками
, то есть теорема Лагранжа утверждает, что между точками  и
и  кривой существует точка
кривой существует точка  такая, что касательная в этой точке параллельна секущей.
такая, что касательная в этой точке параллельна секущей.
Замечание. Пусть  удовлетворяет теореме Лагранжа и пусть
удовлетворяет теореме Лагранжа и пусть  Тогда согласно (3)
Тогда согласно (3)

или 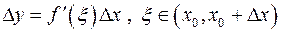 . (
. ( )
)
Или  где
где  Равенства (
Равенства ( ) и (3) называют формулой конечных приращений. Формула (
) и (3) называют формулой конечных приращений. Формула ( ) – это точное равенство для любых конечных
) – это точное равенство для любых конечных  (в отличие от приближённого
(в отличие от приближённого  ).
).
Во всех трёх теоремах речь идёт о существовании некоторой средней точки  , поэтому эти теоремы и называют теоремами о среднем.
, поэтому эти теоремы и называют теоремами о среднем.
Некоторые следствия из теоремы Лагранжа. Теорема Дарбу
Теорема 1. Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Тогда:
. Тогда:
а) если  , то функция монотонно убывает;
, то функция монотонно убывает;
б) если 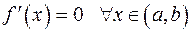 , то
, то  ;
;
в) если 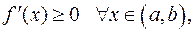 то функция монотонно возрастает.
то функция монотонно возрастает.
Доказательство. Пусть 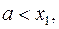
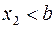 ,
,  – произвольные точки. Тогда на отрезке
– произвольные точки. Тогда на отрезке  функция
функция  удовлетворяет теореме Лагранжа.
удовлетворяет теореме Лагранжа.
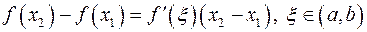 . (*)
. (*)
Если  то
то  и из (*) следует
и из (*) следует  , то есть функция
, то есть функция  убывает монотонно на
убывает монотонно на  . Утверждение а) теоремы 1 доказано.
. Утверждение а) теоремы 1 доказано.
Утверждения б) и в) доказываются аналогично.
Теорема 2 (Дарбу). Пусть функция  дифференцируемая на
дифференцируемая на  и пусть
и пусть  . Тогда найдётся точка
. Тогда найдётся точка  такая, что
такая, что 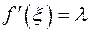 , то есть функция
, то есть функция 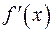 подобно непрерывной функции принимает все свои промежуточные значения между
подобно непрерывной функции принимает все свои промежуточные значения между  и
и 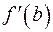 .
.
Доказательство. Пусть  (если
(если  – доказательство аналогично). Положим
– доказательство аналогично). Положим 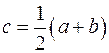 и введём две функции
и введём две функции
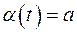 и
и  , если
, если  . (1)
. (1)
 и
и  , если
, если  . (2)
. (2)

Тогда
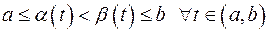 (3)
(3)
(см. рис.). Рассмотрим сложную функцию
 . (4)
. (4)
Очевидно,  непрерывна на
непрерывна на  как суперпозиция, разность и отношение непрерывных функций. Найдём предел
как суперпозиция, разность и отношение непрерывных функций. Найдём предел

 .
.
(Производная  существует по условию теоремы).
существует по условию теоремы).
Аналогично найдём

Доопределим функцию  , положив
, положив
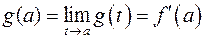
и 
Тогда функция  будет непрерывной на отрезке
будет непрерывной на отрезке 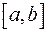 и по теореме Коши (см. §11) принимает все свои промежуточные значения, то есть если
и по теореме Коши (см. §11) принимает все свои промежуточные значения, то есть если
 ,
,
или  ,
,
то найдётся точка  такая, что
такая, что
 . (5)
. (5)
Зафиксируем 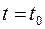 и из (4) найдём:
и из (4) найдём:
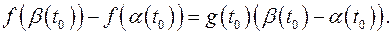 (6)
(6)
Но на отрезке 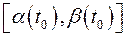 функция
функция  удовлетворяет теореме Лагранжа (см. теорему 3 §2)
удовлетворяет теореме Лагранжа (см. теорему 3 §2)
 Сравнивая (6) и(7), получим
Сравнивая (6) и(7), получим
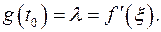
Что и требовалось доказать.
Следствие. Если функция  дифференцируема на отрезке
дифференцируема на отрезке  , то её производная
, то её производная  не имеет точек разрыва первого рода.
не имеет точек разрыва первого рода.

Доказательство. От противного. Пусть существует функция  дифференцируемая на
дифференцируемая на  , а её производная
, а её производная  строго возрастает на
строго возрастает на  и имеет в точке
и имеет в точке 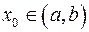 разрыв первого рода (см. рис.). Пусть
разрыв первого рода (см. рис.). Пусть
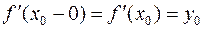
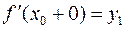
и пусть
 . (8)
. (8)
Согласно теореме 2 производная  примет значение
примет значение  , причём
, причём  , так как
, так как  строго возрастает. В силу строгой монотонности
строго возрастает. В силу строгой монотонности
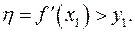
Получили противоречие (см. (8)). Это противоречие и доказывает следствие.