Лекция 6
Тема «Понятие системы линейных уравнений.
Условия разрешимости системы»
Цель: формирование понятия системы линейных уравнений (СЛУ), ее видов и представлении в матричной форме4 ознакомление с условиями разрешимости системы.
План лекции:
1. Понятие СЛУ, виды систем.
2. Представление СЛУ в матричной форме.
3. Ранг матрицы. Условия разрешимости системы линейных уравнений.
Основные понятия: система линейных уравнений; совместные, несовместные, определенные, однородные и неоднородные системы.
Понятие системы линейных уравнений. Виды СЛУ
ОПР. Система уравнений следующего вида
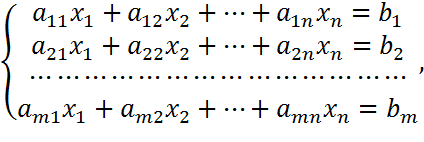
где 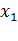 ,
, 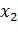 ,…,
,…, 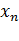 - неизвестные, подлежащие определению,
- неизвестные, подлежащие определению,
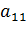 ,…,
,…, 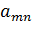 - коэффициенты системы,
- коэффициенты системы, 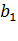 ,
, 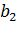 ,…,
,…, 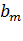 - свободные члены, называется системой линейных уравнений (СЛУ).
- свободные члены, называется системой линейных уравнений (СЛУ).
ПРИМЕР. 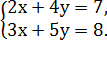 – система линейных уравнений
– система линейных уравнений
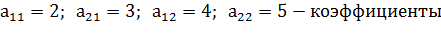
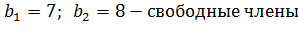
х и у – переменные
ОПР. Решить систему линейных уравнений – значит указать все решения системы, т.е. такие наборы значений переменных, которые обращают уравнения в тождества.
ПРИМЕР. х = -1,5 и у = 2,5 – решение системы, т.к.
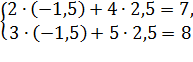 ⇒
⇒ 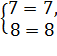 тождества
тождества
ОПР. Система линейных уравнений называется:
А) совместной, если она имеет хотя бы одно решения, и несовместной – если СЛУ решений не имеет;
Б) определенной, если система имеет единственное решение;
В) однородной, если все свободные члены 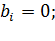
Г) неоднородной, если есть хотя бы один свободный член не равен нулю.
ПРИМЕР.
Система линейных уравнений 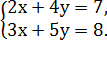 – совместная, определенная и неоднородная, т.к. х = -1,5 и у = 2,5 – единственное решение и
– совместная, определенная и неоднородная, т.к. х = -1,5 и у = 2,5 – единственное решение и 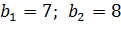 – свободные члены, не равные нулю.
– свободные члены, не равные нулю.
ОПР. Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение.
ВАЖНО! Эквивалентные системы получаются, в частности при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками системы.
ПРИМЕР.
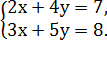 и
и 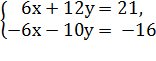 – эквивалентные системы
– эквивалентные системы
Вторая СЛУ получена из первой путем элементарного преобразования: первое уравнение до множено на 3, а второе до множено на число (-2).
Представление СЛУ в матричной форме
Систему линейных уравнений 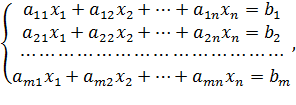 удобно записывать в компактной матричной форме
удобно записывать в компактной матричной форме 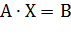 ,
,
где А – матрица коэффициентов системы, называемая основной матрицей
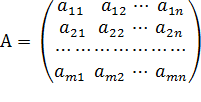 ,
, 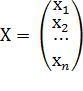 – вектор – столбец из неизвестных
– вектор – столбец из неизвестных 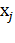 ,
,
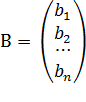 - вектор – столбец из свободных членов
- вектор – столбец из свободных членов 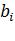 .
.
Произведение матриц А∙Х определено, т.к. в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
ОПР. Расширенной матрицей системы называется матрица 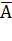 системы, дополненная столбцом свободных членов
системы, дополненная столбцом свободных членов 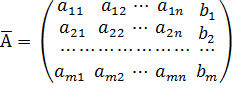 .
.
Всякое решение СЛУ можно записать в виде матрицы – столбца 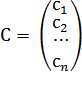 .
.
ПРИМЕР.
СЛУ 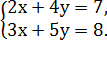 Основная матрица
Основная матрица 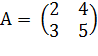
Расширенная матрица 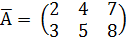
Ранг матрицы. Условия разрешимости системы линейных уравнений
Пусть система m линейных уравнений с n неизвестными в общем виде имеет следующий вид:
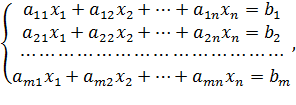
Исчерпывающий ответ на вопрос о совместности этой СЛУ (т.е. о наличии хотя бы одного решения системы) дает теорема Кронекера – Капелли.
Обозначение: r(А) – «ранг матрицы А».
Ранг нулевой матрицы равен 0.
Алгоритм нахождения ранга матрицы методом перебора миноров:
Пусть дана матрица А порядка m x n.
1. при наличии хотя бы одного элемента, отличного от 0, то ранг матрицы как минимум равен 1 (т.к. есть минор 1-ого порядка, который не равен 0);
2. перебираем миноры 2-ого порядка; если все миноры 2-ого порядка равны 0, то ранг равен 1.; при существовании хотя бы одного не равного нулю минора 2-ого порядка, необходимо перейти к перебору миноров 3-его порядка, а ранг матрицы, в таком случае, будет равен минимум 2;
3. аналогичным образом поступим с рангом 3-его порядка: если все миноры матрицы равняются 0, то ранг будет равен 2; при наличии хотя бы одного ненулевого минора 3-его порядка, то ранг матрицы равен минимум 3.
И так далее, по аналогии.
ПРИМЕР. Найти ранг матрицы 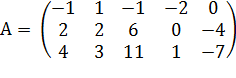 .
.
1. Поскольку матрица ненулевая, то r(A) минимум равен 1.
2. Минор 2-ого порядка 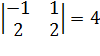 – не равен 0. Тогда r(А) минимум 2.
– не равен 0. Тогда r(А) минимум 2.
3. Минор 3 – его порядка: 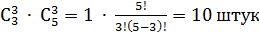 .
.
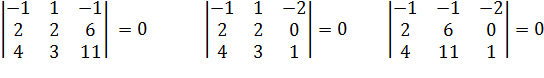
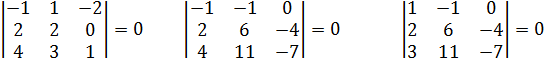
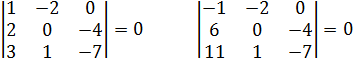
Все миноры 3 – его порядка равны нулю.
Ответ: r(A) = 2.
ТЕОРЕМА 1. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
А – основная матрица 
СЛУ имеет хотя бы одно решение 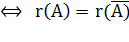 .
.
ТЕОРЕМА 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
ТЕОРЕМА 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
ПРИМЕР. Исследовать на совместность систему 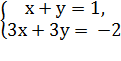 .
.
Исследовать на совместность систему – это значит выяснить, имеет ли СЛУ решения и сколько.
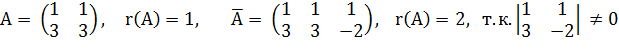
Таким образом, r(A) ≠ r(A). Следовательно, система несовместна.
Ответ: СЛУ несовместна.
ПРИМЕР. Исследовать на совместность систему
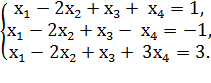
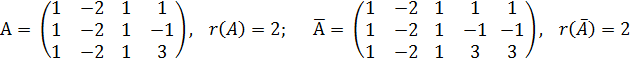
Получаем, что r(A)  r(A), тогда СЛУ имеет решение и СЛУ совместна.
r(A), тогда СЛУ имеет решение и СЛУ совместна.
Ответ: СЛУ совместна.
Задача 1. Найдите ранг матриц:
1) 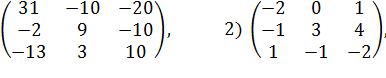
3) 
Критерии оценивания:
«5» - 3 балла;
«4» - 2 балла;
«3» - 1 балл;
«2» - 0 баллов.