Нормальный эллиптический интеграл 1-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 1-го рода {\displaystyle F}F определяется как
или, в форме Якоби,
Обозначения эллиптических интегралов не являются универсально общепринятыми. Следует различать такие разделители между переменной и параметром, как «\», «|» и «,». Там, где в качестве разделителя используется вертикальная черта, за ней ставится параметр интеграла, тогда как за обратной косой чертой ставится модулярный угол. В частности, верно соотношение
Нормальный эллиптический интеграл 2-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 2-го рода E определяется как
или, используя подстановку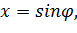 
{\displaystyle x=\sin \varphi,}
Нормальный эллиптический интеграл 3-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 3-го рода П{\displaystyle \Pi } определяется как
Или
Число {\displaystyle c}c называется характеристикой и может принимать любое значение, независимо от остальных аргументов. Свойства эллиптического интеграла 3-го рода существенно зависят от величины характеристики. Заметим, что значение интеграла
{\displaystyle \Pi (-1;\;\pi /2\mid m)} стремится к бесконечности для любых {\displaystyle m} m.
Полный нормальный эллиптический интеграл Лежандра 1-го рода
В случае, если амплитуда {\displaystyle \varphi } нормального эллиптического интеграла Лежандра 1-го рода равна {\displaystyle \pi /2}, он называется полным нормальным эллиптическим интегралом Лежандра 1-го рода:
{\displaystyle K(k)=\int \limits _{0}^{\pi /2}\!{\frac {d\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}}=F(\pi /2,\;k)}
или
{\displaystyle K(k)=\int \limits _{0}^{\pi /2}\!{\frac {d\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}}=F(\pi /2,\;k)}
{\displaystyle K(k)=\int \limits _{0}^{1}\!{\frac {dx}{\sqrt {(1-x^{2})(1-k^{2}x^{2})}}}.}
Полный эллиптический интеграл 1-го рода можно представить в виде степенного ряда:
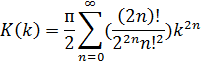
что эквивалентно выражению
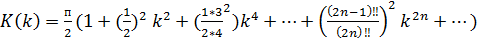{\displaystyle K(k)=\int \limits _{0}^{\pi /2}\!{\frac {d\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}}=F(\pi /2,\;k)}
{\displaystyle K(k)={\frac {\pi }{2}}\left(1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\ldots +\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}k^{2n}+\ldots \right),}
где {\displaystyle n!!}n!! обозначает двойной факториал.
Полный эллиптический интеграл 1-го рода можно записать через гипергеометрическую функцию следующим образом:
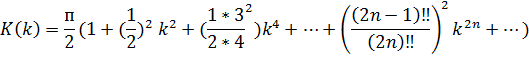
Полный нормальный эллиптический интеграл Лежандра 2-го рода
В случае, если амплитуда {\displaystyle \varphi } нормального эллиптического интеграла Лежандра 2-го рода равна {\displaystyle \pi /2}, он называется полным нормальным эллиптическим интегралом Лежандра 2-го рода:
{\displaystyle E(k)=\int \limits _{0}^{\pi /2}\!{\sqrt {1-k^{2}\sin ^{2}\varphi }}\,d\varphi =E(\pi /2,\;k)}
Или
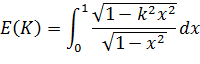
{\displaystyle E(k)=\int \limits _{0}^{1}\,{\frac {\sqrt {1-k^{2}x^{2}}}{\sqrt {1-x^{2}}}}\,dx.}
Полный эллиптический интеграл 2-го рода можно представить в виде степенного ряда:
{\displaystyle E(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}n!^{2}}}\right)^{2}{\frac {k^{2n}}{1-2n}},}
что эквивалентно выражению
{\displaystyle K(k)=\int \limits _{0}^{\pi /2}\!{\frac {d\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}}=F(\pi /2,\;k)}
{\displaystyle E(k)={\frac {\pi }{2}}\left(1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\ldots -\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {k^{2n}}{2n-1}}-\ldots \right).}
Полный эллиптический интеграл 2-го рода можно записать через гипергеометрическую функцию следующим образом:
{\displaystyle E(k)={\frac {\pi }{2}}\,_{2}F_{1}\left({\frac {1}{2}},\;-{\frac {1}{2}};\;1;\;k^{2}\right).}