Понятие ряда Фурье
Тригонометрическим рядом Фурье называется ряд вида:
или, короче,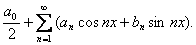 
где числа 
- коэффициенты Фурье.
Коэффициенты Фурье вычисляются по следующим формулам:
,
,
.
Таким образом, в отличие от степенного ряда, в ряде Фурье вместо простейших функций 
взяты тригонометрические функции
Все вышеперечисленные функции являются периодическими функциями с периодом 
. Каждый член тригонометрического ряда Фурье является периодической функцией с периодом . Поэтому и любая частичная сумма ряда Фурье -периодична. Отсюда следует, что если ряд Фурье сходится на отрезке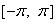 
, то он сходится на всей числовой прямой и его сумма, будучи пределом последовательности периодических частичных сумм, является периодической функцией с периодом .
Вышеупомянутое свойство видно на графике внизу: здесь график суммы ряда для функции f (x) = x. Вне отрезка 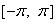сумма ряда является периодическим продолжением данной функции, то есть график функции бесконечно повторяется справа и слева.
Сходимость ряда Фурье и сумма ряда
Пусть функция 
, определённая на всей числовой прямой и периодическая с периодом , является периодическим продолжением функции f (x), если на отрезке 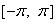F (x) = f (x)
Если на отрезке 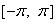ряд Фурье сходится к функции f (x), то он сходится на всей числовой прямой к её периодическому продолжению.
Ответ на вопрос о том, при каких условиях ряд Фурье функции f (x) сходится к этой функции, даёт следующая теорема.
Теорема. Пусть функция f (x) и её производная f ' (x) - непрерывные на отрезке 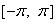или же имеют на нём конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции f (x) сходится на всей числовой прямой, причём в каждой точке 
, в которой f (x) непрерывна, сумма ряда равна f (x), а в каждой точке 
разрыва функции сумма ряда равна
,
где 
и 
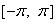. На концах отрезка сумма ряда равна
.
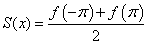В любой точке сумма ряда Фурье равна F (x), если x - точка непрерывности F (x), и равна
,
если x - точка разрыва F (x), где F (x) - периодическое продолжение f (x).
Ряды Фурье для чётных и нечётных функций
Пусть функция f (x) определена на отрезке 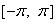и является чётной, т. е. f (- x) = f (x). Тогда её коэффициенты 
равны нулю. А для коэффициентов 
верны следующие формулы:
,
.
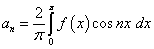Пусть теперь функция f (x), определённая на отрезке 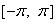, нечётная, т.е. f (x) = - f (- x). Тогда коэффициенты Фурье равны нулю, а коэффициенты определяется формулой
.
Таким образом, если функция f (x) чётная, то ряд Фурье содержит только косинусы, а если нечётная, то только синусы.
Пример 1. Разложить в ряд Фурье функцию 
.
Решение. Это нечётная функция, поэтому её коэффициенты Фурье 
, а чтобы найти , нужно вычислить определённый интеграл:
Таким образом, получаем ряд Фурье данной функции:
.
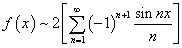Это равенство справедливо для любого . В точках 
сумма ряда Фурье по приведённой во втором параграфе теореме не совпадает со значениями функции , а равна 
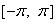. Вне отрезка сумма ряда является периодическим продолжением функции , её график приводился выше в качестве иллюстрации суммы ряда.
Пример 2. Разложить в ряд Фурье функцию 
.
Решение. Это чётная функция, поэтому её коэффициенты Фурье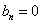 
, а чтобы найти , нужно вычислить определённые интегралы:
Таким образом, получаем ряд Фурье данной функции:
.
Это равенство справедливо для любого , так как в точках сумма ряда Фурье в данном случае совпадает со значениями функции , поскольку 
.
Ряды Фурье с периодом 2 l
Пусть функция f (x) определена на отрезке [- l, l ] (l - произвольное положительное число). Тогда формула ряда Фурье этой функции принимает вид
,
где
,
,
.
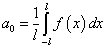Пример 3. Разложить в ряд Фурье с периодом 2 l функцию f (x), которая на отрезке [- l, l ] задаётся формулой 
.
Решение. Это чётная функция, поэтому её коэффициент Фурье 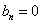, а чтобы найти , нужно вычислить определённые интегралы:
Таким образом, получаем ряд Фурье данной функции:
.
Это равенство справедливо для любого , а это значит, что ряд сходится на всей числовой прямой.