О.А. Емельянов, Н.В. Коровкин, Е.Ю. Кочеткова,
Т.Г. Миневич, А.Н. Модулина, Л.И. Сахно
РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
Учебное пособие
Санкт-Петербург
ПРЕДИСЛОВИЕ
Задача настоящего пособия — помочь студентам в работе над курсовым проектом, выполняемым при изучении дисциплины «Теоретические основы электротехники» (раздел «Теория электромагнитного поля»).
Тематика курсового проекта связана с расчетом электростатического поля. В предлагаемом пособии рассматривается расчет электростатического поля конденсаторов различного типа. Задание по курсовому проекту содержит несколько разделов, носящих вариативный характер, выполнение которых требует от студентов творческого подхода. Разделы, связанные с наличием в межэлектродном пространстве объемного заряда, имеют прикладное значение.
Для успешной работы над курсовым проектом необходимо предварительное изучение соответствующего теоретического материала по учебнику [1]. Теоретическая часть пособия дополняется примерами с подробными решениями, которые охватывают основные разделы задания и могут служить образцом при выполнении проекта. Предлагаемые варианты заданий достаточно разнообразны, что позволит преподавателю – руководителю проекта сформировать для каждого студента индивидуальные задания необходимого объема и сложности.
ЗАДАНИЕ
РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
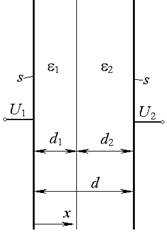
1. Вывести выражения и рассчитать распределения потенциала и напряженности электростатического поля в пространстве между электродами плоского, цилиндрического или сферического конденсатора с двухслойным диэлектриком (рис. 1, а, 1, б и 1, в соответственно). Построить графики полученных зависимостей U (x) и E (x) для плоского конденсатора, U (r) и E (r) – для цилиндрического и сферического в случаях, когда:
а)
| б)
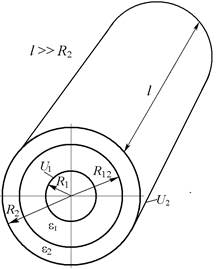
| в)
|
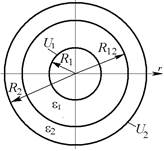
| Рис. 1 |
1.1 между электродами помещен двухслойный диэлектрик с абсолютными диэлектрическими проницаемостями слоев e1 и e2; конденсатор подключен к источнику ЭДС с напряжением U 1= U 0, второй электрод заземлен — U 2=0;
1.2. двухслойный диэлектрик заменен однородным диэлектриком с абсолютной проницаемостью e1=e2=e3; замена произведена при подключенном к электродам конденсатора источнике ЭДС;
1.3. двухслойный диэлектрик заменен однородным диэлектриком с абсолютной проницаемостью e1=e2=e3; замена произведена после отключения конденсатора от источника ЭДС.
Во всех рассмотренных случаях определить поверхностную плотность зарядов s каждого из электродов. Для плоского и сферического конденсаторов найти заряды q каждого из электродов, а также ёмкость C системы. Для цилиндрического конденсатора заряд электродов и ёмкость определяются на единицу его длины: t= q /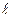 
, 
.
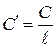2. Получить и построить зависимости максимальной напряженности поля E max, зарядов q 1, q 2 каждого из электродов и поверхностной плотности зарядов s1, s2 на них, а также емкости системы от одного из параметров конденсатора: R 1, R 12, R 2, e1 или e2. При этом все остальные параметры остаются неизменными.
3. Определить, при каком значении радиуса граничной поверхности слоев диэлектрика приложенное к конденсатору напряжение делится поровну между слоями диэлектрика: 
.
4. Определить значение параметра задачи, указанного преподавателем, обеспечивающее равенство максимальных величин напряженности поля в каждом из слоев диэлектрика.
5. Получить выражения для потенциала и напряженности поля в пространстве между электродами конденсатора в случае, когда в одну из областей внесен объемный заряд с плотностью r, распределенный по заданному закону в зависимости от координаты, перпендикулярной поверхности электродов (x – для плоского конденсатора, r – для цилиндрического и сферического). При этом один из электродов заземлен, другой присоединен к источнику напряжения U 0.Построить графики зависимости потенциала и напряженности поля от координаты.
6. Решить задачу для случая, когда полярность электродов U 1, U 2 изменена на обратную. Сравнить максимальные значения напряженности в обоих случаях. Определить пробивное значение напряжения между электродами конденсатора при заданной пробивной напряженности электрического поля в диэлектрике.
Значения параметров конденсаторов приведены в таблицах 1, 2.
Таблица 1. Параметры цилиндрического (1–8) и сферического (9–16)
конденсаторов
| Вариант | 1(9) | 2 (10) | 3(11) | 4 (12) | 5 (13) | 6(14) | 7(15) | 8(16) |
| R 1, см | ||||||||
| R 12, см | 1,5 | 2,5 | 4,5 | 4,5 | ||||
| R 2, см | 3,5 | 5,5 | ||||||
| ε1 r | ||||||||
| ε2 r | ||||||||
| e3 r | ||||||||
| U 0, В | ||||||||
| r0, Кл/м3 | 5 10-4 | 2 10-4 | 8 10-4 | 3 10-3 | 2 10-4 | 2 10-4 | 8 10-4 | 5 10-3 |
| α, Кл/м4 | – | 2 10-4 | – | – | – | 2 10-4 | – | – |
| b, м-1 | – | – | – | – | ||||
| Варьируемый параметр (для п.2) | R 1 | R 12 | R 2 | e1 | e2 | R 1 | R 12 | R 2 |
| Варьируемый параметр (для п.4) | e1 | R 1 | e1 | R 12 | R 1 | e1 | R 1 | e2 |
| Пробивная напряженность, 107 В/м |
В вар. 1, 9: r2=r0=const;
В вар. 2, 10: r2=– α(– r + R 12), R 12< r < R 2;
В вар. 3, 4, 11, 12: r2=r0 e b( r – R 12), R 12< r < R 2;
В вар. 5, 13: r1=r0=const;
В вар. 6, 14: r1= α(– r + R 12), R 1< r < R 12;
В вар. 7, 8, 15, 16: r1=r0 e b( r – R 1), R 1< r < R 12.
Таблица 2. Параметры плоского конденсатора
| Вариант | 1 (9) | 2 (10) | 3 (11) | 4 (12) | 5 (13) | 6 (14) | 7 (15) | 8 (16) |
| d 1 см | 1,5 | 2,5 | 3,5 | 3,5 | ||||
| d 2 см | 1,5 | 2,5 | 4,5 | 4,5 | ||||
| ε1 r | ||||||||
| ε2 r | ||||||||
| e3 r | ||||||||
| U 0, В | ||||||||
| r0, Кл/м3 | 5 10-4 | 2 10-4 | 8 10-4 | 3 10-3 | 2 10-4 | 2 10-4 | 8 10-4 | 5 10-3 |
| α, Кл/м4 | – | 2 10-4 | – | – | – | 2 10-4 | – | – |
| b, м-1 | – | – | – | – | ||||
| Варьируемый параметр (для п.2) | R 1 | R 12 | R 2 | e1 | e2 | R 1 | R 12 | R 2 |
| Варьируемый параметр (для п.4) | e1 | R 1 | e1 | R 12 | R 1 | e1 | R 1 | e2 |
| Пробивная напряженность, 107 В/м |
В вар. 1, 9: r2=r0=const;
В вар. 2, 10: r2=–α(– x + d 1), d 1< x < d 1+ d 2;
В вар. 3, 4, 11, 12: r2=r0 e b( x – d 1), d 1< x < d 1+ d 2;
В вар. 5, 13: r1=r0=const;
В вар. 6, 14: r1= α(– x + d 1), 0< x < d 1;
В вар. 7, 8, 15, 16: r1=r0 e –b x, 0< x < d 1.
Здесь ε1 r, ε2 r, ε3 r – относительные диэлектрические проницаемости, ρ1, ρ2 – объемные плотности заряда в первом и втором слоях диэлектрика соответственно, α, β, ρ0 – параметры, характеризующие распределение объемного заряда в слое диэлектрика.
Примечание. По указанию преподавателя могут задаваться иные значения U 1, U 2, e3, а также других параметров.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Задачей расчета электрического поля является определение напряженности поля во всех его точках по заданным зарядам или потенциалам тел [1]. Для электростатического поля задача полностью решается отысканием потенциала как функции координат. Связь между напряженностью электрического поля и распределением потенциала в пространстве устанавливается соотношением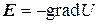 
. Если задан закон распределения свободных зарядов в пространстве как функция координат ρ(x, y, z), то задача отыскания распределения потенциала U (x, y, z) сводится к решению уравнения Пуассона
.
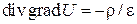При отсутствии объемного заряда r=0 поле описывается уравнением Лапласа
.
Записанные в выбранной системе координат, учитывающей симметрию системы, оба эти уравнения являются дифференциальными уравнениями в частных производных. В тех случаях, когда потенциал является функцией только одной координаты (в задании рассматриваются именно такие случаи), уравнение Пуассона (или Лапласа) переходит из уравнения в частных производных в обыкновенное дифференциальное уравнение второго порядка.
При интегрировании уравнений Пуассона или Лапласа в решении появляются постоянные интегрирования. Их определяют, исходя из граничных условий — условий, которым подчиняется потенциал на границах раздела сред с разными электрическими свойствами.
Условие на границе раздела проводящего тела и диэлектрика.
На границе раздела проводящее тело-диэлектрик при отсутствии электрического тока в проводящем теле выполняются два граничных условия.
1. Отсутствует касательная к поверхности (тангенциальная) составляющая напряженности поля:
.
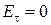Следовательно, на поверхности проводника (как и во всем объеме проводника) потенциал постоянен: U = const.
2. Нормальная составляющая вектора электрического смещения в диэлектрике на поверхности раздела «проводник-диэлектрик» численно равна поверхностной плотности заряда σ на поверхности проводящего тела:
.
Это условие может быть записано через производную потенциала в виде
.
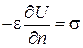Условие на границе раздела двух диэлектриков.
На границе раздела двух диэлектриков с различными диэлектрическими проницаемостями ε1 и ε2 (индекс 1 относится к первому диэлектрику, индекс 2 – ко второму) выполняются два следующих условия:
и, при отсутствии на границе поверхностно распределенного заряда s=0,
..
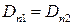Применительно к потенциалу первое условие записывается как
,
второе условие – как
.
ПРИМЕРЫ
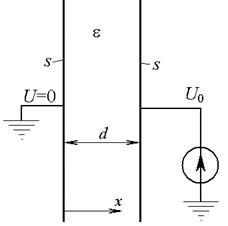
ПРИМЕР 1. В плоском конденсаторе (рис. 2, а) с однослойным диэлектриком с абсолютной диэлектрической проницаемостью 
, потенциал правого электрода равен 
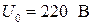, левый электрод заземлен. Расстояние d =1 cм между электродами конденсатора существенно меньше размеров, определяющих их площадь 
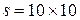=102 см2. Рассчитать распределение потенциала и напряженности электрического поля между электродами конденсатора. Определить поверхностную плотность заряда электродов и их полный заряд для случаев, когда
1.1. между электродами конденсатора отсутствует объемный заряд;
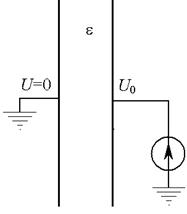
1.2. в пространство между электродами внесен объемный заряд с постоянной плотностью r=2,5·10–4 Кл/м3 = const, при этом правый электрод конденсатора подключен к источнику ЭДС, левый заземлен (рис. 2, б).
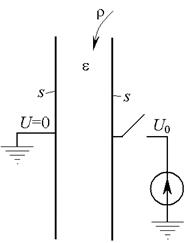
1.3. заряженный конденсатор (рис. 3, а) отключается от источника, при этом левый электрод остается заземленным (рис. 3, б), после чего в пространство между его электродами вносится объемный заряд с постоянной плотностью r=2,5·10–4 Кл/м3=const (рис. 3, в).
1.4. По результатам п.1.1 (в отсутствие объемного заряда между электродами) определить емкость конденсатора.
а)
| б)
|
| Рис. 2 |
а)
| б)
| в)
|
| Рис. 3 |
РЕШЕНИЕ
1.1. Направим ось х перпендикулярно поверхностям пластин, как показано на рис. 2, а. Согласно условию задачи, размеры электродов конденсатора значительно больше расстояния между ними. В этом случае можно не учитывать эффекты искажения поля вблизи краев электродов. Это позволяет считать, что в пространстве между ними вектор напряженности поля направлен вдоль оси х, а его величина зависит только от х: E = f (x).
Уравнение Лапласа в декартовой системе координат имеет вид:
.
В рассматриваемой задаче проекции Ey =0 и Ez =0. Поэтому уравнение Лапласа переходит в обыкновенное дифференциальное уравнение второго порядка:
.
Выполнив двукратное интегрирование по х, получим решение в виде:
;
.
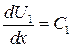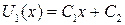Константы С 1 и С 2 определяются из граничных условий:
1. x =0, U =0, следовательно, С 2=0;
2. x=d, U=U 0, откуда следует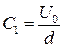 
.
Таким образом, потенциал и напряженность поля определяются выражениями
; 
.
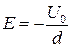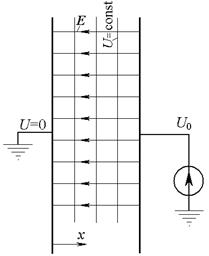
Из полученных выражений видно, что в пространстве между электродами конденсатора потенциал изменяется по линейному закону (рис. 4, а), а напряженность поля имеет постоянное значение.
а)
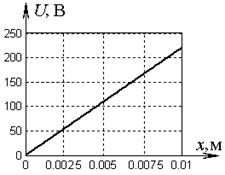
| б)
|
| Рис. 4 |
На рис. 4, б приведена картина поля в пространстве между электродами конденсатора. Вектор напряженности направлен против координаты x в сторону от электрода с большим потенциалом в сторону электрода с меньшим потенциалом.
В пространстве между электродами с равными по величине зарядами противоположных знаков векторы напряженности поля направлены в одну сторону, и суммарная напряженность равна удвоенной, создаваемой каждым из электродов в отдельности. Напротив, в пространстве вне конденсатора эти векторы направлены в противоположные стороны и компенсируют друг друга. Действительно, поток вектора электрического смещения сквозь замкнутую поверхность, охватывающую весь конденсатор, равен нулю, т.к. суммарный заряд электродов равен нулю. Поэтому поле вне конденсатора отсутствует.
Определим поверхностные плотности зарядов на электродах s1 и s2. Напряженность поля и вектор электрического смещения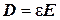 
, имеющие только одну составляющую 
и 
, направлены по оси x: 
, 
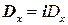(рис. 5), i – соответствующий орт, при этом они имеют знак «минус», что указывает на отрицательное направление векторов E и D по отношению к оси x (рис. 4).
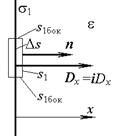
Для расчета поверхностной плотности заряда охватим некоторую часть D s поверхности левого электрода замкнутой поверхностью s 1 (рис. 5, а) в виде прямоугольного параллелепипеда, вертикальные части которого параллельны электроду конденсатора. Выражение для потока вектора смещения через поверхность s 1 в соответствии с постулатом Максвелла принимает вид:
.
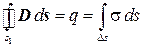Вектор D не пересекает горизонтальные участки s 1бок поверхности s 1, следовательно, поток вектора D через эти участки равен нулю 
.
а)
| б)
|
| Рис. 5 |
Поскольку поле вне конденсатора отсутствует, т.е. поток вектора смещения через левую вертикальную часть поверхности s 1 равен нулю, то интеграл берется только по правой вертикальной части s 1, равной D s:
.
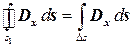Направления векторов электрического смещения D x и внешней (положительной) нормали n к поверхности s 1 на левом электроде совпадают, поэтому последнее соотношение принимает вид
,
откуда следует:
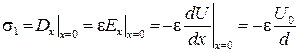, т.е. на левом электроде поверхностная плотность заряда s1 отрицательна.
Аналогичным образом охватим некоторую часть D s правого электрода замкнутой поверхностью s 2 (рис. 5, б). На правом электроде векторы D x и n направлены в противоположные стороны, следовательно, угол между ними равен p, поэтому в этом случае имеем:
.
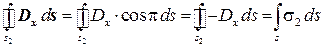Отсюда вытекает, что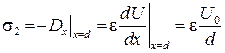 
положительна. Векторы D и E направлены от положительного заряда к отрицательному (рис. 4).
Для заданных параметров задачи U 0=220 В, d =1 см, e=3e0, s =0,01 м2 получим:
E = –22000 В/м; s1=–5,841·10–7 Кл/м2; s2=5,841·10–7 Кл/м2.
Полные заряды электродов равны:
;
.
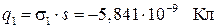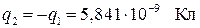1.2. При наличии объемного заряда потенциал описывается уравнением Пуассона
.
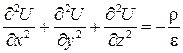Поскольку проекции Ey =0 и Ez =0, то это уравнение переходит в обыкновенное дифференциальное уравнение второго порядка:
.
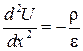Двукратное интегрирование дает:
,
.
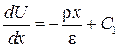Если объемный заряд вносится при подключенном источнике, то граничные условия, описанные в п. 1.1, сохраняются:
1. x =0, U =0, откуда C 2=0;
2. x = d, U = U 0.
Подстановка выражения для потенциала U (x) в это условие дает:
, откуда найдем 
.
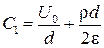Таким образом, потенциал описывается уравнением
.
Напряженность поля равна
.
На рис. 6 показаны кривые распределения потенциала и напряженности поля в конденсаторе при следующих данных:
U 0=220 В, d =1 см, e=3e0, r=2,5·10–4 Кл/м3.
Подобный характер распределения потенциала, имеющего максимум внутри области существования поля, возможен только при наличии объемно распределенного заряда в пространстве между электродами. В этом случае потенциал описывается уравнением Пуассона. При отсутствии такого заряда потенциал, описываемый уравнением Лапласа, может иметь максимумы и минимумы только на границах области (ср. рис. 4, а и рис. 6).
|
| Рис. 6 |
Следует отметить что, если на данном отрезке (x <0,0073 м) кривой U (x) потенциал возрастает, то напряженность поля имеет отрицательные значения. При убывающем потенциале (x >0,0073 м) напряженность положительна. В точке экстремума (x =0,0073 м) кривая напряженности переходит через нуль.
Поверхностные плотности зарядов электродов в этом случае определяются выражениями:
на левом электроде
;
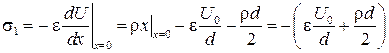на правом электроде
.
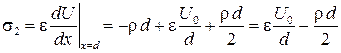Для заданных параметров задачи получим:
; 
. Нетрудно заметить, что в данном случае 
, причем обе эти величины отрицательны. Однако суммарный заряд, состоящий из поверхностных зарядов s1 и s2 и объемного r, равен нулю:
.
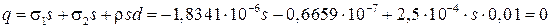Следует подчеркнуть, что емкость не может быть определена по результатам расчета этого пункта, т.к. между электродами присутствует объемный заряд, а емкость определяется только при отсутствии объемного заряда.
1.3. Рассмотрим случай, когда заряженный конденсатор с потенциалами электродов – правого U = U 0, левого U =0 отключается от источника ЭДС и затем в пространство между электродами вносится объемный заряд. В этом случае поле также описывается уравнением Пуассона, интегрирование которого дает
,
.
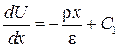Однако, для определения постоянных интегрирования необходимо использовать другие граничные условия. После отключения правого электрода от источника он оказывается окруженным диэлектриком. Поэтому при внесении объемного заряда его заряд измениться не может, т.е. поверхностная плотность заряда на нем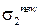 
останется равной 
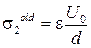, которая была до внесения заряда r (см. п. 1.1). Следовательно, граничное условие при x = d примет вид:
, или
.
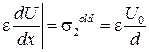На заземленном левом электроде сохранится условие U =0.
Таким образом, для определения постоянных интегрирования имеем два уравнения:
x =0,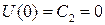 
,
x = d,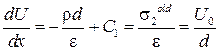 
, откуда 
.
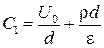Выражение для потенциала принимает вид:
,
.
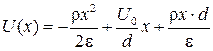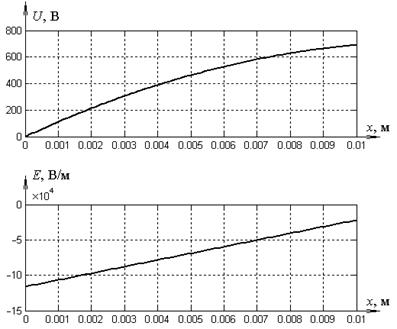
На рис. 7 показаны кривые распределения потенциала и напряженности поля в конденсаторе при следующих данных:
U 0=220 В, d =1 см, e=3e0, r=2,5·10–4 Кл/м3.
|
| Рис. 7 |
Обратим внимание на то, что в данном случае потенциал правого электрода U 2 не равен U 0:
,
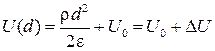где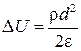 
– добавка за счет объемного заряда, внесенного после отключения источника.
Поверхностные плотности зарядов электродов равны:
;
.
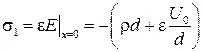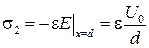При заданных параметрах задачи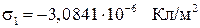 
; 
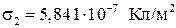. Как видно из полученных результатов, , причем в данном случае они имеют разные знаки. Однако суммарный заряд электродов равен нулю:
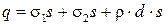= – 3,0841·10–6· s +5,8410·10–7· s +2,5·10–4·0,01· s= 0.
1.4. Расчет емкости конденсатора. Емкость конденсатора определяется при условии, что заряды электродов равны по величине и противоположны по знаку q 1=– q 2 как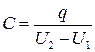 
, где q – заряд электрода. При этом берется заряд того электрода, от которого отсчитывается потенциал, т. е. в данном случае q = q 2. Подчеркнем, что емкость конденсатора определяется только при отсутствии объемного заряда между электродами. Как следует из п. 1.1,
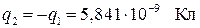. Тогда 
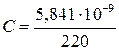= 2,655·10–11 Ф.
ПРИМЕР 2. В плоском конденсаторе (рис. 8) с двухслойным диэлектриком потенциал правого электрода равен U 0, левый электрод заземлен
|
| Рис. 8 |
Расстояние между электродами равно D. Граница раздела областей 1 и 2, заполненных диэлектриками с проницаемостями e1 и e2, расположена на расстоянии d 1 от левого электрода. Рассчитать и построить распределения потенциала и напряженности поля в пространстве между электродами при следующих параметрах задачи: U 0=220 В, d 1=1 см, D =2 см; e1=3e0, e2=2e0.
Определить, при каком значении d 1 приложенное к конденсатору напряжение делится поровну между слоями диэлектриков.
РЕШЕНИЕ
Направим ось х перпендикулярно поверхностям пластин, как показано на рис. 8. Примем условие, что размеры электродов конденсатора значительно больше расстояния между ними. В этом случае можно не учитывать эффекты вблизи краев электродов. Это позволяет считать, что в пространстве между ними вектор напряженности поля направлен вдоль оси х, а его величина зависит только от х: E = f (x). Уравнение Лапласа в декартовой системе координат имеет вид:
.
В рассматриваемой задаче проекции Ey =0 и Ez =0. Поэтому уравнение Лапласа переходит в обыкновенное дифференциальное уравнение второго порядка:
.
Поскольку диэлектрические проницаемости областей различны, необходимо рассматривать отдельно потенциалы в каждой из областей. Для первой области 0< x < d 1 имеем
.
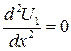Выполнив двукратное интегрирование по х, получим решение в виде:
,
.
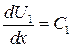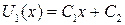Аналогично для второй области d 1< x < D имеем уравнение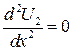 
, и после двукратного интегрирования получим
;
.
Составим четыре уравнения для определения четырех постоянных интегрирования (С 1, С 2, С 3, С 4), используя граничные условия:
1. При х =0 по условию задачи U 1=0. Подставив это условие в выражение для U 1(x), получаем С 2=0.
2. При х = D потенциал U 2= U 0. Подставив это значение в соотношение для U 2(x), найдем:
.
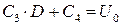3. При х = d 1из условия равенства потенциалов U 1= U 2 получим:
.
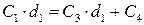4. При х = d 1 условие равенства нормальных составляющих вектора смещения можно записать в виде: 
. Подставляя это условие в выражения для производных U 1(x) и U 2(x), придем к соотношению:
.
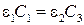Решая совместно полученные уравнения, находим значения постоянных С 1, С 3, С 4:
; 
; 
,
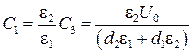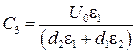где обозначено d 2= D – d 1.
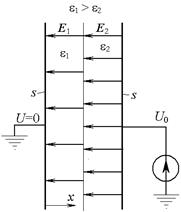
При заданных числовых значениях U 0=220 В, d 1= d 2= D /2=0,01м, e1=3e0; e2 =2e0 получим: C 1=8800 В/м; C 3=13200 В/м; C 4=–44 В. Распределение потенциала показано на рис. 9, а.
а)
| б)
|
| Рис. 9 |
Распределение напряженности электрического поля в 1-й области определяется выражением:
.
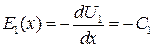Во 2-й области имеем:
.
Отсюда следует, что напряженность поля не зависит от координаты x, при этом вектор напряженности направлен против координаты x от электрода с большим потенциалом в сторону электрода с меньшим потенциалом (рис. 9, б).
Определим теперь значение d 1, при котором напряжение делится поровну между слоями диэлектрика. Выполним расчет численно. Будем рассчитывать величину потенциала на границе раздела слоев диэлектрика при различных значениях d 1.
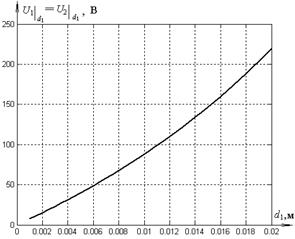
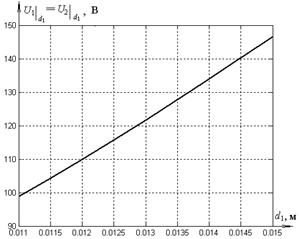
На рис. 10, а представлена зависимость величины потенциала на границе раздела сред от d 1. Видно, что напряжение между электродами делится поровну между слоями диэлектрика при значениях d 1, лежащих в окрестности 0,012 м. Для уточнения результата проведем аналогичные вычисления с более мелким шагом в окрестности этой точки (рис. 10, б).
а)
| б)
|
| Рис. 10 |
Уточненный расчет показывает, что напряжение между электродами конденсатора делится пополам при d 1=0,012 м.
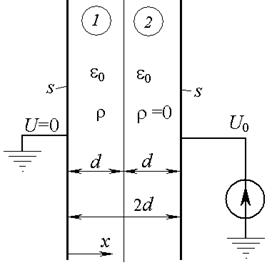
ПРИМЕР 3. В плоском конденсаторе (рис. 11) с воздушной изоляцией около левого электрода распределен объемный заряд с плотностью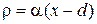 
, где х отсчитывается от левого электрода.
|
| Рис. 11 |
Границей объемного заряда является плоскость, параллельная пластинам электродов конденсатора. Расстояние между границей области заряда и левым электродом равно d. Расстояние между электродами равно 2 d. Левый электрод заземлен (имеет нулевой потенциал). Правый электрод имеет потенциал U 0. Найти распределение потенциала и напряженности поля в пространстве между электродами конденсатора и построить графики. Построить распределение потенциала и напряженности в конденсаторе, поменяв полярность электродов.
Задачу решить при U 0=220В, d =1 см,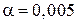 
Кл/м4.
РЕШЕНИЕ
Предположим, что размеры электродов конденсатора значительно больше расстояния между ними.
Направим ось х перпендикулярно поверхностям пластин, как показано на рис. 11. Считаем, что вектор напряженности поля направлен вдоль оси х, а его величина зависит только от х. Уравнение Пуассона в декартовой системе координат имеет вид:
.
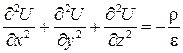В рассматриваемой задаче проекции Ey =0 и Ez =0. Поэтому уравнение Пуассона переходит в обыкновенное дифференциальное уравнение второго порядка:
.
Производим двукратное интегрирование по х и получим решение для области с объемным зарядом (0< x < d):
,
.
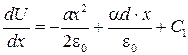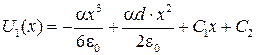Для расчета потенциала в области без объемного заряда (d < x <2 d) решаем уравнение Лапласа:
.
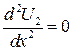Его решение имеет вид:
,
.
Составим четыре уравнения для определения четырех постоянных интегрирования (С 1, С 2, С 3, С 4), используя граничные условия:
При х =0 U =0. Подставляя это условие в решение уравнения Пуассона для 1-й области, получаем С 2=0.
При х =2 d U = U 0. Подставляем это условие в решение уравнения Лапласа для 2-й области:
. (*)
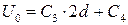При х = d имеем U 1= U 2:
. (**)
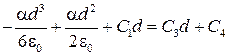При х = d имеем .
Подставляем это условие в производные решений:
. (***)
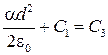Решая совместно уравнения (*), (**) и (***), относительно С 1, С 3, С 4, находим значения постоянных интегрирования. При заданных числовых значениях U 0, d,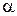 
получим С 1 = –1,25∙104 В/м, С 3 = 1,57∙104 В/м, С 4 = –94 В.
Распределение напряженности электрического поля в 1-й области:
.
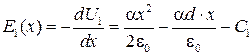Во 2-й области:
= 1,57∙104 В/м.
Графики зависимостей U (x) и E (x) изображены на рис. 12, кривые 1.
Решим задачу, изменив полярность электродов конденсатора на противоположную: потенциал правого электрода примет значение U 2= – U 0= –220 В, потенциал левого электрода останется равным нулю. В этом случае изменится одно из граничных условий: при х =2 d U =– U 0, и, следовательно, изменятся значения постоянных: С 1=–3,45∙104 В/м, С 3=–0,627∙104 В/м, С 4 =–94 В.
Графики зависимостей U (x) и E (x) при обратной полярности напряжения на электродах конденсатора также изображены на рис. 12, кривые 2.
Сравнив кривые E (x) для об