Математический анализ.
Здравствуйте! В этой лекции Вы продолжите рассмотрение раздела «Математический анализ» изучением интегрального исчисления вы познакомитесь с понятием неопределённого интеграла, его свойствами, методами вычисления. Желаем Вам успехов в изучении этой темы.
Первообразная и неопределённый интеграл
В математике, как и в её приложениях, часто возникает задача, обратная к той, которая решалась в дифференциальном исчислении, а именно: дана функция  , найти функцию
, найти функцию 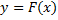 , такую, что
, такую, что 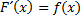 .
.
Например: Динамика формирования оборотных средств – это процесс изменения во времени, который можно рассматривать как непрерывный. Пусть 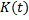 – это зависимость оборотных средств, которую можно рассматривать так же, как скорость потока денежных средств
– это зависимость оборотных средств, которую можно рассматривать так же, как скорость потока денежных средств  .
.
Если нам дана функция скорости потока, то возникает задача нахождения функции оборотных средств, которая сводится к операции нахождения функции по её производной.
Такая операция называется интегрированием, а раздел математики, изучающий методы нахождения функции по её производной, - интегральным исчислением.
Одним из главных понятий интегрального исчисления является понятие первообразной.
Определение. Функция 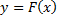 называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке
на промежутке 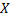 , если в любой точке этого промежутка выполняется равенство.
, если в любой точке этого промежутка выполняется равенство. 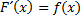 .
.
Надо отметить. Что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число 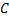 , так как
, так как 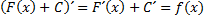 . следовательно, для отыскания всех первообразных функции для функции
. следовательно, для отыскания всех первообразных функции для функции  достаточно найти какую-нибудь одну, все остальные получаются добавлением всевозможных констант.
достаточно найти какую-нибудь одну, все остальные получаются добавлением всевозможных констант.
В силу этого выражение  , где
, где 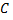 - произвольная константа, а
- произвольная константа, а 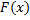 - какая-то первообразная для функции
- какая-то первообразная для функции  , представляет собой общий вид функции, которая имеет производную
, представляет собой общий вид функции, которая имеет производную  . это выражение называется неопределённым интегралом от функции
. это выражение называется неопределённым интегралом от функции  от функции
от функции  и обозначается.
и обозначается. 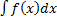 . (Читается: «эф от икс по дэ от икс»).
. (Читается: «эф от икс по дэ от икс»).
Определение. Неопределённым интегралом функции  называется совокупность первообразных функции, которые определены соотношением:
называется совокупность первообразных функции, которые определены соотношением:
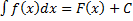 . (1)
. (1)
В этом случае  – подынтегральная функция,
– подынтегральная функция, 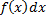 – подынтегральное выражение.
– подынтегральное выражение.
Условием существования неопределённого интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства неопределённого интеграла
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е.
(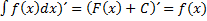 .
.
2. Постоянный множитель можно выносить за знак интеграла, т.е. 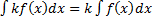 .
.
3. Неопредёлённый интеграл сумы (разности) нескольких функций, равен сумме (разности) интегралов слагаемых функций, т.е. 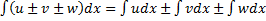 ;
;
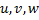 – некоторые функции от
– некоторые функции от  .
.
4. Неопределённый интеграл от производной функции равен совокупности таких функций, т.е. 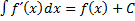 .рассмотрим пример вычисления интеграла:
.рассмотрим пример вычисления интеграла:
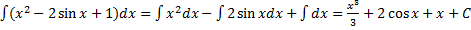 .
.
При нахождении этого интеграла применили все свойства, о которых только говорили. Т.е., подынтегральная функция представляет собой алгебраическую сумму, значит, интеграл можно разбить по третьему свойству на алгебраическую сумму интегралов. Теперь о каждом из интегралов в отдельности. Интеграл вида 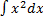 по определению неопределённого интеграла и формуле(1) будет равен
по определению неопределённого интеграла и формуле(1) будет равен 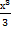 , т.к.
, т.к.  . Таким образом, ещё раз подчеркнём, что интегрирование – действие, обратное дифференцированию. Значит. Необходимо хорошо знать таблицу производных из второй лекции. Так как, мы должны найти такую совокупность первообразных, производная которой равна подынтегральной функции.
. Таким образом, ещё раз подчеркнём, что интегрирование – действие, обратное дифференцированию. Значит. Необходимо хорошо знать таблицу производных из второй лекции. Так как, мы должны найти такую совокупность первообразных, производная которой равна подынтегральной функции.
Далее интегрируем 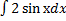 , рассуждая аналогично предыдущему. Что сразу замечаем? А то, что под знаком интеграла есть постоянный множитель, т.е. число 2, которое можно вынести за знак интеграла по второму свойству. А по поводу
, рассуждая аналогично предыдущему. Что сразу замечаем? А то, что под знаком интеграла есть постоянный множитель, т.е. число 2, которое можно вынести за знак интеграла по второму свойству. А по поводу 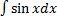 следует сказать так, что он равен такой совокупности первообразных, производная от которой равна
следует сказать так, что он равен такой совокупности первообразных, производная от которой равна 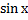 . А значит,
. А значит,  , так как
, так как 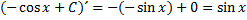 .
.
Приступая к интегрированию выражения 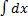 , найдём такую совокупность первообразных, производная которой равна подынтегральной функции, т.е. единице. А значит,
, найдём такую совокупность первообразных, производная которой равна подынтегральной функции, т.е. единице. А значит, 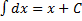 , так как
, так как 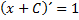
Следует заметить, что при вычислении каждого из интегралов, мы получали первообразную и плюс константу С. так как в рассматриваемом примере была сумма трёх интегралов, то должны были получиться три постоянные в ответе. Но рассуждаем так, что сумма постоянных есть снова число постоянное, и в ответе мы записываем только одну константу. Поэтому при устных рассуждениях говорят, что в процессе интегрирования алгебраической суммы в ответе записывают только одну константу.
Резюмируя все рассуждения, получим то, что записано в решении этого примера.
Итак, нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределённых интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределённых интегралов большинство элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объёмными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведём таблицу основных интегралов, с помощью которой можно получить значения неопределённых интегралов различных функций.
| № | Интеграл | Значение | № | Интеграл | Значение |
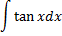
| 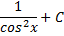
| 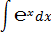
| 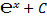
| ||
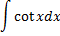
| 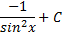
| 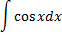
| 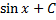
| ||

| 
| 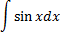
| 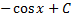
| ||
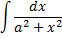
| 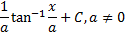
| 
| 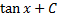
| ||
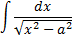
| 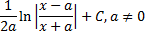
| 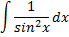
| 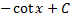
| ||

| 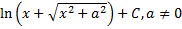
| 
| 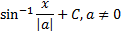
| ||
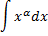
| 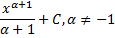
| 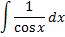
| 
| ||
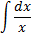
| 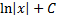
| 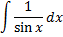
| 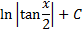
| ||
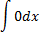
| 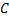
| 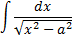
| 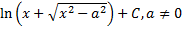
|
Методы интегрирования
Рассмотрим три основных метода интегрирования: метод непосредственного интегрирования, интегрирование методом замены переменной (подстановки) и интегрирование по частям.
А теперь более подробно остановимся на каждом из названных методов интегрирования.
Непосредственное интегрирование
Интегрирование, основанное на применении свойств интеграла. Называют непосредственным или интегрированием методом разложения.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием.
Таким образом, ещё раз заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 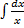 . На основе известной формулы дифференцирования (
. На основе известной формулы дифференцирования (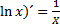 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 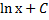 , где
, где 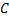 – некоторое постоянное число. Однако, с другой стороны (
– некоторое постоянное число. Однако, с другой стороны (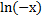 )´ =
)´ = 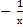
 (
(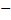 1) =
1) =  . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод: 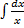 =
= 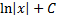
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались чёткие приёмы и методы, правила нахождения производной, наконец, определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определённых правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знание таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
В качестве примера рассмотри интеграл вида 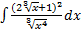 . Что сразу видим? Да конечно же то, что интеграл в таком виде не является табличным и его пока нельзя взять с помощью рассмотренных свойств. А как же быть? Да, видимо вы уже заметили, что в числителе дроби записана формула квадрата суммы двучлена, которую мы и раскроем. Тогда получим, что
. Что сразу видим? Да конечно же то, что интеграл в таком виде не является табличным и его пока нельзя взять с помощью рассмотренных свойств. А как же быть? Да, видимо вы уже заметили, что в числителе дроби записана формула квадрата суммы двучлена, которую мы и раскроем. Тогда получим, что 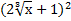 = 4
= 4 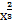 + 4
+ 4 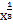 +1. По отношению к знаменателю следует заметить, что лучше его представить в виде
+1. По отношению к знаменателю следует заметить, что лучше его представить в виде 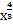 . Если подставим все преобразованные функции под знак интеграла, то в результате получим интеграл в виде
. Если подставим все преобразованные функции под знак интеграла, то в результате получим интеграл в виде 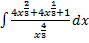 . Если проанализировать всё то, что мы уже знаем о неопределённом интеграле, то там ничего не говорится об интеграле частного. И, кроме того, этот интеграл не является табличным. Итак, мы не можем брать интеграл частного. Произведения, а можем брать интеграл алгебраической суммы в соответствии со свойством 3. Значит, напрашивается вывод – перейти к алгебраической сумме. В нашем случае этого можно достичь, выполнив почленное деление,(каждое слагаемое числителя делится на знаменатель), и, произведя действия с показателями степеней с одинаковыми основаниями показатели степеней вычитаются), в итоге получаем
. Если проанализировать всё то, что мы уже знаем о неопределённом интеграле, то там ничего не говорится об интеграле частного. И, кроме того, этот интеграл не является табличным. Итак, мы не можем брать интеграл частного. Произведения, а можем брать интеграл алгебраической суммы в соответствии со свойством 3. Значит, напрашивается вывод – перейти к алгебраической сумме. В нашем случае этого можно достичь, выполнив почленное деление,(каждое слагаемое числителя делится на знаменатель), и, произведя действия с показателями степеней с одинаковыми основаниями показатели степеней вычитаются), в итоге получаем
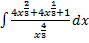 =
= 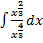 +
+ 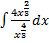 +
+ 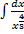 = 4
= 4  + 4
+ 4 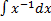 +
+  = 12
= 12 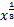 + 4
+ 4 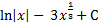 .
.
Для окончательного интегрирования мы воспользовались формулой (7) для первого и третьего интегралов и формулой (8) для второго интеграла.
Что ещё следует заметить по поводу непосредственного интегрирования. Да, в этом примере метод интегрирования называют непосредственным, хотя пришли мы к нему через применение свойств и правил элементарной математики.
На следующем примере снова покажем работу этого метода.
Пример. 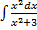 . интеграл не является табличным и пока невозможно выполнить почленное деление, нет алгебраической суммы в числителе. Но по свойствам элементарной математики мы можем в числителе прибавить и вычесть число три, а потом выполнить почленное деление, т.е.
. интеграл не является табличным и пока невозможно выполнить почленное деление, нет алгебраической суммы в числителе. Но по свойствам элементарной математики мы можем в числителе прибавить и вычесть число три, а потом выполнить почленное деление, т.е. 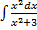 =
=  =
= 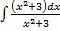 -
-  =
= 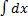 - 3
- 3  .
.
Легко заметить, что первый интеграл равен 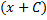 , так как (
, так как ( )´ = 1, а второй интеграл является табличным (формула(4), если представить 3 =
)´ = 1, а второй интеграл является табличным (формула(4), если представить 3 = 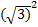 ).
).
В реультате получаем
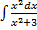 =
= 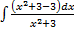 -
-  =
= 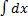 - 3
- 3  = x
= x 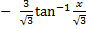 +
+ 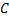 = x -
= x -  +
+ 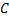 .
.
Рассмотрим следующий метод интегрирования.
Способ подстановки (замены переменных)
В основе метода подстановки (или метода замены переменной) вычисления неопределённых интегралов лежит следующая формула, являющаяся простым следствием правила дифференцирования сложной функции
 = F(g(x)) +
= F(g(x)) + 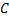 , о котором мы вели речь во второй лекции.
, о котором мы вели речь во второй лекции.
Найдём неопределенный интеграл вида 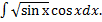
И снова подынтегральная функция представляет собой произведение, а значит, непосредственно брать интеграл нельзя. Сделаем замену, обозначив 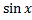 = t, затем, продифференцировав обе части этого равенства получим
= t, затем, продифференцировав обе части этого равенства получим  =
=  . Возвратившись к исходному интегралу, записали его в новых переменных, полученный интеграл оказался табличным, и взяли его с помощью формулы (7) из первой таблицы. Но затем в ответе снова перешли к прежней переменной, возвратившись к подстановке. Все наши рассуждения мы оформили в решении с использованием вертикальных скобок, кстати, можно брать фигурные скобки, т.е., это право автора.
. Возвратившись к исходному интегралу, записали его в новых переменных, полученный интеграл оказался табличным, и взяли его с помощью формулы (7) из первой таблицы. Но затем в ответе снова перешли к прежней переменной, возвратившись к подстановке. Все наши рассуждения мы оформили в решении с использованием вертикальных скобок, кстати, можно брать фигурные скобки, т.е., это право автора.
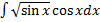 =
= 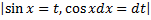 =
= 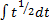 =
= 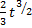 +
+ 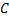 =
=  +
+ 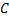 .
.
Или следующий пример: вычислить интеграл  . Сделаем замену:
. Сделаем замену: 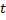 =
= 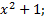
 =2
=2 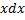 ;
; 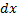 =
= 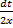 . Получаем:
. Получаем: 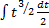 =
= 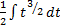 =
= 

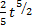 + C =
+ C =  +
+ 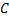 =
= 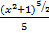 +
+ 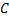 ;
;
Следует обратить внимание, что мы выражаем из результата дифференцирования подстановки, имеющиеся в условии интеграла выражение 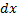 , а в других случаях это будет некоторое другое выражение. Рассмотрим интеграл вида
, а в других случаях это будет некоторое другое выражение. Рассмотрим интеграл вида 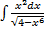 =
= 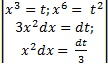 =
= 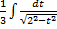 =
=  .
.
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций. Но сформулируем общее правило метода подстановки, которое вытекает из практического опыта.
1. Вводят походящую подстановку (это означает, что нужно устно «прикинуть», что даст результат её дифференцирования).
2. Дифференцируют обе части подстановки.
3. Выражают из результата дифференцирования имеющееся подынтегральное выражение в условии интеграла.
4. Получив интеграл в новых переменных, решают его с помощью формул (например из таблицы 1)
5. Затем, возвратившись к подстановке, записывают ответ в исходных переменных.
Кроме рассмотренных двух методов широко используется в интегральных исчислениях и метод интегрирования по частям, о котором мы будем сейчас вести речь.
Интегрирование по частям.
Этот способ основан на известной формуле производной произведения: 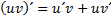 , где
, где 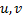 - некоторые функции от
- некоторые функции от 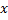 . В дифференциальной форме:
. В дифференциальной форме: 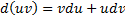 . Поэтому
. Поэтому 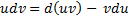 . Интегрируя обе части этого равенства, получим
. Интегрируя обе части этого равенства, получим 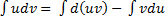 . Используя свойство неопределённых интегралов
. Используя свойство неопределённых интегралов 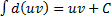 , получим формулу
, получим формулу
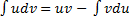 . (2)
. (2)
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.  .
.
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл табличному. Естественно, возникает вопрос: «Что обозначать за  , а что за
, а что за 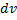 ?» ответ, на который такой: - «То, что позволит
?» ответ, на который такой: - «То, что позволит