ПЛОСКОСТЬ
1. Найти уравнение плоскости, проходящей через точку M(4, 1, 5) перпендикулярно вектору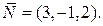 
Для решения этой задачи возьмем уравнение плоскости, проходящей через точку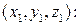 
Здесь А, В, С – координаты вектора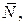 
который перпендикулярен этой плоскости. Вначале подставим в уравнение координаты точки М:
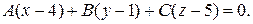
Затем - компоненты нормального вектора и получим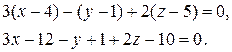 
Ответ: 3x-y+2z-21=0.
2. Найти угол между двумя плоскостями
3x+2y+z-7=0, x+4y-3z+2=0.
Угол между плоскостями равен углу между перпендикулярами к ним. Нормальные векторы этих плоскостей 
По формуле
найдем
Так как правая часть положительная, то угол между плоскостями острый.
3. Найти расстояние от точки М(5, 1,-2) до плоскости
3x+2y-4z +1=0. Оно определяется по формуле как
В нашем случае
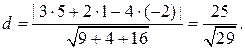
4. Найти уравнение плоскости, проходящей через точку
M(2,-3, 5) параллельно плоскости 4x-y+2z-7=0.
Снова возьмем уравнение плоскости, проходящей через точку, и подставим туда координаты т. М:
A(x-2)+B(y+3)+C(z-5)=0.
Так как обе плоскости параллельны, то они имеют один и тот же нормальный вектор 
Тогда для данного случая 4(x-2)-(y+3)+2(z-5)=0 или
4x-y+2z-21=0.
5. Найти уравнение плоскости, проходящей через 3 точки K(3,0,-1), L(2,1,5), P(4,2,0).
Возьмем еще точку M(x,y,z), также лежащую в этой плоскости. У нас будет 3 компланарных вектора:
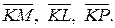Их смешанное произведение будет равно нулю 
Это можно записать в виде уравнения
Упрощая последнее равенство, получим:
11x-7y+3z-30=0.
6. Найти уравнение плоскости, проходящей через точки
K(2, -5, 0), L(6, 0,2) перпендикулярно плоскости
x+5y+2z-10=0.
Здесь также ищем 3 компланарных вектора:
Уравнение примет вид
Из последнего выражения получим ответ:
2y-5z+10=0.
7. Записать уравнения прямой 
в параметрическом виде.
Канонические уравнения прямой имеют вид: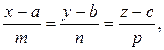 
где a,b,c – координаты точки, через которую прямая проходит, а m,n,p – компоненты вектора, параллельного данной прямой. В нашем примере мы правую часть приравняли параметру t.
Из равенства каждой дроби t получим:
x-3=2t, y+1=4t, z+6=5t.
Отсюда придем к параметрическим уравнениям прямой: x=2t+3, y=4t-1, z=5t-6.
Обратная задача решается исключением параметра t.
8. Привести общее уравнение прямой
3x+2y-z-7=0,
4x-y+3z-2=0
к каноническому виду. Здесь прямая рассматривается как линия пересечения двух плоскостей. Предположим, что наша прямая пересекает плоскость ХУ. Тогда z=0 и система примет вид
3x+2y=7,
4x-y=2.
Решением системы будет x=1, y=2. Следовательно,
точкой прямой будет (1,2,0).
Вектор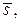 
параллельный нашей прямой, определится
как векторное произведение векторов
Следовательно,
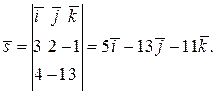
Канонические уравнения прямой можем записать как 
9. Найти канонические уравнения прямой, проходящей через две точки K(5, -2, 1) и L(4, 3, 7).
Здесь уравнения в общем случае имеют вид:
Подставим сюда координаты этих точек. Тогда
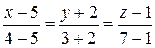
и окончательно получим
10. Найти угол между двумя прямыми
Его найдем как угол между векторами 
Тогда
11.Через точку (3, -1,4) провести прямую, параллельную прямой
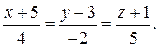
В канонические уравнения подставим вначале координаты точки:
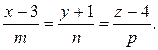
Так как прямые параллельны, то направляющие векторы у них совпадают и в итоге получим:
12. Найти точку пересечения прямой
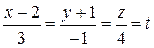
и плоскости 2x-y+5z-32=0.
Запишем параметрические уравнения прямой как
x=3t+2, y=-t-1, z=4t.
Подставим эти x, y, z в уравнение плоскости и получим 2(3t+2)-(-t-1)+5*4t-32=0. Отсюда найдем, что
t=1 и x=5, y=-2, z=4.
13. Найти угол между прямой
и плоскостью 3x-y+z-22=0.
Здесь направляющий вектор прямой 
и
нормальный вектор плоскости 
Угол найдем по формуле
14. Определить уравнение плоскости, которая проходит через точку K (3, 1, -2) и через прямую
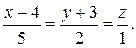
Эту задачу можно решать тремя способами. Мы будем искать 3 компланарных вектора. Возьмем точку плоскости M(x,y,z) с текущими координами. Точка прямой L(4,-3,0) также лежит в плоскости. Имеем 3 компланарных вектора
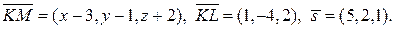
Их смешанное произведение равно нулю. Тогда
Раскрывая этот определитель по первой строке, в итоге получим уравнение плоскости
8x-9y-22z-59=0.