2.1. Термодинамическая параметризация физических систем.
Состояние термодинамической системы в общем виде описывается обобщенным уравнением, характеризующим процесс изменения физической величины Y, имеющей поле с потенциалом φ Y в среде со свойством ξ Y:
 ,
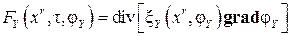| (2.1) |
где xr – система координат;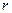 
= 1, 2, …, R; R – число пространственных измерений (далее рассматривается одномерная задача); FY – функция процесса. В краевой постановке его решением является распределение потенциала в зависимости от координаты и времени при определенных краевых условиях:
 .
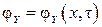| (2.2) |
Начальные условия определяют значение искомой функции или ее производной в момент времени τ = 0:
 ,
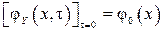| (2.3) |
 .
| (2.4) |
Краевые условия задают значения искомой функции или ее производной на границах среды, в пределах которой определяется функция потенциала:
1. первого рода, когда задается граничное значение функции
  ;
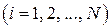| (2.5) |
2. второго рода, когда задается граничное значение первой производной функции
 ,
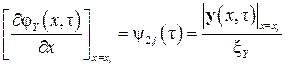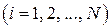| (2.6) |
где y – плотность потока величины Y;
3. третьего рода, когда задается граничное значение линейной комбинации функции и ее первой производной
 ,
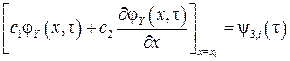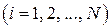| (2.7) |
где с 1 = const; c 2 = const.
Функция процесса первого порядка по времени, характеризуемого величиной Y, представляется в виде
 ,
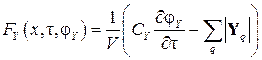| (2.8) |
где СY – емкость системы по отношению к величине Y (способность системы накапливать величину Y в объеме V); Y q – потоки величины Y, направленные в систему и из нее. Знак потока следует из противоположной направленности векторов потока и градиента потенциала: при положительном градиенте потенциала в уравнении (2.1) поток отрицателен.
2.2. Идентификация математических моделей.
Пусть открытая система состоит из N элементов, закон взаимодействия которых выражается через степень D потенциала φ Y:
 ,
| (2.9) |
где α D,ik – коэффициенты взаимодействия. Тогда функция процесса, связанного с величиной Y, для элемента i выражается как
 ,
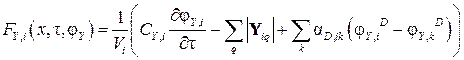| (2.10) |
а обобщенное уравнение (2.1) записывается в виде
 ,
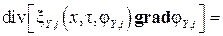
| (2.11) |
Состояние совокупности N элементов описывается системой уравнений
 .
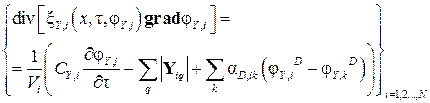| (2.12) |
Если распределение потенциала внутри элементов считается равномерным, производные по координате равны нулю, и уравнения упрощаются до вида МСП:
 .
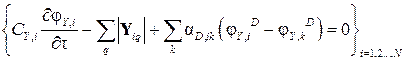| (2.13) |
Прямая задача заключается в определении поля φ Y при известных СY,i ,, | Y iq |, α D,ik. и начальных условиях, обратная – в определении СY,i ,, | Y iq | или α D,ik по полю φ Y. Обратная задача идентификации коэффициентов взаимодействия для связей степени D сводится к решению системы уравнений (2.13) относительно α D,ik:
 .
| (2.14) |
Если узел i имеет одну единственную связь α D , ik, то при отсутствии потоков | Y ik | и известной емкости СY,i коэффициент взаимодействия узла i c узлом k восстанавливается по полю потенциала и его первой производной по времени:
  .
| (2.15) |
Наличие экспериментально измеренных производных в правой части уравнений (2.15) может быть причиной больших колебаний решения α D , ik при малых изменениях исходных данных φ Y,I или, иными словами, плохой обусловленности обратной задачи.