Расчёт балки методом конечных элементов

с использованием программы Mathcad.

Задание: Построить эпюры внутренних изгибающих моментов и поперечных сил, а также эпюру прогибов балки.

 

Сформируем расчётную конечно-элементную модель балки из трёх конечных элементов (и четырёх узлов):

 

Количество степеней свободы в каждом узле примем равное двум:

1) возможность перемещаться перпендикулярно оси балки,

2) возможность поворота в плоскости расчётной схемы,

и установим для них следующее правило знаков:

1) вертикальное перемещение (прогиб), положительное направление – вниз,

2) угол поворота, положительное направление – по часовой стрелке.

Таким образом, примем и зададим в программе Mathcad:

- количество степеней свободы одного конечного элемента: Ne: = 4,

 

 

- количество степеней свободы всей расчётной модели балки: Ns: = 8.

1. Исходные данные:

 

Жёсткость балки при изгибе: EI = 100000 (кН∙м²)

 

Параметры нагрузки: q = 2 (кН/м), Р = 9 (кН), М = 6 (кН∙м),

 

Длины конечных элементов: L1 = 4 (м), L2 = 2 (м), L3 = 2 (м)

 

Зададим на Mathcad: EI:= 100000 q: = 2 Р: = 9 М: = 6

 

Номер первого элемента в каждом массиве, используемом в программе, зададим равным единице:

ORIGIN:= 1

 

(по умолчанию Mathcad назначил бы номер первого элемента каждого используемого в программе массива равным нулю).

2. Формирование матрицы жёсткости расчётной модели.

Сформируем локальные матрицы жёсткости трёх конечных элементов К1, К2, К3:

Запишем на Mathcad общее выражение матрицы жёсткости балочного конечного элемента с двумя степенями свободы в узле, c изгибной жёсткостью EI и длиной L. Для построения матриц и векторов будем использовать опцию «Матрица» на Панели инструментов Mathcad:

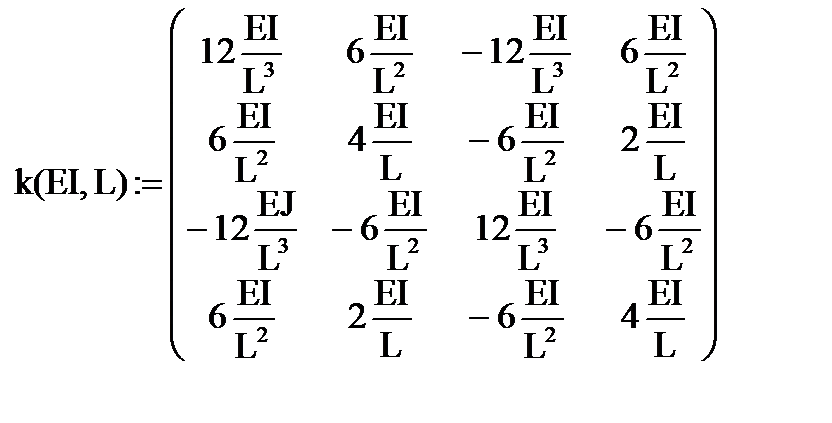
Построим матрицу жёсткости конечного элемента № 1 с изгибной жёсткостьюEI = 100000 и длиной L1 = 4 (для задания степени числа можно пользоваться опцией «Калькулятор» на Панели инструментов Mathcad):

K1:= K(10⁵,L1)

Чтобы увидеть вычисленные элементы матрицы К1, напишем в программе: K1 =

 

Построим матрицу жёсткости конечного элемента № 2 с изгибной жёсткостьюEI = 100000 и длиной L2 = 2:

K2:= K(10⁵,L2)

Посмотрим на вычисленные значения элементов матрицы K2: K2 =

 

Матрица жёсткости конечного элемента № 3: K3:= K(10⁵,L3) K3 =

Теперь сформируем глобальную матрицу жёсткости расчётной модели балки в единой (глобальной) системе координат. Сначала установим соответствие локальных номеров степеней свободы конечных элементов (по четыре в каждом конечном элементе) с глобальной нумерацией степеней свободы расчётной модели. Сделаем это с помощью формируемых векторов топологии А1, А2, А3, которые будут содержать по четыре глобальных номера степеней свободы 1-го, 2-го и 3-го конечных элементов, а также с помощью т.н. матриц положения (аллокации) конечных элементов С1, С2, С3:

Векторы топологии:

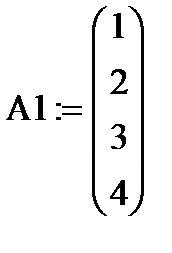A2:= A1 + 2 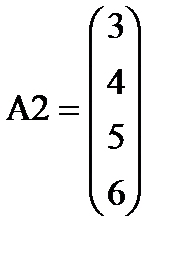A3:= A2 + 2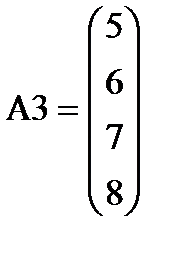

Формирование матриц положения конечных элементов:

С1_Ne,Ns:= 0 C2:= C1 C3:= C1 C4:= C1

 

Цикл по количеству степеней свободы в элементе Ne (знак операции цикла «.. » находится на Панели инструментов Mathcad в опции «Матрица», а нижние индексы, здесь обозначающие номера элементов массивов, можно ставить с помощью клавиши «[» (открывающая квадратная скобка) или клавишей «.» (точка)):

i:= 1.. Ne

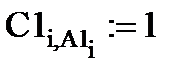
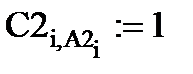
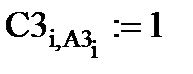
С помощью матриц положения разместим локальные матрицы жёсткости конечных элементов в поле общей (глобальной) матрицы жёсткости балки в соответствии с глобальной нумерацией их степеней свободы:

Матрица жёсткости 1-го конечного элемента на поле глобальной матрицы жёсткости:

K1g:= C1^Т × К1 × C1

(знак транспонирования матрицы берём из опции «Матрица» Панели инструментов Mathcad).

Посмотрим, как выглядит вычисленная матрица K1g: K1g =

 

 

Матрица жёсткости 2-го конечного элемента на поле глобальной матрицы жёсткости:

K2g:= C2^Т × К2 × C2 K2g =

Матрица жёсткости 3-го конечного элемента:

K3g:= C3^Т × К3 × C3 K3g =

Построим глобальную матрицу жёсткости балки K сложением локальных матриц жёсткости конечных элементов:

К:= K1g + K2g + K3g

Посмотрим на вычисленную матрицу К: К =

3. Сформируем вектор правой части F (вектор нагрузки) системы уравнений равновесия метода перемещений K∙U = F:

Сначала построим вектор заданных внешних узловых усилий Fp (с учётом принятого вначале правила знаков): сосредоточенной силы Р = 9 (кН), действующей вдоль 3-й степени свободы расчётной модели балки, и изгибающего момента М = 6 (кН∙м), действующего по 8-й степени свободы расчётной модели:

 

 

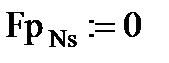
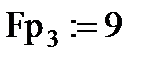
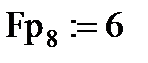посмотрим на вектор: Fp =

 

 

q

Теперь построим вектор Fq узловых равнодействующих от заданной распределённой нагрузки q = 2 (кН/м). Общий вид вектора узловых равнодействующих равномерно распределённой нагрузки интенсивностью q на балочном конечном элементе длиной L:

 

L

 

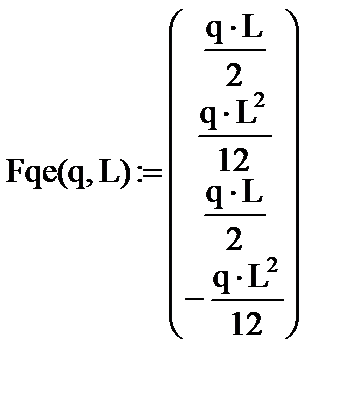
Будем использовать его для приведения нагрузки, распределённой на 2 и 3 конечных элементах, к узловым степеням свободы.

Узловые равнодействующие от распределённой нагрузки на 2-м конечном элементе:

 

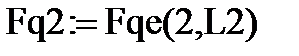
на поле глобального вектора нагрузки: Fq2g:= C2^Т ∙ Fq2

 

 

Узловые равнодействующие от распределённой нагрузки на 3-м конечном элементе:

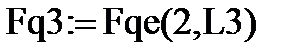
на поле глобального вектора нагрузки:

Fq3g:= C3^Т ∙ Fq3

Узловые равнодействующие от распределённой нагрузки, действующей на балку:

Fq:= Fq2g + Fq3g

Суммарный вектор нагрузки:

F:= Fp + Fq

4. Формирование и решение системы уравнений равновесия метода перемещений K∙U = F:

Определим и отметим в программе незакреплённые степени свободы балки, в направлении которых будем вычислять узловые перемещения:

u2:= 0 u3:= 0 u4:= 0 u6:= 0 u7 = 0 u8 = 0

Теперь отметим в программе закреплённые степени свободы балки, в направлении которых будем вычислять опорные реакции:

R1:= 0 R5:= 0

Построим и решим систему линейных уравнений для вычисления перемещений узлов балки в направлениях свободных степеней свободы и для выявления опорных реакций – в направлении закреплённых степеней свободы:

Given

В матричной записи системы уравнений K∙U = F + R следовало поставить знак тождества из опции «Булева алгебра» на Панели инструментов Mathcad.

Решение системы уравнений – вектор узловых перемещений в направлении степеней свободы расчётной модели балки (в м, рад):

Реакции в опорах:

5. Вычисление узловых значений внутренних усилий (поперечных сил и изгибающих моментов):

Направления усилий в крайних узловых (левом и правом) сечениях конечных элементов определены в соответствии с принятыми вначале правилами знаков. Но при этом, выбирая знаки внутренних усилий при построении их эпюр, будем руководствоваться правилами знаков строительной механики (см. рисунок):

- поперечные силы, «вращающие» элемент по часовой стрелке – положительные;

- изгибающие моменты, растягивающие нижние волокна элемента – положительные.

Правила знаков строительной механики (положительные направления):

Конечный элемент № 1 (узлы с номерами 1 и 2)

Перемещения в узлах 1-го конечного элемента (м):

U1:= C1×U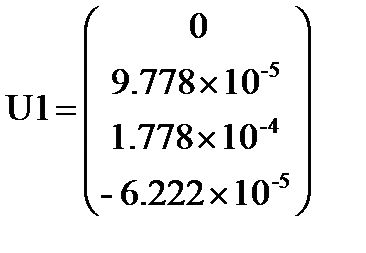

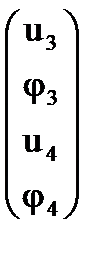
Здесь u_i – прогиб балки (м) в i – ом узле, φ_i – угол поворота оси балки (рад) в i – ом узле.

Внутренние усилия в узлах 1-го конечного элемента (кН, кН∙м):

S1:= K1×U1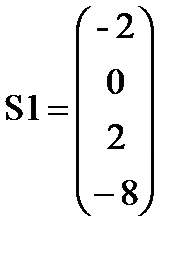

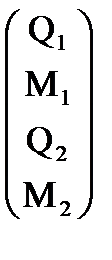
Конечный элемент № 2 (узлы с номерами 2 и 3)

Перемещения в узлах 2-го конечного элемента (м, рад):

U2:= C2×U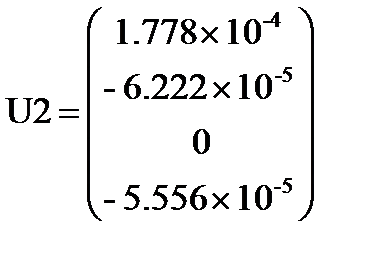

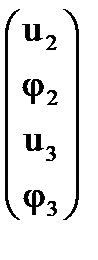
Внутренние усилия в узлах 2-го конечного элемента (кН, кН∙м):

S2:= K2×U2 – Fq2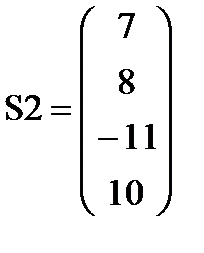

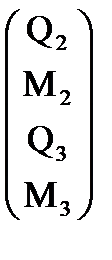
Конечный элемент № 3 (узлы с номерами 3 и 4)

Перемещения в узлах 3-го конечного элемента (м, рад):

U3:= C3×U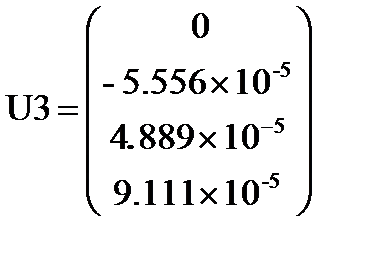

Внутренние усилия в узлах 3-го конечного элемента (кН, кН∙м):

S3:= K3× U3 – Fq3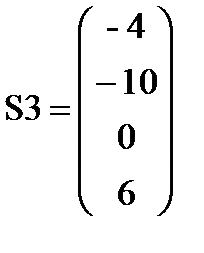

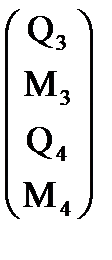
Эпюра внутренних изгибающих моментов :

 

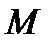Эпюра внутренних поперечных сил :

 

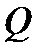6. Вычисление прогибов балки во внутренних сечениях конечных элементов с использованием функции формы

В результате расчёта балки методом конечных элементов получены значения прогибов u_i и углов поворота оси балки φ_i (первых производных от функции прогибов 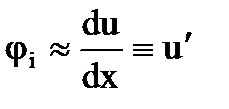) в узлах конечно-элементной сетки (тут i – номер узла, x – ордината вдоль оси балки). Для более точного построения эпюры прогибов по этим значениям u_i и φ_i можно проинтерполировать функцию прогибов u(x) внутрь каждого конечного элемента. Для такой интерполяции возможно использовать кубический полином, как частный случай полинома Эрмита:

P(x) = a + b∙x + c∙x² + d∙x³

 

Определим коэффициенты a, b, c, d кубического полинома P(x), интерполирующего внутри элемента функцию прогибов u(x), зная на концах элемента длиной l значения прогибов и углов поворота (первой производной от функции прогибов):

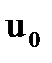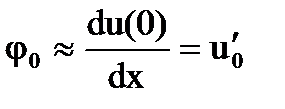, (при x = 0)

и 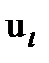, 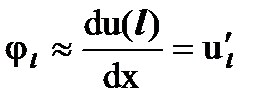(при x = l).

Ещё раз сформулируем эти 4 условия (как 4 уравнения относительно неизвестных коэффициентов a, b, c, d), которые полином P(x) должен исполнять на границах элемента:

при x = 0: P(0) = 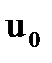и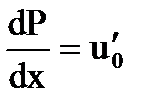

1) P(x = 0) = a, отсюда a = .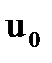

2) = b, отсюда b = .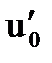

при x = l: P(0) = 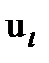и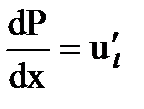

3) P(x = l) = a + b ∙ l + c ∙ l ² + d ∙ l ³ = .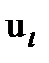

4) 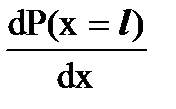= b + 2 ∙ c ∙ l + 3 ∙ d ∙ l ² = .

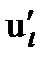Подставим очевидные из уравнений 1) и 2) значения коэффициентов a = 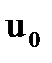и b = 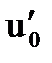в уравнения 3) и 4):

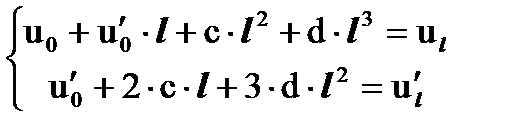
или относительно неизвестных c и d: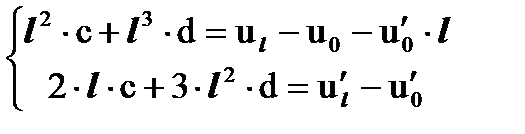

Решив эту систему из двух уравнений относительно неизвестных c и d, получаем:

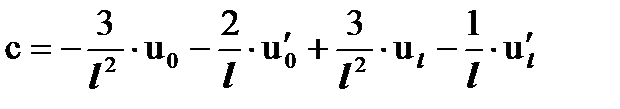
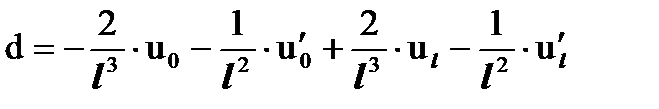
Подставим найденные значения коэффициентов a, b, c, d в полином P(x) = a + b∙x + c∙x² + d∙x³. Запишем 4 условия на границах конечного элемента уже с найденными выражениями для коэффициентов a, b, c, d. При этом сгруппируем слагаемые полинома P(x) при сомножителях , , , :

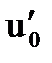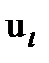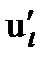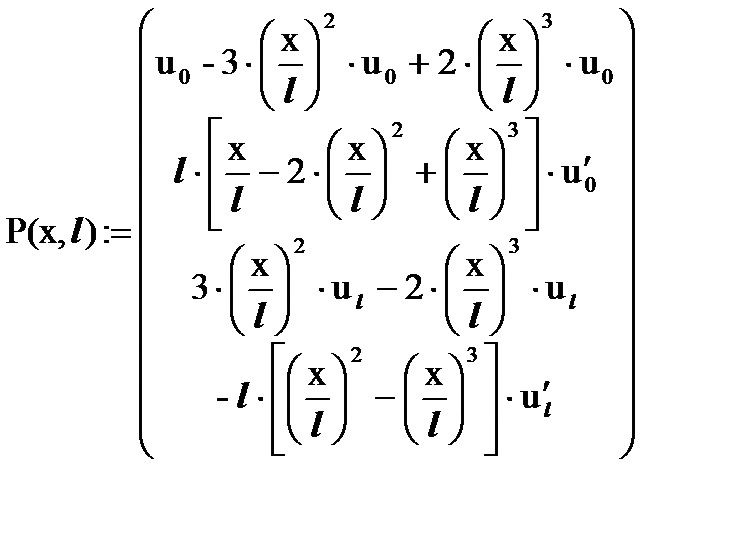
Теперь представим эту запись в виде скалярного произведения векторов:

,

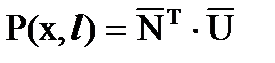где 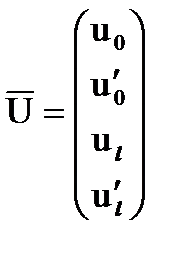, - вектор-функция формы конечного элемента.

Таким образом, полученный вектор функции формы N(x,L) балочного конечного элемента длиной L имеет общий вид:

Локальная ордината поперечного сечения элемента, в котором вычисляется прогиб

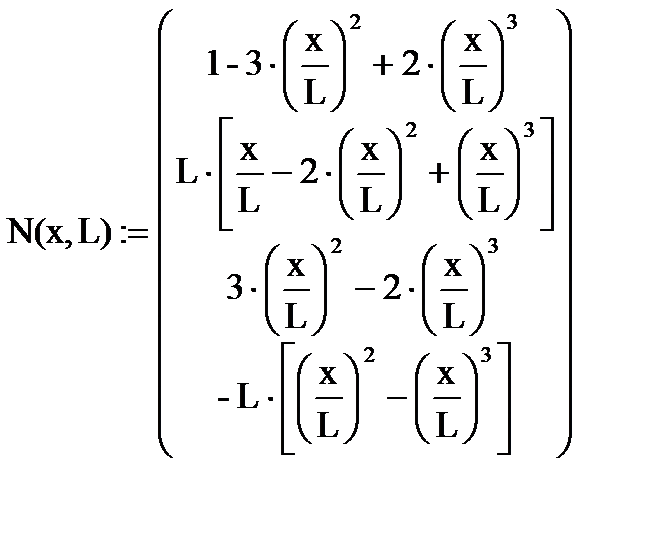
Вычисление прогибов в средней точке 1-го конечного элемента (x = 2.0м):

N(2.0, L1)^Т ∙U1 = 1.689 × 10 ^{– 4} (м)

Прогиб в середине 2-го элемента (x = 1.0м):

N(1.0, L2)^Т ∙U2 = 8.722 × 10 ^{– 5} (м)

Прогибы в серединных сечениях 3-го элемента (x = 0.5м и x = 1.0м):

N(0.5, L3)^Т ∙U3 = - 1.653 × 10 ^{– 5} (м)

N(1.0, L3)^Т ∙U3 = - 1.222 × 10 ^{– 5} (м)

Эпюра прогибов балки