Теорема о ранге.
Ранг матрицы соответствует количеству её линейно независимых строк, или столбцов.
Вопрос № 9: Вычисление ранга матрицы методом окаймляющих миноров:
Пусть в матрице найден минор порядка к, отличный от нуля, тогда достаточно рассмотреть лишь те миноры к+1 порядка, которые содержат внутри себя, то есть окаймляют минор к -ого порядка.
Если все они равны нулю, то минор к -ого порядка – базисный минор, а ранг матрицы равен рангу базисного минора, то есть матрица – к -ого порядка, ну а если существуют миноры, не равные нулю, ранг которых больше к, то операцию поиска необходимо продолжать. к:=л+1;
Пример:
М2 – базисный минор, ранг матрицы равен двум.
Вопрос № 10: Вычисление ранга матриц методом элементарных преобразований:
Элементарные преобразования матрицы:
1. Перестановка строк, или столбцов матрицы.
2. Умножение строки, или столбцы на число, отличное от нуля.
3. Сложение строк (столбцов) матрицы.
Теорема об элементарных преобразованиях матрицы:
При элементарных преобразованиях ранг матрицы не изменяется, поэтом при помощи элементарных преобразований матрица приводится к ступенчатому, или блочно треугольному виду, по которому ранг можно определить визуально.
Пример:
Правило определения ранга матрицы и её базисного минора:
1. Ранг ступенчатой матрицы равен количеству её не нулевых строк.
2. Базисный минор ступенчатой матрицы содержится среди элементов её не нулевых строк и такого же количества её столбцов, взятых по одному из каждой ступеньки.
Вопрос № 11: Теорема Кронекера-Капели:
1. Теорема Кронекера-Капели.
2. Общий метод решения систем из т алгебраических уравнений с п неизвестными.
Условие совместности
Рассмотрим произвольную систему из т уравнений с п неизвестными:
, тогда 
, 
Теорема Кронекера-Капели:
Система совместна, если ранг расширенной матрицы равен рангу матрицы коэффициентов.
Доказательство:
Необходимое условие:
Если система совместна, то ранг расширенной матрицы и ранг матрицы коэффициентов равны.
Следовательно, столбец свободных членов линейно зависит от столбцов матрицы коэффициентов, поэтом столбцы расширенной матрицы содержат тоже количество независимых столбцов, что и матрица коэффициентов, тогда добавление линейно зависимого столбца не изменит ранг матрицы. Следовательно, по теореме о ранге матрицы, ранг матрицы коэффициентов равен рангу расширенной матрицы.
Достаточное условие:
Применим правило Крамара к произвольной системе.
Пусть система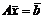 
совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
Назовём базисными те переменные, которые входят в базисный минор, а все остальные – свободными.
Тогда по теореме о базисном миноре нижние строки расширенной матрицы являются линейно зависимыми от первых строк, то есть могут быть представлены, как их линейные комбинации, следовательно, они являются лишними и могут быть отброшены. В результате остаётся система с r уравнениями и тем же количеством неизвестных, где r – ранг системы, или ранг базисного минора.
Перенесём свободные переменные направо, тогда получится система следующего вида:
, тогда у этой укороченной системы определитель 
. Число уравнений равно числу неизвестных, следовательно, к этой системе можно применить правило Крамара.
, 
, таким образом правило Крамара позволяет выразить базисные элементы через свободные. В результате придавая свободным переменным значения: 
, где С – произвольное действительное число. 
. Отсюда следует:
– множество решений системы уравнений содержит n-r произвольных постоянных, то есть является многопараметрическим.
Частный случай, когда ранг системы равен рангу матрицы коэффициентов, тогда все переменные являются базисными, значит свободных нет, а система имеет единственное решение.
Система линейных алгебраических уравнений имеет одно единственное решение, если она совместна, и её ранг равен количеству переменных.
Вопрос № 12: Метод Гаусса последовательного исключения неизвестных:
1. Метод Гаусса последовательного исключения неизвестных.
а) Матричная форма записи.
б) Прямой и обратный ход.
Метод последовательного исключения неизвестных заключается в решении системы алгебраических уравнений с одновременным исследованием её на совместность.
Метод реализуется в два этапа:
Прямой ход метода:
Прямой ход метода Гаусса заключается в преобразовании расширенной матрицы коэффициентов системы к ступенчатому виду с помощью элементарных преобразований, то есть как при нахождении ранга матрицы и базисного минора, но только со строками матрицы. При этом само преобразование к ступенчатому виду с помощью нескольких шагов, на каждом из которых исключается одна переменная, то есть обнуляется нижний элемент одного из столбцов.
В результате выполнения нескольких шагов матрица оказывается приведённой к ступенчатому виду. На этом этапе можно определить ранг матрицы и системы.