Лекция 1. Элементы комбинаторики

Цель: ознакомиться с основными понятиями комбинаторики и методами решения комбинаторных задач.

Комбинаторикой называется раздел математики, в котором решаются задачи на составление различных комбинаций из конечного числа элементов и подсчет всех возможных таких комбинаций.

Существует три основных вида задач в зависимости от постановки вопроса и того элемента комбинаторики, который применяется при их решении:

- задачи на перестановки;

- задачи на размещения;

- задачи на сочетания.

Перестановками из п элементов называются такие группы из п элементов, которые отличаются друг от друга лишь порядком следования элементов.

Число перестановок из п элементов обозначается символом Р_п.

Задача на перестановки формулируется так: пусть имеется п мест и п различных предметов. Спрашивается: сколькими способами эти п различных предметов можно разместить по п местам?

Возьмем какой-либо предмет из п различных предметов. Его можно разместить на п имеющихся мест п способами. Второй предмет при каждом из п положений первого предмета может быть помещен в п – 1 мест и, следовательно, два предмета могут быть размещены на п местах п (п – 1) различными способами. При каждом из п (п – 1) размещений третий предмет может быть помещен на п – 2 мест и, следовательно, три предмета на п местах могут быть размещены п (п – 1)(п – 2) способами и т. д.

Таким образом, п предметов могут быть размещены на п местах

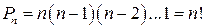
различными способами. Например, пусть имеется п одинаковых стульев, стоящих в ряд, и п различных людей, которые могут сидеть на этих стульях. Число п! дает число различных фотографий, которые можно получить, рассаживая различными способами этих людей по стульям. Например, три человека (мужчина, женщина, ребенок) можно рассадить на три стула 3! = 6 способами:

Размещениями из п элементов по т называются такие группы из m элементов, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их следования.

Число размещений из п элементов по т обозначается символом .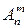

Задача на размещения формулируется так: пусть имеется т различных предметов. Спрашивается: сколькими способами их можно разместить по п местам? При каждом размещении т предметов п – т мест будут свободными. Если бы эти п – т мест были заняты различными предметами, то при каждом фиксированном расположении т предметов их можно было бы разместить (п – т)! различными способами. Если перебрать все возможные размещения т предметов по п местам и при каждом из них произвести (п – т)! размещений п – т других предметов на оставшихся п – т местах, то всего получается число различных размещений т + (п – т) = п различных предметов по п различным местам, т. е. п! Следовательно, искомое число способов размещения т предметов по п различным местам

.

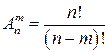Необходимо себе представить, что при этом понимается под различными способами размещения. Возвращаясь к примеру с фотографиями, мы под т должны понимать число различных людей, а под п – число стульев, на которых они могут сидеть. Тогда 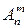означает число различных фотографий, причем различными считаются не только те фотографии, на которых, например, неодинакова последовательность, в которой сидят люди, но и те, на которых они сидят в той же последовательности, но на других стульях. Поэтому две фотографии, на которых они сидят рядом друг с другом в определенной последовательности слева направо и занимают стулья с 1-го по т -й (стулья стоят в один ряд), отличны от фотографии, где они сидят точно так же, но занимают стулья со 2-го по ( т + 1)-й. Например, на трех стульях (п = 3) два человека (мужчина и женщина) могут быть рассажены 3!/[(3 – 2)!] =6 способами:

Сочетаниями из п элементов по т называются такие группы из m элементов, которые отличаются друг от друга хотя бы одним элементом.

Число сочетаний из п элементов по т обозначается символом .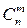

Задача на сочетания формулируется так: пусть имеется п различных предметов. Спрашивается: сколькими способами можно выбрать из них группу из т предметов, чтобы все группы были разными (отличаются составом предметов)? Порядок предметов в группе не играет роли. Эту задачу можно решить следующим образом. Если в группу входит один предмет, то из п предметов можно образовать п различных групп. Различные группы из двух предметов образуются так: каждый из различных п предметов комбинируется оставшимися п – 1 предметами, т. е. общее число комбинаций п (п – 1).

Однако комбинации, отличающиеся лишь порядком, считаются одинаковыми. Число перестановок для двух предметов равно 2!, и, следовательно, общее число различных групп по два предмета, которые можно образовать из п предметов, равно п(п – 1)/2! Продолжая эти рассуждения, приходим к выводу, что число способов, которыми можно выбрать т различных предметов из п различных предметов,

.

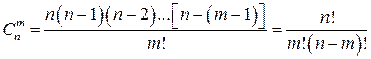Пусть имеется группа из трех человек (п = 3) – мужчина, женщина, ребенок, образующие группу «предметов», из которой производится выборка подгруппы.

Ясно, что группа «предметов» полностью удовлетворяет условиям применимости последней формулы: как в полной группе, так и в выборках по подгруппам порядок следования «предметов» или их взаимное расположение не имеет значения. Из них можно сформировать группы по т = 2 человека. Число различных групп равно 3! / [2! (3 – 2)!] = 3:

Отметим, что выше предполагалось, что все полученные группы предметов состоят из различных элементов. Такие группы называются группами без повторений. Группы с повторениями, для вычисления количества которых используются совсем другие формулы, мы здесь не рассматриваем.

Из всего разнообразия математических задач задачи по комбинаторике легко узнаются по формулировке поставленного вопроса: «Сколькими способами?», «Сколько вариантов?» и т.д.

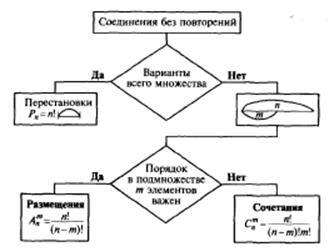
При решении комбинаторных задач (без повторений) удобно использовать алгоритм (см. рис.), в котором требуется найти ответы на два «ключевых» вопроса:

• во всем ли множестве необходимо найти число возможных вариантов?

• важен ли порядок расположения отдельных элементов в ис­следуемом множестве (подмножестве)?

Пример 1.Восемь студентов обменялись рукопожатиями. Сколь­ко было рукопожатий?

Решение. В рукопожатии участвует «подмножество», состоящее из двух студентов (m = 2), тогда как все «множество» студентов составляет 8 человек (n = 8). Так как в процессе рукопожатия порядок не важен, выбираем формулу сочетаний

.

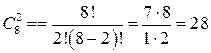Пример 2. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезов материи?

Решение. Порядок важен, так как перестановка материи внутри трехцветного флага обозначает разные страны. Поэтому выбираем формулу размещений без повторений, где множество отрезов материи содержит п= 5. а подмножество – т = 3 цветов:

.

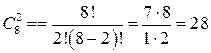Пример 3.Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

Решение. Множество включает n = 6 языков. Поскольку перевод есть отношение между двумя языками, то m = 2, причем порядок важен, так как, например, словари англо-русский и русско-английский имеют различное применение. Поэтому выбираем размещения без повторений:

Пример 4. Сколько имеется вариантов составления расписания на понедельник, если предметов у студентов 9, а в понедельник четыре пары занятий и предметы не повторяются?

Решение, а) Для студентов порядок не важен, поэтому выбираем сочетания без повторений: .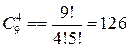

б) Для преподавателей порядок важен, поэтому выбираем формулу размещений без повторений: .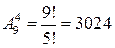

Пример 5. Сколькими способами можно расставить на книжной полке девять книг, среди которых есть трехтомник А. С. Пушкина?

Решение. Так как три тома, входящие в трехтомник, должны стоять рядом, причем по возрастанию номера тома слева направо, рассматриваем их как один элемент данного множества, в котором имеется еще шесть элементов. Поэтому выбираем перестановки без повторений во множестве, содержащем семь элементов:

.

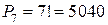Пример 6. Сколькими способами можно назначить в группе из 30 человек трех дежурных?

Решение. а) Если их роль в процессе дежурства одинакова, то порядок не важен, поэтому выбираем сочетания без повторений:

.

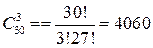б) Если порядок важен, т. е. во время дежурства их функциональные обязанности различны, то по формуле размещений без повторений имеем: .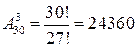

Вопросы для самоконтроля:

1. Что изучает комбинаторика?

2. Перечислите основные виды задач комбинаторики.

3. Что называют перестановками? Как найти число перестановок из п элементов?

4. Что называют размещениями? Как найти число размещений т предметов по п местам?

5. Что называют сочетаниями? Как найти число сочетаний из п элементов по т?