Задание 1
Только 94% из 27 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
Решение.
Правильно решили задачу 27 500 · 0,94 = 25 850 учеников.
Ответ: 25 850.
Задание 2
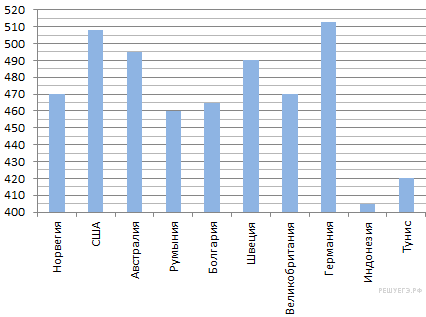
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по математике в 2007 году (по 1000-балльной шкале). Найдите средний балл участников из Болгарии.
Решение.
Средний балл участников из Болгарии указывает пятый столбец диаграммы. Он равен 465.
Ответ: 465.
Задание 3
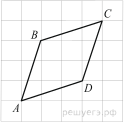
На клетчатой бумаге с размером клетки 
изображён четырёхугольник ABCD. Найдите его периметр.
Решение.
Стороны четырехугольника равны. По теореме Пифагора,
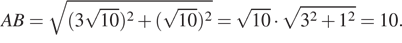
Следовательно, периметр равен 
Ответ: 40.
Задание 4
Вероятность того, что на тестировании по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Решение.
Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
Ответ: 0,07.
Задание 5
Найдите решение уравнения: 
Решение.
Перейдем к одному основанию степени:
Ответ: 4.
Задание 6
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение.
Выразим площадь двумя способами:
Тогда, 
Ответ: 6.
Задание 7
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Решение.
Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции неотрицательна, то есть промежуткам (−11; −10], [−7; −1], [2; 3). Наибольший из них — отрезок [−7; −1], длина которого 6.
Ответ: 6.
Задание 8
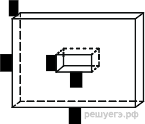Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:
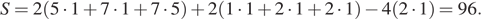
Ответ: 96.
Задание 9
Найдите значение выражения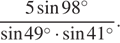 
Решение.
Выполним преобразования:
Ответ: 10.
Задание 10
Для обогрева помещения, температура в котором поддерживается на уровне 
, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу воды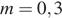 
кг/с. Проходя по трубе расстояние 
, вода охлаждается от начальной температуры 
до температуры 
, причeм 
, где 
— теплоeмкость воды, 
— коэффициент теплообмена, а 
— постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.
Решение.
Задача сводится к решению уравнения 
при заданных значениях теплоёмкости воды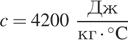 
, коэффициента теплообмена 
, постоянной 
, температуры помещения и расхода воды 
:
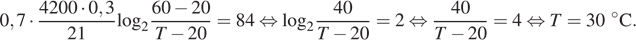
Ответ: 30.
Задание 11
Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Решение.
Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 
км — весь путь путешественника, тогда средняя скорость равна:
Поэтому средняя скорость путешественника 38,4 км/ч.
Ответ: 38,4.
Задание 12
Найдите точку минимума функции 
Решение.
Найдем производную заданной функции:
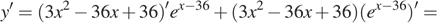
Найдем нули производной:
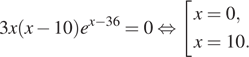
Определим знаки производной функции и изобразим на рисунке поведение функции:
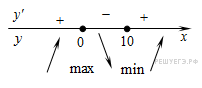
Искомая точка минимума 
Ответ: 10.
Задание 13
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку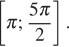 
Решение.
а) Преобразуем уравнение:
Следовательно,
где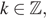 
откуда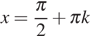 
б) 
С помощью числовой окружности отберём корни, принадлежащие отрезку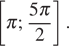 
Получим числа 
Ответ: а) 
где 
б) 
Задание 14
Точки 
и 
— середины рёбер 
и 
куба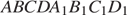 
соответственно.
а) Докажите, что прямые 
и 
перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку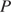 
и перпендикулярной прямой 
, если ребро куба равно 10.
Решение.
а) Проведём отрезок 
, параллельный 
Пусть 
— точка пересечения отрезков 
и 
Треугольник 
прямоугольный с прямым углом при вершине 
Это следует из равенства треугольников 
и 
Значит, прямые и перпендикулярны. Прямые и 
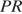перпендикулярны, так как прямая 
перпендикулярна плоскости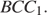 
Поэтому прямая перпендикулярна плоскости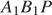 
, и, следовательно, прямая перпендикулярна прямой 
б) Указанное сечение — прямоугольник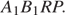 
Его площадь равна 
Ответ: б)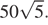 
Задание 15
Решите неравенство: 
Решение.
Решим неравенство методом интервалов:
Ответ: 
Задание 16 № 507889
Хорды AD, BE и CF окружности делят друг друга на три равные части.
а) Докажите, что эти хорды равны.
б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E последовательно расположены на окружности, а радиус окружности равен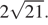 
Решение.
а) Пусть две хорды равны 3 x и 3 y. По теореме о произведении пересекающихся хорд 2 x · x = 2 y · y. Отсюда находим, что x = y, значит, эти хорды равны. Аналогично докажем, что третья хорда равна каждой из первых двух.
б) Равные хорды равноудалены от центра окружности, поэтому центр равностороннего треугольника с вершинами в точках попарного пересечения хорд совпадает с центром данной окружности. Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.
Через точку T проведём прямую, параллельную AD, через точку P — прямую, параллельную CF, а через точку Q — прямую, параллельную BE. Эти прямые и хорды AD, BE и CF разбивают шестиугольник ABCDEF на 13 одинаковых равносторонних треугольников.
Обозначим PQ = 2 a. Тогда
Отсюда находим, что a = 3, значит, PQ = 2 a = 6, 
Следовательно,
Ответ: 
Задание 17
Садовод привез на рынок 91 кг яблок, которые после транспортировки разделил на три сорта. Яблоки первого сорта он продавал по 40 руб., второго сорта – по 30 руб., третьего сорта – по 20 руб. за килограмм. Выручка от продажи всех яблок составила 2170 руб. Известно, что масса яблок 2-го сорта меньше массы яблок 3-го сорта на столько же процентов, на сколько процентов масса яблок 1-го сорта меньше массы яблок 2-го сорта. Сколько килограммов яблок второго сорта продал садовод?
Решение.
Пусть x кг — масса яблок 1-го сорта, y кг — масса яблок 2-го сорта, оставшиеся 91 − (x + у) кг — масса яблок 3-го сорта. Для величины выручки имеем:
откуда 
(*).
Поскольку масса яблок 1-го сорта меньше массы яблок 2-го сорта на столько же процентов, на сколько процентов масса яблок 2-го сорта меньше массы яблок 3-го сорта имеем:
Подставим условие (*) в полученную пропорцию и решим ее:
Тем самым, садовод продал 7 кг яблок первого сорта и, следовательно, 35 − 14 = 21 кг яблок второго сорта.
Ответ: 21.
Приведём другое решение.
Пусть x кг — масса яблок первого сорта, проданных садоводом, а масса яблок второго сорта составляет tx кг. Тогда масса проданных яблок третьего сорта составит tx · t = t 2 x кг. По условию задачи:
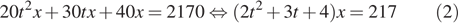
Поделив почленно равенство (2) на равенство (1), получим:
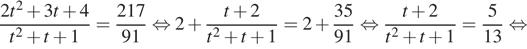
Значение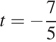 
не подходит по смыслу задачи. Значение x найдем из уравнения 
Ответ: 21 кг.
Задание 18
Найдите все значения а, при каждом из которых система уравнений
имеет ровно четыре различных решения.
Решение.
Второе уравнение приводится к виду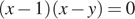 
, откуда 
При a = 0 исходная система имеет одно решение.
При 
при подстановке в первое уравнение системы 
получаются квадратные уравнения. Значит, исходная система уравнений имеет ровно 4 различных решения тогда и только тогда, когда каждое из этих уравнений имеет ровно два корня и пара чисел (1;1) не является решением исходной системы.
При x = 1 получаем:
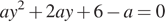
Это квадратное уравнение имеет ровно два корня при положительном дискриминанте:
откуда a < 0 и a > 3.
При 
получаем:
Это квадратное уравнение имеет два корня при положительном дискриминанте:
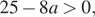
откуда, учитывая условие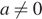 
, получаем 
и 
.
Пара чисел (1;1) является решением исходной системы при 
то есть a = −3.
Таким образом, исходная система уравнений имеет ровно 4 решения при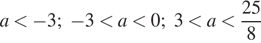 
.
Ответ: 
.
Задание 19
В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам некоторого отдела на общую сумму 600 000 рублей (размер премии каждого сотрудника — целое число, кратное 1000). Бухгалтеру дают распределение премий, и он должен их выдать без сдачи и размена, имея 100 купюр по 1000 рублей и 100 купюр по 5000 рублей.
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, если ведущему специалисту надо выдать 40 000 рублей, а остальные поделить поровну на 70 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
Решение.
а) Разделим общую сумму в 600 000 руб. на 40, получим, что каждый должен получить по 15 000 руб. Так как это число кратно и 1000 и 5000, то всем 40 сотрудникам можно раздать равную премию в указанных купюрах.
б) Сумма, оставшаяся после выплаты 40 000 руб., будет равна 560 000 руб. При делении на 70 сотрудников получаем выплаты по 8000 руб. Так сделать не удастся, поскольку 8000 = 5000 + 3 · 1000 и для 70 сотрудников нужно будет 210 тысячных купюр, а их всего 100.
в) Если сотрудников 27 или больше, то распределим премии так: 26 человека должны получить по 4 тысячи, один — всё остальное. Тогда выдать премии будет нельзя по тем же причинам, что и в пункте «б».
Если же их не больше 26, то выберем всех, кроме одного. Будем выдавать им премии, используя не более четырёх тысячных купюр, пока не кончится пятитысячные.
Если пятитысячные купюры закончились, то оставшиеся премии выдать точно удастся. Если же нет, то все премии, кроме одной, будут выданы, а последний просто заберёт все оставшиеся деньги.
Ответ: а) да; б) нет; в) 26.