Уважаемые студенты, вам предложены новые задания по математике по теме «Треугольник Паскаля».
Прочитайте статью «Удивительный треугольник великого француза» и напишите (по желанию) небольшое эссе (объем до 1 страницы) о том, кого вы считаете самым значительным ученым за прошедшие 2000 лет. За задание выставляется оценка! Рекомендую присылать выполненные работы на электронную почту katja.pavlova@mail.ru или в сообщениях ВКОНТАКТЕ до конца недели. Удачи!
Удивительный треугольник великого француза
(Опубликовано в журнале Hard'n'Soft №10 2003)
На сайте журнала "Знание-сила" есть голосование по вопросу о том, кого вы считаете самым значительным ученым за прошедшие 2000 лет. И, естественно, среди самых популярных ученых мы по праву видим имя Блеза Паскаля (1623-1662).
Паскаль умер, когда ему было 39 лет, но, несмотря на столь короткую жизнь, он вошел в историю как выдающийся математик, физик, философ и писатель. Его именем благодарными потомками названы единица давления (паскаль) и получивший чрезвычайно широкое распространение язык программирования. Особенно популярен был Турбо Паскаль 5.5 для ДОС, ныне - Борланд Паскаль 7.0 и его дальнейшее развитие в Delphi. Работы Паскаля охватывают самые разные области. Он является одним из создателей математического анализа, проективной геометрии, теории вероятностей, гидростатики (широко известен закон Паскаля, в соответствии с которым изменение давления в покоящейся жидкости передается в остальные ее точки без изменений), создателем механического счетного устройства - "паскалева колеса" - как говорили современники. Паскаль продемонстрировал, что воздух обладает упругостью, и доказал, что он имеет вес, открыл, что показания барометра зависят от влажности и температуры воздуха и потому его можно использовать для предсказания погоды.
Некоторые из практических достижений Паскаля удостоились высшего отличия - сегодня мало кто знает имя их автора. Например, сейчас очень немногие скажут, что самая обыкновенная тачка - это изобретение Блеза Паскаля. Ему же принадлежит идея омнибусов - многоместных конных экипажей с фиксированными маршрутами - первого вида регулярного общедоступного городского транспорта. Уже в шестнадцатилетнем возрасте Паскаль сформулировал теорему о шестиугольнике, вписанном в коническое сечение (теорема Паскаля). (Известно, что позже он получил из своей теоремы около 400 следствий.) Через несколько лет Блез Паскаль создал механическое вычислительное устройство - суммирующую машину, которая позволяла складывать числа в десятичной системе счисления. В этой машине цифры задавались путем соответствующих поворотов дисков (колесиков) с цифровыми делениями, а результат операции можно было прочитать в окошках - по одному на каждую цифру.
Блез Паскаль и другой великий француз, Пьер Ферма, стали основателями теории вероятностей, причем годом ее рождения часто называют 1654-й, когда Паскаль и Ферма независимо друг от друга дали правильное объяснение так называемого парадокса раздела ставки. Два игрока играют в "безобидную" игру (т.е. шансы победить у обоих одинаковы), договорившись, что тот, кто первым выигрывает шесть партий, получит весь приз. Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл пять партий, а второй - три). Как справедливо разделить приз? Хотя, вообще говоря, данная проблема не является парадоксом, безуспешные попытки некоторых видных ученых ее решить, а также неверные ответы создали легенду о парадоксе. Так, согласно одному решению следовало разделить приз в отношении 5: 3, т.е. пропорционально выигранным партиям, согласно другому - в отношении 2: 1 (здесь рассуждения велись, по всей видимости, следующим образом: поскольку первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы шести партий, то он должен получить одну треть от приза, а оставшуюся часть нужно разделить пополам).
А между тем делить надо в отношении 7:1. И Паскаль, и Ферма рассматривали парадокс раздела ставки как задачу о вероятностях, установив, что справедливым является раздел, пропорциональный шансам первого игрока выиграть приз. Предположим, первому игроку осталось выиграть только одну партию, а второму для победы необходимо выиграть еще три партии, причем игроки продолжают игру и играют все три партии, даже если некоторые из них окажутся лишними для определения победителя. Для такого продолжения все 23 = 8 возможных исходов будут равновероятными. Так как второй игрок получает приз только при одном исходе (если он выиграл все три партии), а в остальных случаях побеждает первый игрок, справедливым является отношение 7: 1. (Паскаль и Ферма нашли также общее решение для случая, когда одному игроку для получения приза нужно выиграть еще n партий, а другому - m партий.)
Но, наверное, самой известной математической работой Блеза Паскаля является трактат об "арифметическом треугольнике", образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами. Рассмотрением этого волшебного треугольника мы и займемся.
В действительности, треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Мартин Гарднер пишет в книге "Математические новеллы" (М., Мир, 1974): "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".
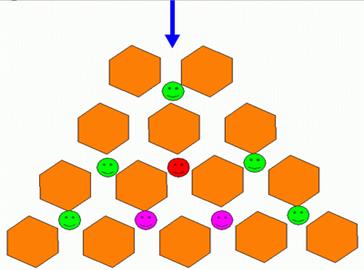Предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смаликом, а тремя, соответственно, розовым. Это один из вариантов построения треугольника, предложенный Гуго Штейнгаузом в его классическом "Математическом калейдоскопе".
А еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.
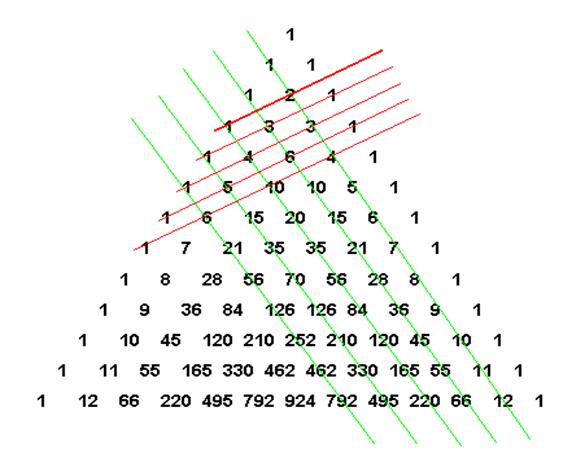
На вершине треугольника стоит 1. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей.
Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа - один шар мы можем положить на три - итого четыре, под три подложим шесть (напрягитесь и представьте!) - итого десять, и так далее. Подробнее о треугольных числах можно прочитать в Hard'n'Soft №4 2002 в статье "Кролики-каннибалы, четверостишия и заповедник последовательностей" доступной также на Арбузе.
А следующая зеленая линия (1, 5, 15, 35,...) продемонстрирует попытку выкладывания гипертетраэдра в четырехмерном пространстве - один шар касается четырех, а те, в свою очередь, десяти... В нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов.
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда? Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.
Даже беглого взгляда, брошенного на треугольник Паскаля, достаточно, чтобы отметить следующие любопытные факты: 10 ядер можно сложить и в виде тетраэдра и в виде плоского треугольника. А 56 гиперядер, образующих тетраэдр в пятимерном пространстве, можно уложить в обычный привычный трехмерный тетраэдр, однако, если бы мы попытались выложить из 56 ядер треугольник, то одно ядро осталось бы лишним.
Как же нам нарисовать треугольник Паскаля чтобы поиграть с ним? Лучше всего использовать идею, рассмотренную нами при программировании шестиугольной жизни в Hard'n'Soft №5 2002 (на Арбузе), а именно - берется обычный двумерный массив, но при выводе на экран ряды через один сдвигаются - четные ряды вправо на четверть шага, нечетные влево на четверть шага, и тогда ряды смещены на полшага, что дает нам шестиугольную структуру поля при прямоугольном массиве. А двумерность массива позволяет очень легко с ним работать, задав в цикле по строкам и рядам действия над ячейкой.
Теперь, наконец-то, переходим к самому интересному для нас удивительному свойству треугольника Паскаля. Заменим каждое число в треугольнике Паскаля точкой. Причем, нечетные точки выведем контрастным цветом, а четные - прозрачным, или цветом фона. Результат окажется непредсказуемо-удивительным: треугольник Паскаля разобьется на более мелкие треугольники, образующие изящный узор. Узоры эти таят в себе много неожиданностей. По мере удаления от вершины нам будут встречаться треугольники все возрастающих размеров, не содержащие ни одной жирной точки, то есть "составленные" из одних лишь четных чисел. У вершины треугольника Паскаля "притаился" треугольник состоящий из одной - единственной точки, затем идут треугольники, содержащие 6, 28, 120, 496,... точек. Три из названных чисел - 6, 28 и 496 - известны как совершенные, поскольку каждая из них равно сумме всех своих делителей, отличных от самого числа. Например, 6=1+2+3. Неизвестно, существует ли бесконечно много совершенных чисел, а также существует ли хоть одно нечетное совершенное число. Подробнее о совершенных числах можно прочитать на 
Арбузе.
Приведем программу, реализующую расцветку треугольника в соответствии с четностью каждого числа треугольника. Вместо значения числа на его месте рисуется круг, заливаемый черным цветом для нечетных значений и белым для четных.
Любителям математики сразу же бросится в глаза "фрактальность" полученного объекта, а точнее, мы видим не что иное, как "Треугольник Серпинского", аналог знаменитого "Ковра Серпинского".
Движемся далее - пробуем проверять не четность, а остаток от деления на другие числа, и каждый раз удивляемся открывающимся видом треугольника. Поиграв некоторое время, заметим, что при задании числа, деление на которое мы проверяем, простым, получаются красивые орнаменты с ярко выраженной закономерностью, а при делении на составное число орнамент рассыпается, сохраняя, впрочем, симметрию и закономерность в чередовании узоров. Причем, чем больше делителей имеет проверяемое число (например, 12 делится на 2, на 3, 4 и 6), тем более "размытым" получается узор.
Рассмотрите треугольник, построенный "относительно" числа 7, то есть, числа, не делящиеся на 7 без остатка, нарисованы черным цветом, делящиеся - белым, и попробуйте увидеть закономерности.
Попробуем раскрасить треугольник Паскаля. Для этого назначим три переменных (r,g,b), ответственных, соответственно, за красную, зеленую и синюю составляющую раскраски ячейки и привяжем их значение (максимальное может быть равным 255) к проверке делимости на разные числа.
И вот результат работы программы. Не правда ли красиво? Видны красные треугольные "зоны Серпинского", которые, накладываясь на зеленые окошки от девяток, дают желтые зоны, а с синими участками от деления на 11 дают сиреневые участки. Имеет ли эта красота прикладное значение кроме узора для обоев пока не ясно, но от треугольника Паскаля, особенно цветного, можно ожидать любых чудес, возможно, и в скором будущем.
А вот еще один вариант раскраски, выполненный по алгоритму