| §1 Комбинаторика | ||||||||||
Рассмотрим множество, состоящее из 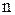 различных элементов. Число множеств, состоящих из k элементов,
отбираемых из множества, содержащего n элементов различных элементов. Число множеств, состоящих из k элементов,
отбираемых из множества, содержащего n элементов
Требуется выбрать из них какие-нибудь Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество
Любое подмножество (неупорядоченное), состоящее из Число сочетаний без повторений Число сочетаний с повторениями
Количество способов переставить
| Задача.
В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?
Решение.
Задача на число размещений, т.к. флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать 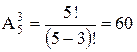 штук.
Задача.
Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.
Решение.
По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов - штук.
Задача.
Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.
Решение.
По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов - 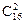 . Так как команды должны играть дважды число вариантов удваивается, т.е. . Так как команды должны играть дважды число вариантов удваивается, т.е.  .
Задача.
Количество перестановок букв в слове «цифра » равно…
Варианты ответов: 1) 25 2) 20 3) 120 4) 5
Решение.
Количество перестановок для n различных элементов (в данном случае - различных букв) равно n!. Таким образом, для слова «цифра » количество перестановок равно 5!=120.
Ответ. №3.
Задача.
Сколько различных перестановок можно составить из букв слова «задача»?
Решение.
Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть .
Задача.
Количество перестановок букв в слове «цифра » равно…
Варианты ответов: 1) 25 2) 20 3) 120 4) 5
Решение.
Количество перестановок для n различных элементов (в данном случае - различных букв) равно n!. Таким образом, для слова «цифра » количество перестановок равно 5!=120.
Ответ. №3.
Задача.
Сколько различных перестановок можно составить из букв слова «задача»?
Решение.
Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть  . .
| |||||||||
| §2 Вычисление вероятности по классической формуле | ||||||||||
Вероятность события 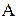 определяется формулой определяется формулой
 ,
где ,
где  число элементарных исходов, благоприятствующих событию число элементарных исходов, благоприятствующих событию 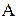 ; ;
 число всех возможных элементарных исходов испытания.
Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. число всех возможных элементарных исходов испытания.
Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
| Задача.
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более трех очков, равна…
Варианты ответов: 1)  2) 2) 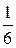 3) 3)  4) 4)  Решение.
Игральная кость содержит 6 граней, т.о. при ее бросании возможно 6 равновероятных исходов. Событие " выпадет не более трех очков " равносильно выпадению 1, 2 или 3 очков. Тогда по формуле классической вероятности получаем
Решение.
Игральная кость содержит 6 граней, т.о. при ее бросании возможно 6 равновероятных исходов. Событие " выпадет не более трех очков " равносильно выпадению 1, 2 или 3 очков. Тогда по формуле классической вероятности получаем
 .
Ответ. №4. .
Ответ. №4.
| |||||||||
| §3 Геометрическое и статистическое определения вероятности | ||||||||||
Если опыт сводится к бесконечному числу равновозможных случаев, то применяется геометрическое определение вероятности
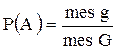 ,
где ,
где 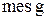 равно длине отрезка, если точки множества равно длине отрезка, если точки множества  расположены на прямой; расположены на прямой; 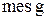 равно площади фигуры, если точки множества равно площади фигуры, если точки множества  расположены на плоскости; расположены на плоскости; 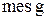 равно объему тела, если точки множества равно объему тела, если точки множества  расположены в пространстве. расположены в пространстве.
| Задача.
Территория нефтебазы имеет форму прямоугольника со сторонами  м, м, 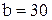 м. На территории имеется емкость диаметром 10 м. (см.рис.). Какова вероятность поражения емкости бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку равновероятное?
Решение.
Событие А - поражение емкости бомбой, попавшей на территорию нефтебазы м. На территории имеется емкость диаметром 10 м. (см.рис.). Какова вероятность поражения емкости бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку равновероятное?
Решение.
Событие А - поражение емкости бомбой, попавшей на территорию нефтебазы  , где , где 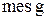 площадь заштрихованного круга; площадь заштрихованного круга; 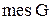 - площадь прямоугольника - площадь прямоугольника
  . .
| |||||||||
| §4 Теоремы сложения и умножения вероятностей | ||||||||||
Суммой двух событий  и и  называется событие называется событие  , состоящее в появлении или события , состоящее в появлении или события  , или события , или события  , или обоих вместе. Ключевое слово «или» («либо»).
Произведением двух событий , или обоих вместе. Ключевое слово «или» («либо»).
Произведением двух событий  и и  называется событие называется событие  , состоящее в совместном выполнении события , состоящее в совместном выполнении события  и события и события  . Ключевое слово «и».
Два события называются несовместными, если они не могут появиться одновременно.
Теорема сложения. . Ключевое слово «и».
Два события называются несовместными, если они не могут появиться одновременно.
Теорема сложения.
 для несовместных событий; для несовместных событий;
 для совместных событий.
Два события называются независимыми,если вероятность одного из них не зависит от появления или непоявления другого.
Условной вероятностью для совместных событий.
Два события называются независимыми,если вероятность одного из них не зависит от появления или непоявления другого.
Условной вероятностью  называют вероятность события называют вероятность события  , вычисленную в предположении, что событие , вычисленную в предположении, что событие 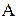 уже наступило.
Теорема умножения. уже наступило.
Теорема умножения.
 для независимых событий; для независимых событий;
 для зависимых событий. для зависимых событий.
| Задача.
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,2 и 0,35. Тогда вероятность банкротства обоих предприятий равна…
Варианты ответов: 1) 0,07 2) 0,55 3) 0,7 4) 0,52
Решение.
Рассмотрим события А -"банкротство I предприятия" и B -"банкротство II предприятия". По условию эти события независимы, тогда по теореме о произведении независимых событий получаем 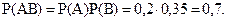 Ответ. №3.
Задача.
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
Варианты ответов: 1) 0,45 2) 0,5 3) 0,36 4) 0,4
Решение.
Рассмотрим события А -"в цель попал I стрелок" и B -" в цель попал II стрелок ". По условию эти события независимы, тогда по теореме о произведении независимых событий получаем
Ответ. №3.
Задача.
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
Варианты ответов: 1) 0,45 2) 0,5 3) 0,36 4) 0,4
Решение.
Рассмотрим события А -"в цель попал I стрелок" и B -" в цель попал II стрелок ". По условию эти события независимы, тогда по теореме о произведении независимых событий получаем  Ответ. №3.
Задача.
Случайные события А и В - несовместны. Тогда выполнено …
Варианты ответов: 1) p(A)+p(B)=1 2) p(A)+p(B)£1
3) p(A+B)<1 4) p(AB)=1
Решение.
Разберем варианты ответов
1) p(A)+p(B)=1 - события А и В - несовместны и противоположны
2) p(A)+p(B)£1 - события А и В - несовместны
3) p(A+B)<1 - события А и В могут быть совместны, могут быть несовместны
4) p(AB)=1 - события А и В - совместны
Ответ. №2.
Ответ. №3.
Задача.
Случайные события А и В - несовместны. Тогда выполнено …
Варианты ответов: 1) p(A)+p(B)=1 2) p(A)+p(B)£1
3) p(A+B)<1 4) p(AB)=1
Решение.
Разберем варианты ответов
1) p(A)+p(B)=1 - события А и В - несовместны и противоположны
2) p(A)+p(B)£1 - события А и В - несовместны
3) p(A+B)<1 - события А и В могут быть совместны, могут быть несовместны
4) p(AB)=1 - события А и В - совместны
Ответ. №2.
| |||||||||
| §5 Формула полной вероятности. Формула Бейеса | ||||||||||
Допустим, что предполагается провести опыт, об условиях которого можно сделать 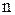 исключающих друг друга предположений (гипотез) исключающих друг друга предположений (гипотез)  , причем , причем  .
Вероятность некоторого события А, которое может появиться только вместе с одной из гипотез, вычисляется по формуле .
Вероятность некоторого события А, которое может появиться только вместе с одной из гипотез, вычисляется по формуле
 Эта формула носит название формулы полной вероятности.
Если же событие А совершилось и необходимо найти вероятность того, что оно произошло совместно с некоторой гипотезой
Эта формула носит название формулы полной вероятности.
Если же событие А совершилось и необходимо найти вероятность того, что оно произошло совместно с некоторой гипотезой 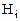 , то необходимо воспользоваться формулой Бейеса , то необходимо воспользоваться формулой Бейеса
 . .
| Задача.
Событие А может наступить лишь при условии появления одного из двух несовместных событий  и и 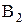 , образующих полную группу событий. Известны вероятность , образующих полную группу событий. Известны вероятность 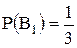 и условные вероятности и условные вероятности 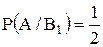 , , 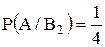 . Тогда вероятность . Тогда вероятность 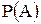 равна …
Варианты ответов: 1) равна …
Варианты ответов: 1)  2) 2)  3) 3) 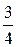 4) 4)  Решение.
Т.к. по условию несовместные события
Решение.
Т.к. по условию несовместные события  и и 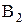 , образуют полную группу событий и известно, что вероятность , образуют полную группу событий и известно, что вероятность 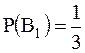 , то вероятность , то вероятность 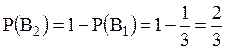 . Тогда по формуле полной вероятности получаем . Тогда по формуле полной вероятности получаем
 Ответ. №4.
Ответ. №4.
| |||||||||
| §6 Повторные испытания | ||||||||||
Пусть проводится 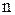 испытаний, причем выполняются следующие условия:
испытания независимы, то есть начальные условия перед каждым испытанием абсолютно одинаковы;
в каждом испытании интересующее нас событие А может произойти с вероятностью испытаний, причем выполняются следующие условия:
испытания независимы, то есть начальные условия перед каждым испытанием абсолютно одинаковы;
в каждом испытании интересующее нас событие А может произойти с вероятностью  .
Тогда вероятность того, что в .
Тогда вероятность того, что в 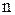 испытаниях событие наступит ровно испытаниях событие наступит ровно 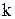 раз (безразлично, в какой последовательности), вычисляется по формуле Бернулли раз (безразлично, в какой последовательности), вычисляется по формуле Бернулли
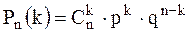 , где , где 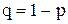 В случае, если
В случае, если 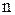 велико, то есть велико, то есть 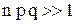 (значительно больше 1), то данную вероятность можно найти по асимптотической формуле (локальная теорема Лапласа): (значительно больше 1), то данную вероятность можно найти по асимптотической формуле (локальная теорема Лапласа):
 , где , где  .
Функция .
Функция  определяется формулой определяется формулой  .
Таблица значений функции .
Таблица значений функции 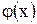 для положительных значений для положительных значений  приведена в приложении 1; для отрицательных значений приведена в приложении 1; для отрицательных значений  надо помнить, что надо помнить, что  .
В тех случаях, когда число испытаний .
В тех случаях, когда число испытаний 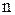 велико, а вероятность велико, а вероятность  мала пользуются формулой Пуассона: мала пользуются формулой Пуассона:
 , где , где  среднее число появлений события в различных сериях испытаний.
Вероятность того, что в среднее число появлений события в различных сериях испытаний.
Вероятность того, что в 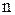 независимых испытаниях ( независимых испытаниях (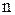 велико) событие наступит не менее велико) событие наступит не менее  раз и не более раз и не более  раз, приближенно равна раз, приближенно равна
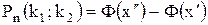 ,
где ,
где 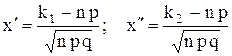 .
Функция .
Функция  определяется формулой определяется формулой  . Функция Лапласа нечетная, то есть . Функция Лапласа нечетная, то есть 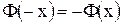 .
Последняя формула носит название интегральной теоремы Лапласа. Она тем точнее, чем больше значение .
Последняя формула носит название интегральной теоремы Лапласа. Она тем точнее, чем больше значение 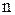 . .
| Задача.
Монета брошена 4 раза. Тогда вероятность того, что орел выпадет хотя бы один раз, равна …
Варианты ответов: 1) 1/16 2) 1/2 3) 3/4 4) 15/16
Решение.
Так как в условии присутствует фраза “ хотя бы один раз ”, то решаем “от противного” и найдем вероятность того, что при 4 бросаниях орел не выпадет ни разу.
Применим формулу Бернулли, т.к. испытания независимы и вероятность события “выпадение орла” остается в каждом опыте неизменной и равной 1/2.
Тогда искомая вероятность равна
 .
Ответ. №4.
Задача.
В лаборатории проводится серия из 400 опытов по обнаружению микроба в растворе. Вероятность появления микроба в каждом отдельном опыте равно 0,2. Найти вероятность того, что микроб будет обнаружен в 80 опытах.
Решение.
Очевидно, что при .
Ответ. №4.
Задача.
В лаборатории проводится серия из 400 опытов по обнаружению микроба в растворе. Вероятность появления микроба в каждом отдельном опыте равно 0,2. Найти вероятность того, что микроб будет обнаружен в 80 опытах.
Решение.
Очевидно, что при 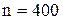 пользоваться формулой Бернулли практически невозможно из-за необходимости вычислять факториалы больших чисел. Воспользуемся локальной теоремой Лапласа. Итак, пользоваться формулой Бернулли практически невозможно из-за необходимости вычислять факториалы больших чисел. Воспользуемся локальной теоремой Лапласа. Итак,  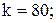 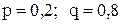 ; ;  .
Найдем значение функции .
Найдем значение функции  по таблице: по таблице:  . .
 .
Задача.
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение.
По условию .
Задача.
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение.
По условию 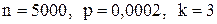  велико; велико; 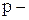 мало. Найдем мало. Найдем 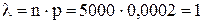 .
По формуле Пуассона искомая вероятность приближенно равна .
По формуле Пуассона искомая вероятность приближенно равна 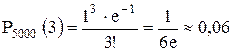 . .
| |||||||||
| §7 Случайная величина и ее числовые характеристики | ||||||||||
Случайной величиной называется величина, которая в результате опыта может принять какое-либо числовое значение, заранее нам не известное.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
Существует универсальный способ задания закона распределения, который годится для случайных величин любого типа: функцией распределения случайной величины  называется функция называется функция  , равная вероятности того, что , равная вероятности того, что  примет значение меньше, чем число примет значение меньше, чем число  , то есть , то есть  . Иногда ее называют интегральной функцией распределения.
Из определения следует: . Иногда ее называют интегральной функцией распределения.
Из определения следует:  и и 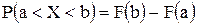 .
Непрерывную случайную величину можно также задать, используя другую функцию .
Непрерывную случайную величину можно также задать, используя другую функцию 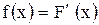 , которую называют плотностью распределения вероятностей (иногда ее называют дифференциальной функцией).
Из определения следует: , которую называют плотностью распределения вероятностей (иногда ее называют дифференциальной функцией).
Из определения следует:
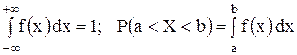 .
Одна из числовых характеристик, фиксирующая положение случайной величины на числовой оси, то есть некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения – математическое ожидание .
Одна из числовых характеристик, фиксирующая положение случайной величины на числовой оси, то есть некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения – математическое ожидание 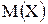 .
Математическое ожидание вычисляется: .
Математическое ожидание вычисляется:
 для дискретной случайной величины; для дискретной случайной величины;
 для непрерывной случайной величины.
Дисперсия для непрерывной случайной величины.
Дисперсия  есть характеристика рассеяния, разбросанности случайной величины около ее математического ожидания.
Дисперсия вычисляется: есть характеристика рассеяния, разбросанности случайной величины около ее математического ожидания.
Дисперсия вычисляется:
 для дискретной случайной величины; для дискретной случайной величины;
 для непрерывной случайной величины.
Иногда дисперсию удобно вычислять по следующей формуле: для непрерывной случайной величины.
Иногда дисперсию удобно вычислять по следующей формуле:  Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому вводится еще одна характеристика рассеяния – среднее квадратическое отклонение
Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому вводится еще одна характеристика рассеяния – среднее квадратическое отклонение
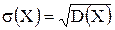 Математическое ожидание обладает следующими свойствами:
1.
Математическое ожидание обладает следующими свойствами:
1. 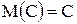 , где , где 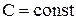 ;
2. ;
2.  , где , где 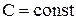 ;
3. ;
3.  ;
4. ;
4. 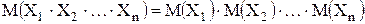 , если , если  - взаимно независимые случайные величины.
Дисперсия обладает следующими свойствами:
1. - взаимно независимые случайные величины.
Дисперсия обладает следующими свойствами:
1.  , где , где 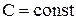 ;
2. ;
2. 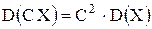 , где , где 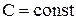 ;
3. ;
3. 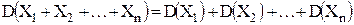 , если , если
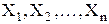 - независимые случайные величины. - независимые случайные величины.
| Задача.
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
Тогда математическое ожидание этой случайной величины равно… Решение. По определению Ответ. №2.
|
Задача.
Дискретная случайная величина задана законом распределения вероятностей
| X | -1 | ||
| P | 0,1 | a | b |
Тогда ее математическое ожидание равно 3,3 если …
Варианты ответов: 1) a=0,1; b=0,8 2) a=0,8; b=0,1
3) a=0,1; b=0,9 4) a=0,2; b=0,7
Решение.
Используем формулы  и
и  .
.
Составим систему
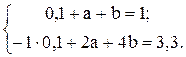
Решая ее, получаем a=0,1; b=0,8.
Ответ. №1
Задача.
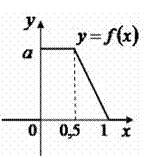
График плотности распределения вероятностей 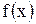 случайной величины приведен на рисунке.
случайной величины приведен на рисунке.
 |
Варианты ответов: 1)
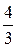 2) 1,2 3) 0,9 4)
2) 1,2 3) 0,9 4) 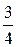
Решение.
Согласно свойствам функции 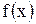 , площадь фигуры, ограниченной графиком
, площадь фигуры, ограниченной графиком 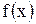 и осью
и осью  , всегда равна 1. Вычисляем площадь трапеции
, всегда равна 1. Вычисляем площадь трапеции
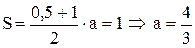 .
.
Ответ. №1.




 элементов и расположить эти
элементов и расположить эти  элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из
элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из 


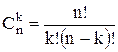
 .
.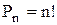

 числа появлений события в
числа появлений события в  , а соответствующие вероятности вычисляются по формуле Бернулли:
, а соответствующие вероятности вычисляются по формуле Бернулли:
 .
Случайная величина
.
Случайная величина 
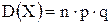 .
.
 График функции плотности вероятности для биномиального распределения
Предельным для биномиального, когда число
График функции плотности вероятности для биномиального распределения
Предельным для биномиального, когда число  , где
, где  Для данного закона распределения
Для данного закона распределения 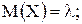
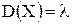 .
.
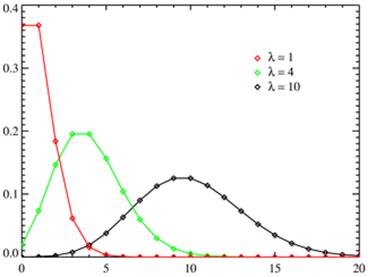 График функции плотности вероятности для закона Пуассона
Геометрическимназывается закон распределения дискретной случайной величины
График функции плотности вероятности для закона Пуассона
Геометрическимназывается закон распределения дискретной случайной величины  . Ее возможные значения
. Ее возможные значения  а соответствующие вероятности
а соответствующие вероятности
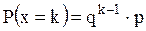 .
Для геометрического распределения
.
Для геометрического распределения
 .
.
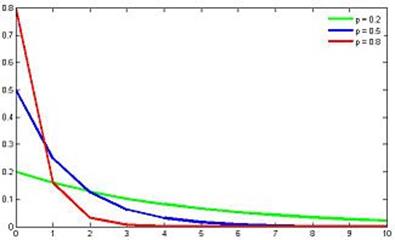 График функции плотности вероятности для геометрического распределения
Случайная величина
График функции плотности вероятности для геометрического распределения
Случайная величина 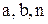 , если ее возможные значения
, если ее возможные значения  а имеют вероятности:
а имеют вероятности:
 .
Гипергеометрическое распределение возникает при следующих условиях: имеется урна, в которой
.
Гипергеометрическое распределение возникает при следующих условиях: имеется урна, в которой 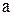 белых и
белых и  черных шаров, из нее вынимается
черных шаров, из нее вынимается 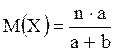 ;
;
 .
Однако, для гипергеометрического распределения иногда числовые характеристики удобнее вычислять по определению.
.
Однако, для гипергеометрического распределения иногда числовые характеристики удобнее вычислять по определению.
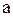 до
до 
 График функции плотности вероятности для равномерного распределения
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
График функции плотности вероятности для равномерного распределения
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
 где
где 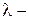 постоянная положительная величина. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
постоянная положительная величина. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
 График функции плотности вероятности для показательного распределения
Часто длительность времени безотказной работы элементы
График функции плотности вероятности для показательного распределения
Часто длительность времени безотказной работы элементы  имеет показательное распределение, функция распределения которого
имеет показательное распределение, функция распределения которого
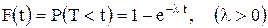 определяет вероятность отказа элемента за время длительностью
определяет вероятность отказа элемента за время длительностью  .
.  интенсивность отказов (среднее число отказов в единицу времени).
Нормальный закон распределения (закон Гаусса) Плотность распределения нормального закона имеет вид
интенсивность отказов (среднее число отказов в единицу времени).
Нормальный закон распределения (закон Гаусса) Плотность распределения нормального закона имеет вид
 ,
где
,
где 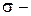 среднее квадратическое отклонение
среднее квадратическое отклонение  График функции плотности вероятности для нормального распределения
Вероятность того, что нормально распределенная СВ
График функции плотности вероятности для нормального распределения
Вероятность того, что нормально распределенная СВ  , вычисляется по формуле:
, вычисляется по формуле:
 ,
где
,
где  функция Лапласа.
Вероятность того, что отклонение нормально распределенной случайной величины
функция Лапласа.
Вероятность того, что отклонение нормально распределенной случайной величины  , вычисляется по формуле
, вычисляется по формуле
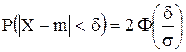 .
.
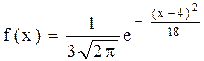 . Тогда математическое ожидание этой нормально распределенной случайной величины равно …
Варианты ответов: 1) 4 2) 9 3) 18 4) 3
Решение.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
. Тогда математическое ожидание этой нормально распределенной случайной величины равно …
Варианты ответов: 1) 4 2) 9 3) 18 4) 3
Решение.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
 .
Очевидно, что нормальное распределение определяется двумя параметрами: а и s, где а есть математическое ожидание, s - среднее квадратическое отклонение нормального распределения.
Поэтому а=4.
Ответ. №1.
Задача.
Математическое ожидание и среднее квадратического отклонение нормально распределенной случайной величины
.
Очевидно, что нормальное распределение определяется двумя параметрами: а и s, где а есть математическое ожидание, s - среднее квадратическое отклонение нормального распределения.
Поэтому а=4.
Ответ. №1.
Задача.
Математическое ожидание и среднее квадратического отклонение нормально распределенной случайной величины  .
Подставив
.
Подставив 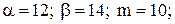
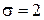 , получим
, получим
 .
По таблице находим
.
По таблице находим  .
Искомая вероятность
.
Искомая вероятность 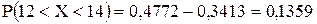 .
.
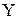 , то
, то  .
Рассмотрим правила для нахождения закона распределения СВ
.
Рассмотрим правила для нахождения закона распределения СВ 
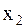

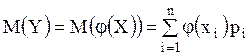 .
.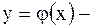 дифференцируемая строго монотонная, обратная функция которой
дифференцируемая строго монотонная, обратная функция которой  , то плотность распределения
, то плотность распределения 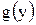 случайной величины
случайной величины  .
.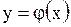 в интервале возможных значений
в интервале возможных значений 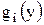 для каждого из интервалов монотонности, а затем представить
для каждого из интервалов монотонности, а затем представить  .
.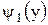 и
и 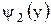 , то
, то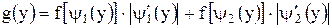

 или
или 
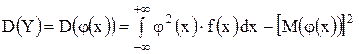 .
.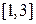 . Тогда случайная величина Y=3X+1 имеет…
Варианты ответов:
1) нормальное распределение на отрезке
. Тогда случайная величина Y=3X+1 имеет…
Варианты ответов:
1) нормальное распределение на отрезке  2) равномерное распределение на отрезке
2) равномерное распределение на отрезке  3) другой (кроме равномерного и нормального) вид распределения
4) нормальное распределение на отрезке
3) другой (кроме равномерного и нормального) вид распределения
4) нормальное распределение на отрезке  и ее математическое ожидание.
и ее математическое ожидание.
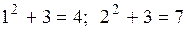 .
.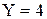 , соответствуют возможные значения
, соответствуют возможные значения  и
и 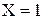 , поэтому
, поэтому  . Вероятности возможных значений
. Вероятности возможных значений ;
; 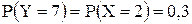 .
.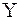


 .
.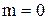 и
и  . Найти закон распределения СВ
. Найти закон распределения СВ  .
.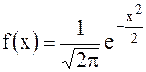 .
.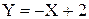 , то
, то 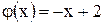 . Найдем для
. Найдем для  ;
;