1. Статистическая гипотеза. Виды гипотез.
2. Проверка статистических гипотез.
3. Общая схема построения критерия.
4. Основные типы гипотез
1.
Обычно в практических задачах не встречаются случайные величины, распределения которых точно соответствовали бы теоретическим распределениям. Последние являются математическими моделями реальных распределений. Подбор таких моделей и анализ их адекватности моделируемым случайным величинам, что является одной из основных задач математической статистики, которая, в свою очередь, сводится к проверке предположений (гипотез) о виде модели распределения и его параметрах.
Статистическая гипотеза – это некоторое предположение относительно генеральной совокупности, проверяемое по выборочным данным (или, другими словами, любое предположение о виде неизвестного закона распределения или параметрах известного закона распределения).
Гипотеза называется параметрической, если в ней содержится некоторое утверждение о значении параметра распределения известного вида или сравнительной величине параметров двух распределений. Параметрические гипотезы формулируются на основании тех или иных статистических законов распределения и могут использоваться лишь в том случае, если распределение выборочных данных согласуется с этим законом распределения.
В непараметрической гипотезе заключается утверждение о виде распределения. Непараметрические гипотезы применяются в том случае, если закон распределения изучаемых случайных величин неизвестен или их распределение не соответствует никакому из известных законов. В этом случае необходимо проверить, согласуются ли выборочные (эмпирические) данные с каким-либо теоретическим распределением или нет. Чаще всего проверяют гипотезу о соответствии выборочных данных нормальному распределению.
Гипотезы подразделяются на простые и сложные.
Параметрическая гипотеза называется простой, если в ней речь идет ровно об одном значении параметра (одномерного или многомерного), например, «Среднедушевой совокупный доход населения России составляет 10500 руб. в месяц»; «Уровень безработицы (доля безработных в численности экономически активного населения) в России равен 9%». В других случаях гипотеза называется сложной (т.е. гипотеза, состоящая ин некоторого числа простых гипотез), например, «вероятность появления события в схеме Бернулли заключена между 0,3 и 0,6», «закон распределения не является нормальным».
По своему содержанию статистические гипотезы можно подразделить на несколько основных типов:
1) Гипотезы о виде закона распределения исследуемой случайной величины;
2) Гипотезы о числовых значениях параметров исследуемой генеральной совокупности;
3) Гипотезы об однородности двух или нескольких выборок или некоторых характеристик анализируемых совокупностей;
4) Гипотезы об общем виде модели, описывающей статистическую зависимость между признаками; и др.
2.
Сопоставление высказанной гипотезы относительно генеральной совокупности с имеющимися выборочными данными, сопровождаемое количественной оценкой степени достоверности получаемого вывода и осуществляемое с помощью того или иного статистического критерия, называется проверкой статистических гипотез.
Выдвинутая гипотеза называется нулевой (основной). Ее принято обозначать Н0.
По отношению к высказанной (основной) гипотезе всегда можно сформулировать альтернативную (конкурирующую), противоречащую ей. Альтернативную (конкурирующую) гипотезу принято обозначать Н1.
Цель статистической проверки гипотез состоит в том, чтобы на основании выборочных данных принять решение о справедливости основной гипотезы Н0.
Так как проверка статистических гипотез осуществляется на основании выборочных данных, т.е. ограниченного ряда наблюдений, решения относительно нулевой гипотезы Н0 имеют вероятностный характер. Другими словами, такое решение неизбежно сопровождается некоторой, хотя возможно и очень малой, вероятностью ошибочного заключения как в ту, так и в другую сторону.
Так, в какой-то небольшой доле случаев α нулевая гипотеза Н0 может оказаться отвергнутой, в то время как в действительности в генеральной совокупности она является справедливой. Такую ошибку называют ошибкой 1-го рода, а ее вероятность – уровнем значимости и обозначают α.
Наоборот, в какой-то небольшой доле случаев β нулевая гипотеза Н0 принимается, в то время как на самом деле в генеральной совокупности она ошибочна, а справедлива альтернативная гипотеза Н1. Такую ошибку называю ошибкой 2-го рода. Вероятность ошибки 2-го рода обозначается как β. Вероятность 1-β называют мощностью критерия.
В ряде прикладных исследований ошибка первого рода α означает вероятность того, что предназначавшийся наблюдателю сигнал не будет им принят, а ошибка второго рода β – вероятность того, что наблюдатель примет ложный сигнал.
При фиксированном объеме выборки можно выбрать по своему усмотрению величину вероятности только одной из ошибок α или β. Увеличение вероятности одной из них приводит к снижению другой. Принято задавать вероятность ошибки 1-го рода α – уровень значимости. Как правило, пользуются некоторыми стандартными значениями уровня значимости α: 0,1; 0,05; 0,01. Тогда, очевидно, из двух критериев, характеризующихся одной и той же вероятностью α (отклонить правильную в действительности гипотезу Н0), следует принять тот, которому соответствует меньшая ошибка 2-го рода β, т.е. большая мощность. Снижения вероятностей обеих ошибок α и β можно добиться путем увеличения объема выборки.
Правильное решение относительно нулевой гипотезы Н0 также может быть двух видов:
– будет принята нулевая гипотеза Н0, когда в генеральной совокупности верна нулевая гипотеза Н0; вероятность такого решения 1-α;
– нулевая гипотеза Н0 будет отклонена в пользу альтернативной, когда в генеральной совокупности нулевая гипотеза отклоняется в пользу альтернативной Н1; вероятность такого решения 1-β – мощность критерия.
Обобщим сказанное в таблице:
| Гипотеза Но | Принимается | Отвергается |
| Верна | Правильное решение 1-α=Р(Но/Но) | Ошибка 1-го рода α=Р(Н1/Но) |
| Неверна | Ошибка 2-го рода β=Р(Но/Н1) | Правильное решение 1-β=Р(Н1/Н1) |
3.
Проверка статистических гипотез осуществляется с помощью статистического критерия (назовем его в общем виде θ), являющегося функцией от результатов наблюдений.
Статистический критерий – это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н0.
Значения критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия (θнабл).
Значения критерия, разделяющие совокупность значений критерия на область допустимых значений и критическую область, определяемые на заданном уровне значимости α по таблица распределения случайной величины θ, выбранной в качестве критерия, называются критическими точками (θкр).
Областью допустимых значений (областью принятия нулевой гипотезы Н0) называют совокупность значений критерия θ, при которых нулевая гипотеза Н0 не отклоняется.
Критической областью называют совокупность значений критерия θ, при которых нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Если конкурирующая гипотеза – правосторонняя, например, Н1:а>а0, то критическая область – правосторонняя. При правосторонней конкурирующей гипотезе критическая точка θкр.п принимает положительные значения. Вид правосторонней критической области:
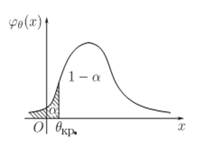
Если конкурирующая гипотеза – левосторонняя, например,Н1:а<а0, то и критическая область – левосторонняя. При левосторонней конкурирующей гипотезе критическая точка принимает отрицательные значения (θкр.л). Вид левосторонней критической области:
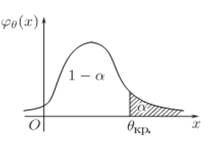
Если конкурирующая гипотеза – двусторонняя, например,Н1:а≠а0, то и критическая область – двусторонняя. При двусторонней конкурирующей гипотезе определяются две критические точки (θкр.л. и θкр.п.). Вид двусторонней критической области следующий:
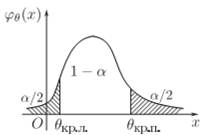
Основной принцип проверки статистических гипотез состоит в следующем:
– если наблюдаемое значение критерия (θнабл) принадлежит критической области, то нулевая гипотеза θ0 отклоняется в пользу конкурирующей Н1;
– если наблюдаемое значение критерия принадлежит области допустимых значений, то нулевую гипотезу Н0 нельзя отклонить.
Можно принять решение относительно нулевой гипотезы Н0 путем сравнения наблюдаемого и критического значений критерия.
При правосторонней конкурирующей гипотезе:
– если θнабл≤θкр, то нулевую гипотезу Н0 нельзя отклонить;
– если θнабл>θкр, то нулевая гипотеза отклоняется в пользу конкурирующей Н1.
При левосторонней конкурирующей гипотезе:
– если θнабл≥- θкр, то нулевую гипотезу Н0 нельзя отклонить;
– если θнабл<-θкр, то нулевая гипотеза отклоняется в пользу конкурирующей Н1.
При двусторонней конкурирующей гипотезе:
– если –θкр≤ θнабл≤θкр, то нулевую гипотезу Н0 нельзя отклонить;
– если θнабл>θкр или θнабл<-θкр, то нулевая гипотеза отклоняется в пользу конкурирующей Н1.
Если закон распределения статистики θ, вычисленной в предположении, что нулевая гипотеза верна, известен, то критические значения статистики могут быть найдены из условий:
- для правосторонней критической области 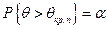
- для левосторонней критической области 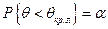
- для двусторонней критической области 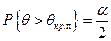 ,
, 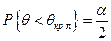
Алгоритм проверки статистических гипотез сводится к следующему:
1) Сформулировать нулевую Н0 и альтернативную Н1 гипотезы;
2) Выбрать уровень значимости α;
3) В соответствии с видом выдвигаемой нулевой гипотезы Н0 выбрать статистический критерий для ее проверки, т.е. – специально подобранную случайную величину θ, точное или приближенное распределение которой заранее известно;
4) По таблицам распределения случайной величины θ, выбранной в качестве статистического критерия, найти критическое значение θкр (критическую точку или точки);
5) На основании выборочных данных по специальному алгоритму вычислить наблюдаемое значение критерия θнабл;
6) По виду конкурирующей гипотезы Н1 определить тип критической области (ту критическую область, при которой мощность критерия будет больше);
7) Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия θнабл, и в зависимости от этого – принять решение относительно нулевой гипотезы Н0.
Следует заметить, что даже в том случае, если нулевую гипотезу Н0 нельзя отклонить, это не означает, что высказанное предположение о генеральной совокупности является единственно подходящим: просто ему не противоречат имеющиеся выборочные данные, однако таким же свойством наряду с высказанной могут обладать и другие гипотезы.
Можно интерпретировать результаты проверки нулевой гипотезы следующим образом:
– если в результате проверки нулевую гипотезу Н0 нельзя отклонить, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью отклонить нулевую гипотезу Н0, вероятность нулевой гипотезы Н0 дольше α, а конкурирующая Н1 – меньше 1-α;
– если в результате проверки нулевая гипотезы Н0 отклоняется в пользу конкурирующей Н1, то имеющиеся выборочные данные не позволяют с достаточной уверенностью принять нулевую гипотезу Н0, вероятность нулевой гипотезы Н0 меньше α, а конкурирующей Н1 – больше 1-α.
4.
По своему прикладному содержанию статистические гипотезы можно подразделить на несколько основных типов:
1) О числовых значениях параметров (таблица);
2) О равенстве числовых характеристик генеральной совокупности (таблица);
3) О законе распределения;
4) Об однородности выборок (т.е. принадлежности их одной и той же генеральной совокупности)
Таблица 1. Критерии о числовых значениях параметров
| Предположения | Статистика критерия | 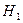
| Критерий отклонения гипотезы 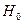
|
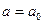
| 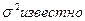
| 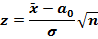
| 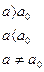
| 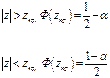
|
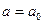
| 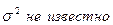
| 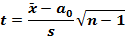
| 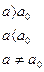
| 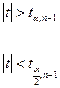 
|
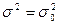
| 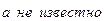
| 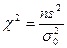
| 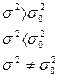
| 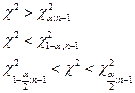
|
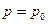
| n порядка нескольких десятков или сот, 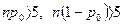
| 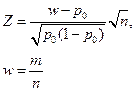
| 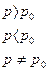
| 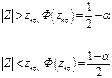
|
Таблица 2. О равенстве числовых характеристик генеральной совокупности
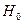
| Предположения | Статистика критерия | 
| Область принятия 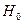
|

|  и и 
| 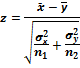
| 
| 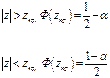
|

|  и и  но равны
но равны
| 

| 
| 
|

| 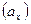 и и 

| 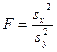 ,
где ,
где 
| 

| 
|

| n порядка нескольких десятков или сотен, 
| 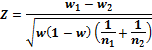 
| 
| 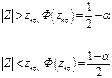
|