Конспект урока
Алгебра и начала математического анализа
Тригонометрические неравенства.
Перечень вопросов, рассматриваемых в теме
- решение простейших тригонометрических неравенств с помощью тригонометрической окружности;
- решение тригонометрических неравенств, сводимых к квадратным;
- решение тригонометрических неравенств методом интервалов.
Глоссарий по теме
- Синусом угла
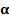называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол 
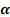.Обозначается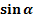 
- Косинусом угла 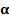называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол 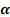.Обозначается
- Тангенсом угла 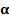называется отношение 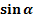к
Угол 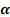может выражаться и в градусах и в радианах.
- Арккосинусом числа
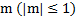называется такое число α, что: 
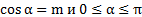. Арккосинус числа m обозначают: 
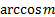. - Арксинусом числа
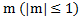называется такое число α, что: 
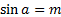и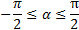 
. Арксинус числа m обозначают: 
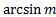. - Арктангенсом числа m называется такое число α, что:
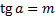и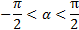 
. Арктангенс числа m обозначают: 
.
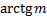Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
1. Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства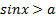 
.
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
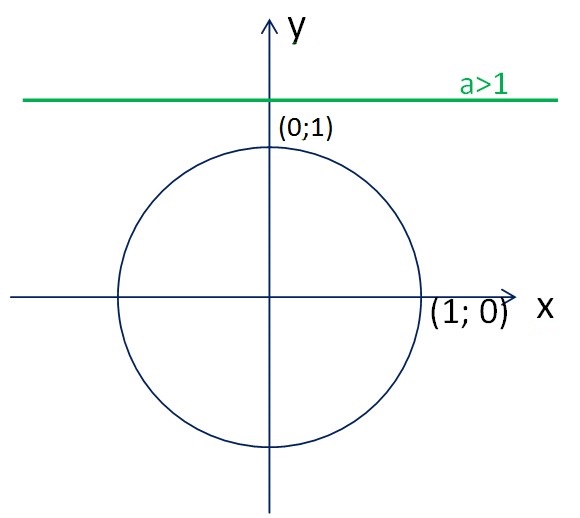
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на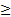 
(получим неравенство 
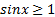, то решением его будет множество точек, в которых 
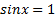. Это числа 
.
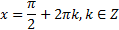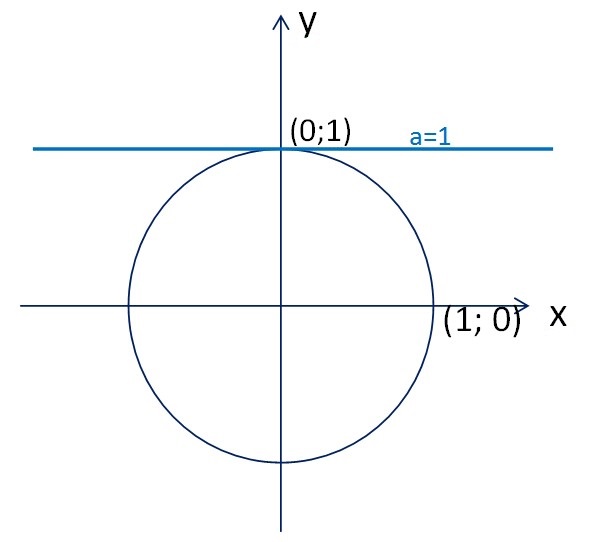
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
Рассмотрим теперь значение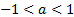 
(рис.3).
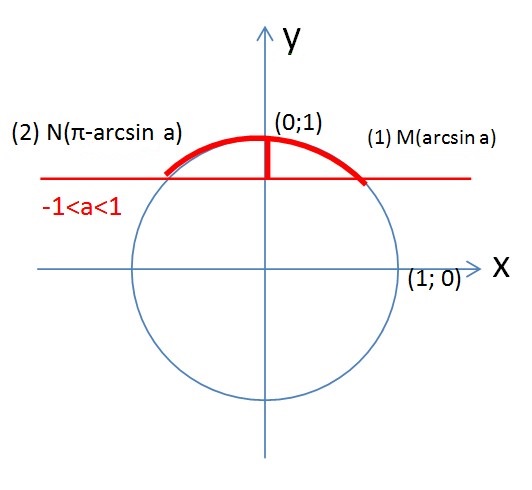
Рисунок 3 – Решение неравенства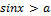 
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1)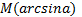 
, конец в точке (2) N(π – arcsina). В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением 
:
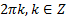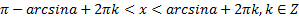
(для строгого неравенства) – множество интервалов;
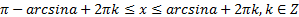
(для нестрогого неравенства) – множество отрезков.
Если значение a= – 1,то получим следующую картинку (рис. 4):
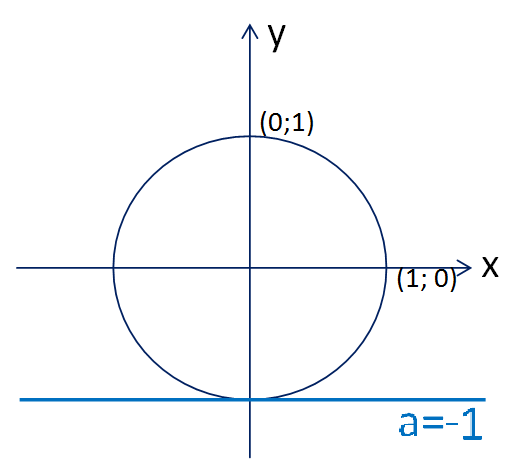
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства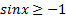 
является любое действительное число. Если неравенство строгое, то решением неравенства 
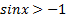является любое действительное число, кроме чисел вида 
.
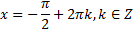Наконец, если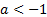 
, то решением неравенства 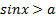является любое действительное число.
Решение неравенства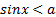 
рассмотрим более коротко.
Очевидно, что если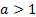 
, то решением неравенства 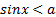является любое действительное число.
Если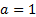 
, то решением неравенства 
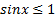является любое действительное число, а решением неравенства 
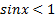является любое действительное число, за исключением чисел вида .
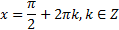Если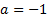 
, то решением неравенства 
являются числа вида 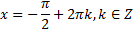, а неравенство 
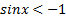решений не имеет. То же самое можно сказать о решении неравенств 
и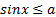 
в случае .
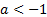Случай 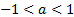рассмотрим более подробно (рис. 5).
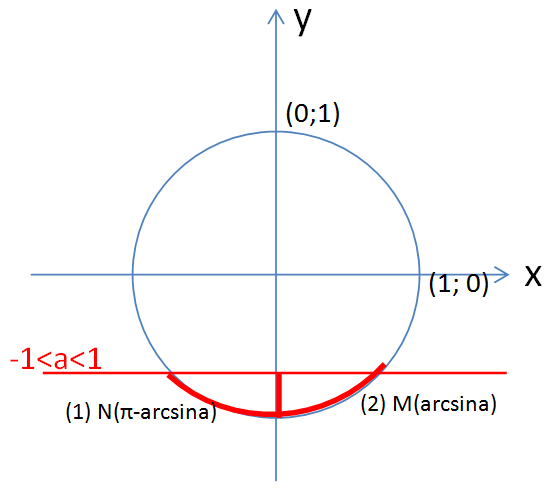
Рисунок 5 – Решение неравенства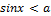 
Решение неравенства 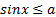для :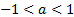
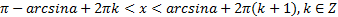(для строгого неравенства) - множество интервалов;
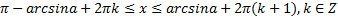(для нестрогого неравенства) - множество отрезков.