1.1. Распространение «свободных» электромагнитной волн типа Е и волн типа Н в планарном диэлектрическом волноводе на металлической подложке.
Изучим "свободные"электромагнитные процессы в системе, состоящей из диэлектрической пластины толщиной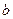 
и идеально проводящего основания 
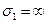(рис. 1.1). Волновод является бесконечно протяженным в направлении оси 
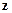, а также оси 
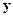, перпендикулярной плоскости 
.
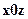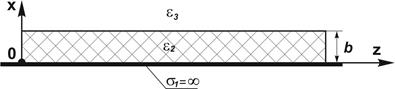
Рис 1.1. Планарный диэлектрический волновод на металлической подложке
Относительная диэлектрическая проницаемость материала пластины в области 2 (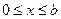
) и верхнего полупространства 3 (
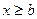) обозначены как 
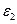и 
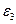соответственно. Далее для простоты будем считать, что диэлектрики немагнитные 
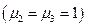и не имеют потерь 
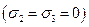. Диэлектрическая пластина имеет общую границу с металлической подложкой, являющейся идеальным проводником 
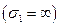в области 1 (- 
< 
).
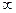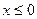Ограничимся случаем монохроматического поля с временной зависимостью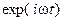 
, где 
– круговая частота. Для определения структуры электромагнитного поля "свободных" направляемых E–или H-волн диэлектрического волновода необходимо решить систему уравнений Максвелла при отсутствии сторонних источников. Выпишем первые два уравнения системы:
, 
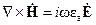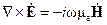, (1.1)
где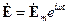 
, 
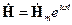–вектора напряжённости электрического и магнитного поля, 
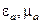– абсолютная диэлектрическая и магнитная проницаемость среды, с граничными условиями на поверхностях раздела 
, 
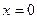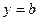и физическим условием убывания поля при 
.
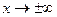В соответствии с геометрией задачи будем решать систему уравнений (1.1) в декартовой системе координат. Тогда каждое из уравнений системы (1.1) равносильно трем скалярным уравнениям:
; 
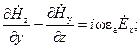
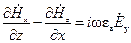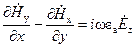(1.2)
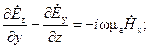
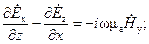
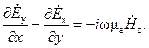(1.3)
В соответствии с методом комплексных амплитуд подставляя компоненты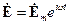 
и 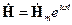, в (1.2), (1.3) и после сокращения на 
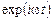получим уравнения для составляющих комплексных амплитуд 
, 
.
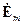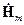Поскольку в направляющих линиях необходимо передавать энергию из одного сечения в другое в виде бегущих в направлении оси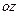 
волн, которые характеризуются множителем бегущей волны 
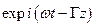, то аналогично случаю полых металлических волноводов решение (1.2), (1.3) для комплексных амплитуд 
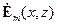и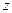 
в линии без потерь ищем в виде:
, 
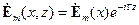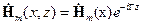, (1.4)
где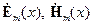 
- комплексные амплитуды, зависящие только от координаты 
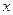и независимы от координаты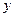 
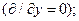Г,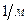 
– коэффициент распространения волны в рассматриваемой структуре.
После подстановки комплексных амплитуд (1.4) в уравнения (1.2) и в (1.3), последние разделяется на две следующие независимые подсистемы:
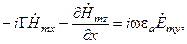
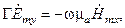
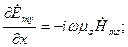(1.5)
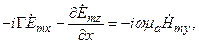
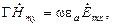
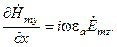(1.6)
Из анализа (1.5) и (1.6) следует, что для рассматриваемого случая, моды можно классифицировать по наличию (отсутствию) продольной (вдоль оси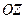 
) компоненты. Волны делятся на волны типа H: 
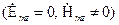, определяемые уравнением (1.5), для которых отличны от нуля только составляющие 
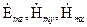, и на волны типа E: 
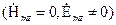, определяемые уравнением (1.6), для которых отличны от нуля только составляющие 
.
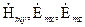Таким образом, для определения структуры возможных типов электромагнитных волн в диэлектрическом пленочном волноводе достаточно найти продольную (вдоль оси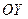 
) 
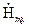– компоненту для H - волн или 
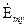-компоненту для E - волн, поскольку поперечные компоненты затем можно вычислить, используя (1.5) и (1.6). Кроме того, из уравнений (1.5), (1.6) видно, что для определения структуры электромагнитных волн в диэлектрическом волноводе удобно использовать компоненты 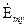– компоненту для H–волн и 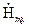–компоненту для E -волн.
Известно, что каждая из компонент электромагнитного поля во второй и третьей областях удовлетворяет однородному волновому уравнению
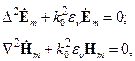(1.7)
с соответствующими граничными условиями на поверхностях разделов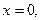 
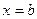и условию убывания поля при 
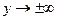; полагалось, что 
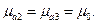В (1.7) 
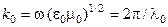– волновое число свободного пространства (
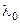– длина волны); 
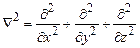– оператор Лапласа;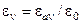 
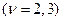– относительная диэлектрическая проницаемость сред.
1.2. Волны E-типа в планарном диэлектрическом волноводе на металлической подложке
Исключив составляющие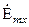 
и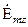 
из системы уравнений (1.6), для Е-волн приходим к последующим скалярным волновым уравнениям для 
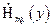второй среды:
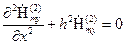, при 
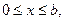(1.8)
где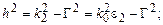 
и третьей среды
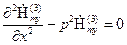, при 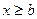, (1.9)
где 
Входящий в (1.9) параметр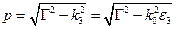 
для замедленных волн, у которых при 
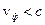, поперечное волновое число р является всегда действительным, в этом случае волна, удовлетворяющая (1.9), представляет гармоническую функцию и в области 
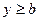убывает по экспоненциальному закону.
Общее решение уравнений (1.8) и (1.9) с учетом условия убывания поля в третьей среде при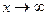 
имеет вид:
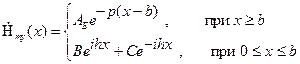(1.10)
Для определения комплексных постоянных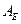 
, 
, 
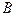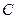и постоянных 
, 
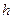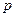воспользуемся граничными условиями для касательных составляющих поля на границах раздела двух сред. Тогда, учитывая, что первая среда (подложка) является идеальным проводником, получим:
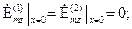
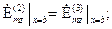
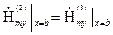. (1.11)
При этом в соответствии с (1.6)
, 
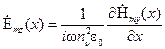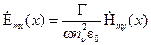, (1.12)
где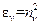 
, .
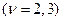Затем подставляя (1.12) в граничное условие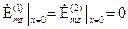 
и учитывая (1.10), получим 
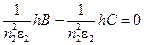, из которого следует 
.
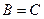Тогда общее решение (1.10) волнового уравнения принимает вид
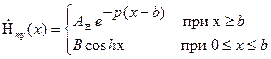, (1.13)
где 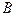– коэффициент, подлежащий определению.
Из двух оставшихся граничных условий, выполняемых при 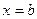в (1.11), получим 
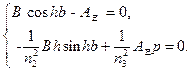(1.14)
Однородная система уравнений (1.14) имеет нетривиальное решение, т.е. при отличных от нуля коэффициентах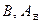 
, если выполнено условие
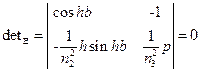. (1.15)
Раскрывая соотношение (1.15), получаем характеристическое уравнение для E– мод в планарном диэлектрическом волноводе на металлической подложке
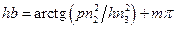, (1.16)
где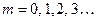 
– индекс моды.
Поскольку тангенс – функция периодическая с периодом, равным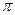 
, в правой части соотношения (1.16) появилось целое кратное числа 
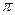. Таким образом, для заданной толщине диэлектрического волновода 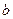существует множество решений (типов волн – мод) характеристического уравнения (1.16). Эти моды различаются индексом 
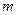, различными значениями поперечных волновых чисел , 
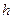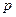и обозначаются как волны 
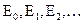и т.д.
Учитывая дополнительные соотношения, следующие из (1.8) и (1.9):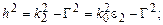 
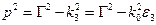, исключая в них постоянную распространения 
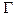, можно получить уравнение, связывающее параметры 
и 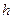в виде
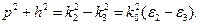. (1.17)
Объединяя (1.16) и (1.17) получим полную систему уравнений, определяющих значения поперечных волновых чисел и 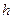для Е– мод:
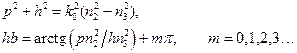(1.18)
Выражая из (1.14) 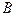через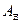 
и подставив их в (1.13), найдем найдём комплексные амплитуды составляющих Е–мод через произвольную комплексную амплитудную постоянную 
(зависит от параметров источника возбуждения, который на данном этапе не рассматривается) и поперечные волновые числа и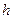 
:
; 
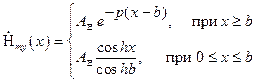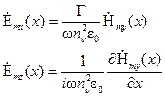, (1.19)
Определив из системы (1.18) величины и 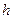, зависящие от толщины ДВ 
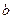и от коэффициентов преломления 
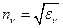сред, можно полностью рассчитать электромагнитное поле любой E –волны по формуле (1.19). Постоянная распространения 
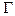волны для моды Еm для такой замедляющей структурой находится с помощью решения системы уравнений (1.18) и соотношений, следующих из (1.8) 
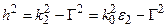и (1.9) 
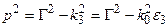, затем определяется длина волны в диэлектрическом волноводе 
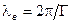и фазовая скорость 
.
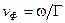Комплексная постоянная осталась не определённой, поскольку исследуются “свободные”, т.е. не зависящие от источника возбуждения, волны. Модуль и фаза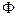 
постоянной 
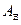зависят от амплитуды и фазы источника возбуждения. Используя (1.19) и учитывая (1.4), можно найти структуру E –мод в направлении распространения волн, например:
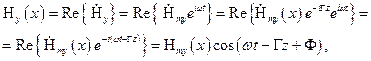
где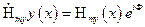 
. Откуда видно, что в фиксированный момент времени вдоль оси ДВ (направление распространения волны) распределение 
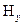–компоненты носит периодический характер с периодом, равным длине волны в диэлектрическом волноводе 
.
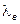Для изучения структуры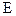 
- волн, характеризуемых числом 
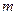и постоянной 
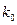, необходимо рассмотреть влияние параметров слоя на число корней характеристического уравнения в (1.18), определяющих значения продольного волнового числа 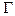. Для этого полную систему уравнений (1.18) после умножения на 
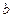преобразуем к виду
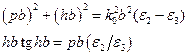, (1.20)
Система уравнений (1.20) включает алгебраическое уравнение второй степени и трансцендентное уравнение. Проведем анализ ее решения графическим методом. С этой целью построим графики указанных зависимостей (1.20) в координатах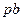 
и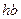 
для нескольких значений диэлектрической проницаемости 
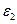слоя волновода (
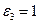), его толщины 
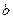и постоянной 
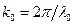. При построении указанных зависимостей, необходимых для графического решения системы уравнений (1.20), используется программирование в среде MathCAD [14].
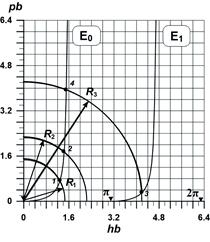
Рис. 1.2. Графический способ решения характеристического уравнения для Е-волн
Предварительно построим две кривые для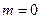 
и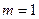 
, выбранных из бесконечного множества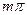 
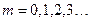, описываемого вторым уравнением (2.20), которые пересекают ось 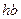в точках 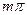. Точки пересечения ос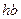и при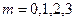 
отмечены символом 
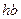(рис. 1.2). Заметим, что величины и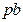 
являются положительными, поэтому графики функций изображены только в первом квадранте.
Нетрудно видеть, что первое уравнение (1.20) описывает семейство концентрических окружностей (рис. 1.2), с центром в начале координат, радиусы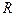 
которых зависят от диэлектрической проницаемости материала пластины, ее толщины и рабочей длины волны 
:
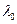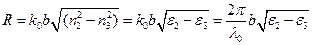. (1.21)
Точки на плоскости переменных 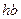и 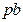в которых графики пересекаются (рис. 1.2) обозначены как 1, 2, 3, 4), соответствуют равенству левой и правой частей характеристического уравнения в (1.20), т.е. его корням.
Результаты решения графическим методом системы уравнений (1.20), представленные на рис.11.2, были получены для трех выбранных значений частоты и параметров слоя: №1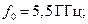 
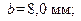
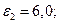№ 2, 
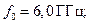
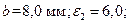№ 3,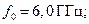 
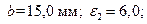во все трех примерах 
.
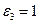Решения графическим методом системы уравнений (1.20) позволяет определить поперечные волновые числа и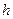 
, затем с учетом (1.8) или (1.9) рассчитать постоянную распространения 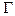, длину волны 
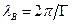и фазовую скорость 
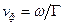электромагнитной волны (или волн) Е-типа распространяющейся в ДВ для каждого из трех примеров.
Для приведенных выше для трех примеров, согласно (1.21) рассчитаны радиусы окружностей :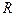 
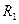=1,46; 
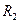=2,25; 
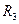=4,22. Из анализа графиков следует, что система уравнений (1.20), а значит (1.18) может иметь несколько решений. В частности, для окружности радиуса 
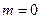=4,22, пересекающей две кривые в точках 3 и 4, описываемые вторым уравнением (1.20). Это означает, что уравнение (1.18) имеет два корня, определяемые при и 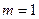, этом случае в ДВ могут одновременно распространяться две моды 
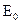и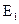 
. Кривая, определяемая при 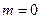, проходит через начало координат, поэтому при любом действительном значении 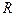, определяемом (1.21), всегда имеется решение уравнения (1.18). Значит при любом малом значении толщины 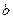диэлектрического слоя и любой частоте 
ДВ может распространяться мода 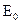при выполнении условия 
< 
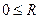, что выполняется для значени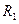й 
и 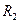(рис. 1.2). При выполнении условия < < 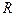2 в ДВ могут распространяться две моды 
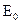и 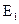, что выполняется для значения =4,22.
На рис. 1.2 построены две кривые для 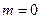и 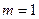, выбранные из бесконечного множества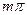 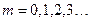, описываемого вторым уравнением (2.20), которые пересекают ось 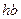в точках 
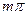, точки пересечения при 
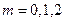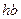отмечены символом . Заметим, что величины и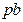 
являются положительными, поэтому графики функций изображены только в первом квадранте.
На основе проведенного анализа и геометрии, представленной на рис. 1.2, нетрудно сформулировать условие при котором в ДВ с известными параметрами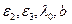 
возможно распространение 
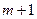числа Е-мод в виде
< 
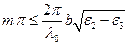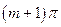. (1.22)
Значения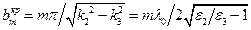 
соответствуют толщинам пластины ДВ, при которых могут возникать 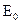, 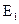волны и 
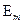волны высших типов.
Для оценки постоянной распространения 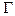, длины волны 
в ДВ и фазовой скорости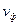 
поверхностной электромагнитной основной волны 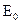воспользуемся результатами графического способа решения характеристического уравнения для примера №3 с учетом 
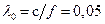м. Определяя значение безразмерного параметра 
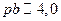для точки 4, откуда 
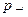266,7 м-1 [2,3]. Значение продольного волнового числа 
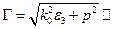294,8 м-1, длины волны в волноводе 
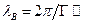0,0213 м и фазовой скорости 
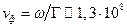м/с. Поскольку критическая толщинам пластины ДВ при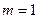 
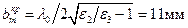меньше 
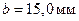, конечно в этом случае также выполняется условие (1.22), из которого следует, что в волноводе с параметрами 
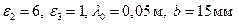возможно распространение волны 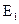. На рис. 1.3 представлен пример распределения нормированной магнитного составляющей "свободного" волнового поля основной волны 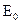, рассчитанной на основе (1.19) и программы MathCAD [14] (см. Приложение 4).
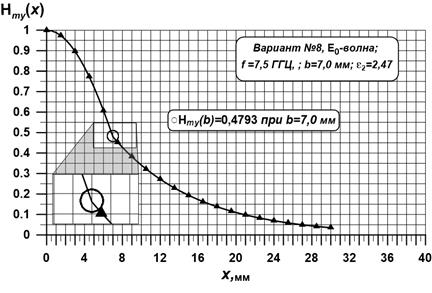
Рис. 1.3. Распределение нормированной магнитной составляющей основной волны .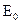
На рис. 1.3 центр символа в виде окружности совпадает с границей раздела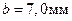 
, на увеличенном фрагменте виден излом составляющих 
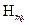магнитного поля на границе раздела. Угол излома зависимости распределения магнитной составляющей 
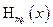на границе раздела определяется на основе (1.19) путем вычисления направления касательных к составляющей магнитного поля 
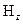слева и справа границы раздела пластина диэлектрика – свободное пространство.
На рис. 1.4 представлена структура силовых линий электромагнитного поля в диэлектрическом волноводе для примера №3. В этом случае выполнено условие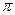 
< 
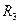< 2 
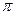в ДВ могут распространяться две моды 
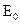и 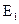(рис. 1.2) [2]. Картины силовых линий для волн высших типов могут быть построены аналогично на основе (11.19). Кроме того, в приведенных структурах силовых линий полей отражено уменьшение амплитуды поля при удалении точки наблюдения от поверхности ДВ вдоль оси 
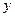, поскольку плотность силовых линий в этом направлении убывает. Силовые линии магнитного поля имеют лишь 
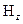компоненту и в силу двухмерности задачи "замкнуты" на бесконечности.
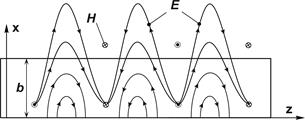
a)
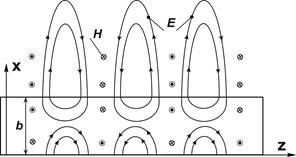
б)
Рис. 1.4. Структура силовых линий электромагнитного поля в диэлектрическом
волноводе: а) –волна 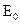; б) –волна .
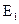При выполнении курсовой работы при заданных параметрах ДВ и типа основной моды, распространяющейся в волноводе и частоты проводят предварительные расчеты, включающие определение поперечных волновых чисел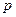 
и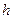 
на основе решения системы (1.18), определение продольного волнового числа 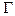, расчет нормированной составляющей 
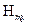, а также определение 
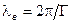и фазовой скорости 
.
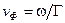1.3. Волны H-типа в планарном диэлектрическом волноводе на металлической подложке.
В диэлектрическом волноводе на идеально проводящей подложке помимо рассмотренных в п.1.2 Е-волн могут существовать волны H-типа, структура которых определяется уравнениями (1.5). По аналогии с пунктом 1.2. кратко рассмотрим свойства таких волн, отмечая отличия при определении структуры таких волн. Единственными ненулевыми составляющими поля в этом случае в соответствии с (1.5) будут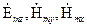 
. Снова решение ищется аналогично в виде (1.4):
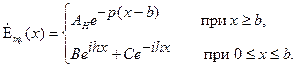(1.23)
Характеристическое уравнение (1.25) выводится как и для E-мод, но с использованием граничных условий для составляющих в (1.5)
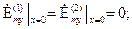
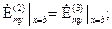
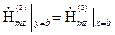. (1.24)
Таким образом, используя граничные условия (1.24) для решения (1.23) с учетом (1.5) можно получить характеристическое уравнение для Н-мод в виде
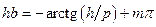, (1.25)
где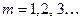 
– индекс моды.
Отметим, что в рассматриваемой структуре не может существовать волна типа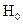 
(с индексом 
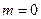), поскольку при выполнении граничных условий (1.24) при 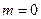уравнение (1.25) не имеет решения (см. рис. 1.6).
В этом случае соотношения между постоянным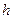и и 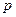связаны соотношением аналогичным (2.18) 
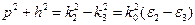. Тогда полная система уравнений, определяющих значения поперечных волновых чисел 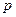и 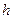для Н– мод:
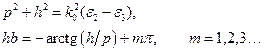(1.26)
Соответствующие компоненты электромагнитного поля для H-мод имеют вид:
; 
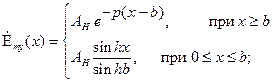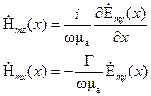. (1.27)
На рис. 1.5 представлен пример распределения нормированной электрической составляющей "свободного" волнового поля основной волны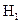 
, рассчитанной на основе (1.26) и (1.27) и программы MathCAD [5]. При 
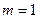значения параметров в (1.26) составили 
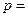100,524 м-1; 
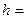221,811 м-1 (см. Приложение 4).
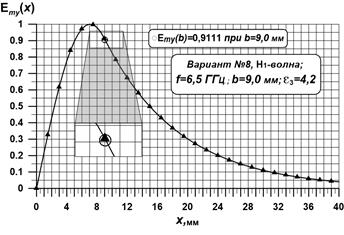
Рис. 1.5. Распределение нормированной электрической составляющей основной волны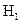 
.
На рис. 1.5 центр символа в виде окружности совпадает с границей раздела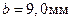 
, составляю щей 
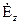на границе раздела пластина диэлектрика – свободное пространство для H-мод нет.
Проведение анализа решения системы уравнений для Н–мод (1.26) графическим методом, проведем аналогично решению системы (1.20). С этой целью построим графики указанных зависимостей (1.26) в координатах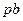 
и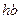 
для нескольких значений диэлектрической проницаемости 
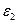слоя волновода (
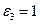), его толщины 
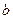и постоянной 
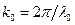. При построении указанных зависимостей, необходимых для графического решения системы уравнений (1.26), используется программирование в среде MathCAD.
Для построения графиков преобразуем (1.26) к виду
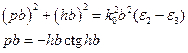, (1.28)
Результаты решения характеристического уравнения для Н-волн графическим методом проиллюстрируем на трех конкретных примерах, приняв следующие исходные данные частоты и параметров слоя: №1,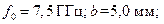 
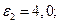№ 2, 
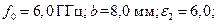№ 3,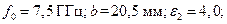 
во все трех примерах .
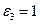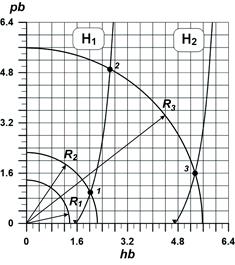
Рис. 1.6. Графический способ решения характеристического уравнения для Н-волн
Для данных, приведенных выше, согласно (2.26) и (2.28) на рис. 2.6 построены две кривые для 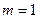и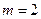 
из бесконечного множества 
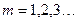, описываемого вторым уравнением (1.28), которые пересекают ось 
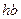в точках , точки пересечения при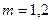 
отмечены символом , а также окружности которые имеют радиусы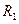 
=1,36; 
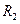=2,25; 
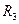=5,77. Из анализа графиков, представленных на рис. 1.6, следует, что уравнение (1.25) или (1.26) может не иметь решений, или одно или несколько решений, в частности для параметров примера №1 окружность радиуса 
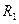=1,36 не пересекает ни одну из кривых, определяемых сомножителем 
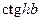в (1.28), т.е. система уравнений (1.28) не имеет решений при условии 
< 
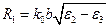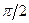и в ДВ не распространяются Н-моды. Значит Н-волны в направляющей системе появляются только при условии, что толщина диэлектрической пластины волновода 
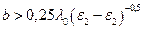. Для параметров примера №2 окружность радиуса 
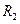=2,25 пересекает кривую в точке 1, в этом случае в ДВ при условии < < 
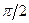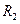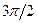может распространятся основная мода 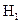(отметим, что согласно условию (1.21) в этих двух случаях в ДВ может распространяться основная мода 
).
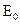На основе проведенного анализа и геометрии, представленной на рис.1.6, можно сформулировать условие, при котором в ДВ с известными параметрами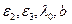 
, возможно распространение 
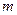числа Н-мод (
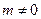) в виде
< 
< 
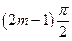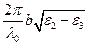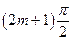. (1.29)
Для параметров приведенных для примера №3 окружность радиуса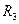 
=5,77 пересекает две кривые на рис. 1.6, описываемые вторым уравнением (2.26), в точках 2 и 3. В этом случае уравнение имеет два корня, определяемые пр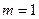и 
и 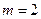, и в ДВ согласно условию (2.29)могут распространяться две моды 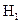и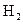 
, поскольку при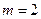 
< < 
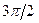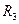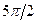. Отметим, что в этом случае наряду с модам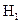и и 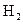в ДВ могут распространяться также две моды 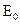и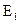 
(см. рис. 1.5) поскольку для значения 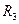=5,77 при 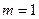выполняется условие (2.2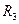2) 
< < 2 .
Контрольные вопросы (волна типа Е)
1. Записать систему уравнений Максвелла длябесконечного пространства и преобразования системы уравнений для определения структуры электромагнитного поля в планарном диэлектрическом волноводе на металлической подложке.
2. Записать систему уравнений Максвелла длябесконечного пространства с учетом сторонних источников.
3. Записать выражение для бегущей в направлении распространения волны в планарном диэлектрическом волноводе с учетом выбранной зависимости комплексной амплитуды волны.
4. Сформулировать граничные условия для касательных составляющих электрического и магнитного поля на границах планарного диэлектрического волновода на металлической подложке.
5. Сформулировать скалярное однородные волновое уравнения для Е-волн, пояснить метод решения уравнений с учетом граничных условий и условием убывания поля.
6. Записать однородные волновые уравнения и их решения для Е-волн для каждой из областей планарного диэлектрического волновода на металлической подложке.
7. Какие параметры планарного волновода и возбуждаемого волнового процесса определяют характеристики и структуру поверхностной волны в диэлектрической пластине планарного волновода?
8. Пояснить условие при котором в планарном диэлектрическом волноводе с известными параметрами возможно распространение заданного числа Е-мод.
9. Возможно ли выбрать параметры планарного диэлектрического волновода на металлической подложке и частоту волнового процесса, чтобы в волноводе распространялась лишь мода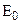 
?
10. Какова структура электромагнитного поля волны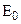 
?
Контрольные вопросы (волна типа Н)
1. Записать систему уравнений Максвелла длябесконечного про