Лекция 10. Связь между корреляционными функциями и спектральными плотностями случайных процессов на входе и выходе линейной САУ

План.

1.Постановка задачи для случая одного входного сигнала.

2.Связь между КФ на входе и выходе линейной САУ.

3.Связь между спектральными плотностями.

4.Случай двух входных воздействий.

Рассмотрим линейную систему автоматического управления (рис. 10.1), имеющую передаточную функцию W_gx (p  и импульсную переходную функцию (функцию веса) k(t).

Предположим, что на вход этой системы подан стационарный случайный процесс G(f), имеющий корреляционную функцию R_g(t) и спектральную плотность S_g (w). Если рассматриваемая линейная система устойчива и сама стационарна, то установившийся выходной сигнал X(t) также будет стационарным случайным процессом, однако его статистические характеристики будут отличаться от статистических характеристик входного сигнала.

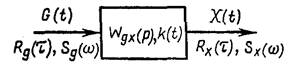
Рис 10.1

Допустим, что случайный процесс X(t) имеет корреляционную функцию R_x (t) и спектральную плотность S_x (w). Установим связь между корреляционными функциями и спектральными плотностями случайных процессовна входе и выходе системы. Связь между реализациями x(t) случайного процесса X(t) на выходе системы и соответствующими реализациями g(t) случайного процесса G(t) на входе системы на основании формулы свертки выражаетсячерез импульсную переходную функцию k(t) следующим образом:

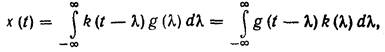(10.1)

где l — независимая переменная интегрирования. Для момента времени t+t получаем

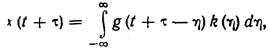(10.2)

где h — новое обозначение независимой переменной интегрирования. Корреляционная функция R_x (t) стационарного случайного процесса X(t) на

основании (??) равна

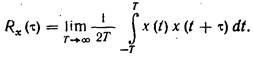(10.3)

Подставляя в (10.3) значение x(t) и x(t + t) иизменяя последовательность интегрирования, получим

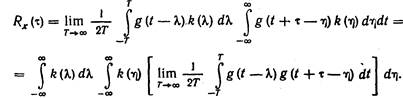(10.4)

Так как

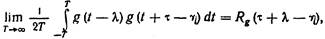
окончательно получаем

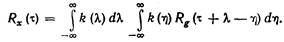(10.5)

Выражение (10.5) является основным интегральным соотношением, позволяющим по известной корреляционной функции R_g (t) случайного процесса на входе системы и известкой импульсной переходной функции k(t) системы найти корреляционную функцию R_x (t) случайного процесса на выходе системы.

Определим теперь связь между спектральными плотностями входного и выходного случайных процессов. В соответствии с (??) спектральная плотность случайного процесса X(t) на выходе системы

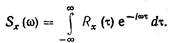(10.6)

Подставляя в (10.5) значение R_x (t) из (10.6), получаем

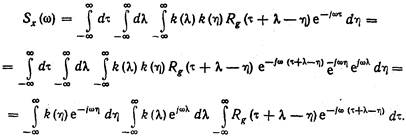(10.7)

Учитывая, что изображение Фурье импульсной переходной функции есть частотная передаточная функция, т. е.

(10.8)

выражение для спектральной плотности можно записать в виде

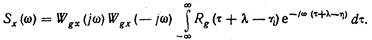(10.9)

Принимая во внимание, что

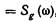
окончательно получаем

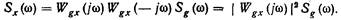(10.10)

Таким образом, спектральная плотность стационарного случайного процесса на выходе линейной системы равна спектральной плотности случайного процесса на входе системы, умноженной на квадрат модуля частотной передаточной функции этой системы.

Используя (??) и (10.10), можно найти формулу, связывающую корреляционную функцию R_x (t) выходного сигнала и спектральную плотность S_g (w) входного сигнала, т. е.

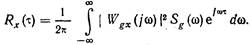(10.11)

Рассмотрим теперь более общий случай, когда линейная система находится под воздействием двух взаимосвязанных стационарных случайных процессов G(t) и F(t), приложенных в различных точкахсистемы.

Пусть передаточные функции, связывающие эти входные сигналы и выходной сигнал X(t), будут соответственно W ₁ (p) и W ₂ (p), а импульсные переходные функции (функции веса) k ₁ (t) и k ₂ (t). Покажем, как в этом случае связаны корреляционная функция R_x (t) и спектральная плотность S_x (w) выходного сигнала с корреляционными функциями и спектральными плотностями входных сигналов.

Задача о двух воздействиях имеет большое практическое значение, так как в большинстве случаев на систему действуют одновременно два входных сигнала: полезный сигнал и помеха. Заметим, что рассмотренная ниже методика может быть использована и в том случае, когда к системе приложено большее число воздействий.

В нашем случае реализация x(t) случайного процесса X(t) на выходе системы на основании принципа суперпозиции связана с реализациями g(t) и f(t) входных случайных процессов G(t) и F(t) следующим образом:

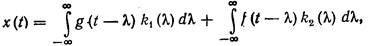(10.12)

где l — независимая переменная интегрирования. Для момента времени t + t получаем

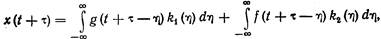(10.13)

где  — новое обозначение независимой переменной интегрирования. Подставляя (10.12) и (10.13) в (??), получаем

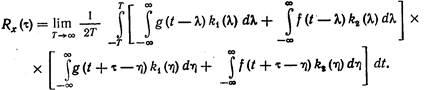(10.14)

Раскрывая скобки и меняя пределы интегрирования, получаем

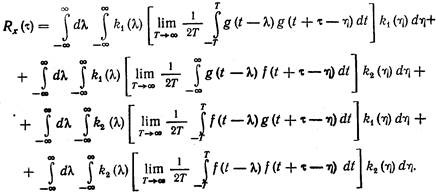(10.15)

Нетрудно заметить, что выражения, заключенные в квадратные скобки в первом и последнем слагаемых, равны корреляционным функциям R_g (t+l-h) и R_f (t+l-h) соответственно, а аналогичные выражения во втором и третьем слагаемых — взаимным корреляционным функциям R_gf (t+l-h) и R_fg (t+l-h).

Учитывая сказанное, окончательно находим

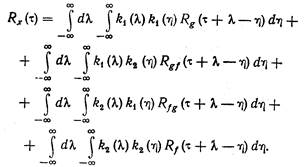(10.16)

Выражение (10.16) является основным интегральным соотношением, устанавливающим связь между корреляционной функцией R_x (t) выходного сигнала и четырьмя корреляционными функциями R_g (t), R_f (t), R_gf (t) и R_fg (t) двух статистически взаимосвязанных входных сигналов.

Найдем для этого случая спектральную плотность S_x (w) выходного сигнала. Подставляя (10.16) в (??), получим

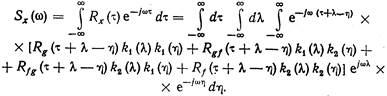(10.17)

Меняя порядок интегрирования, получаем

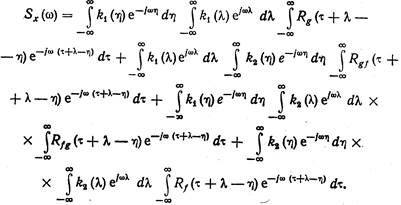(10.18)

Учитывая (10.14), формулу для спектральной плотности можно окончательно записать следующим образом:

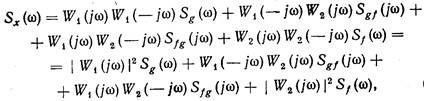(10.19)

где W_i (jw) — частотные передаточные функции, комплексно-сопряженные с W_i (jw).

В (10.19) величины

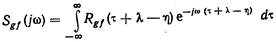
являются взаимными спектральными плотностями.

Формула (10.19) является выражением для спектральной плотности выходного сигнала для общего случая, когда система находится под воздействием двух статистически взаимосвязанных стационарных случайных процессов G(t) и F(t). Если случайные процессы G(t) и F(t) статистически независимы (корреляция между ними отсутствует), то

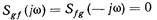(10.20)

и выражения для корреляционной функции и спектральной плотности выходного случайного процесса принимают вид:

(10.21)