Замечательные точки треугольника – это точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
Свойства точки, лежащей на биссектрисе неразвернутого угла:
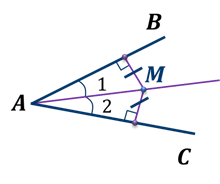
Теорема. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Обратная теорема. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
Теорема. Биссектриса неразвернутого угла есть геометрическое место точек, равноудаленных от сторон данного угла.

Биссектрисы треугольника пересекаются в одной точке.
 Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Свойства точки, лежащей на серединном перпендикуляре к отрезку:
 Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
 Теорема. Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.
Теорема. Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Медианы треугольника пересекаются в одной точке.

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Вписанная и описанная окружности
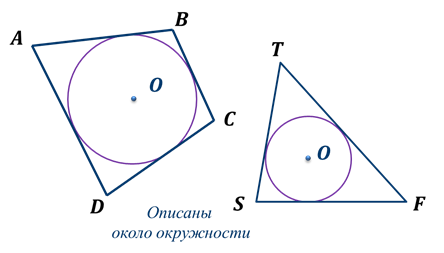 Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Теорема. В любой треугольник можно вписать окружность.
Замечания.
1. В треугольник можно вписать только одну окружность.
2. В отличие от треугольника не во всякий четырехугольник можно вписать окружность.
 Если в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
Если в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
В любом описанном четырехугольнике суммы противоположных сторон равны.

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Теорема. Около любого треугольника можно описать окружность.
Замечания.
1. Около любого треугольника можно описать только одну окружность.
2. В отличие от треугольника около четырехугольника не всегда можно описать окружность.
 Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
В любом вписанном четырехугольнике сумма противоположных углов равна  .
.

Если сумма противоположных углов четырехугольника равна  , то около него можно описать окружность.
, то около него можно описать окружность.

Перпендикуляры, восстановленные к серединам сторон треугольника (серединные перпендикуляры) пересекаются в одной точке, которая является центром описанной окружности, и называется ортоцентром.
Оглавление
Многоугольники. 2
Параллелограмм и трапеция. 6
Прямоугольник, ромб, квадрат. 9
Площадь многоугольника. 13
Площади параллелограмма, треугольника и трапеции. 14
Теорема Пифагора. 16
Определение подобных треугольников. 18
Признаки подобия треугольников. 20
Применение подобия к доказательству теорем и решению задач. 22
Соотношения между сторонами и углами прямоугольного треугольника. 24
Касательная к окружности. 26
Центральные и вписанные углы.. 28
Четыре замечательные точки треугольника. 30
Вписанная и описанная окружности. 33