КУРСОВАЯ РАБОТА
Выполнила:
студентка 3 курса очной формы обучения
Блинкова Наталья Михайловна
Руководитель:
дфмн, проф. Хэкало С.П..
Итоговая оценка - ______________
Подпись______________________
Коломна – 2017 г.
Оглавление
1. Вступление…………………………………………………………………………3.
2. Инварианты (определение)………………………………………………………..4.
3. Виды матричных инвариантов
3.1.Определитель………………………………………………………………….....4.
3.2. Ранг матрицы……………………………………………………………………8.
3.3. След матрицы………………………………………………………………......10.
4. Применение матричных инвариантов для решения различных математических задач………………………………………………………………………………...12.
5. Заключение………………………………………………………………………13.
6. Литература……………………………………………………………………….14.
Вступление
Инварианты действий алгебраических групп изучаются достаточно давно. Начало теории инвариантов можно отнести к 50-м годам 19-го века, к работам Буля, Кэли, Эрмита и Сильвестра. В своих эпохальных работах Д.Гильберт (1893) доказал конечную порождаемость алгебры инвариантов линейно редуктивной группы. Новое развитие теория инвариантов получила в работах И. Шура, Г. Вейля, Р. Брауэра. Итог этой деятельности содержится в классической книге Г. Вейля (1947), посвященной инвариантом векторов и ковекторов классических линейных групп.
Естественным обобщением данной конструкции являются инварианты нескольких матриц под действием классической линейной группы диагонально сопряжениями. Матричные инварианты тесно связаны с такими разделами алгебры как теория представлений и теория алгебр с полиноминальными тождествами.
Более подробное рассмотрение матричных инвариантов изложено в данной курсовой работе.
Инвариант — это свойство некоторого класса (множества) математических объектов, остающееся неизменным при преобразованиях определённого типа.
В частности, существуют матричные инварианты, это характеристики матриц размерности 
, принадлежащих классу подобных, то есть задающих один и тот же линейный оператор 
, которые сохраняются неизменными на всем классе подобных представлений.
А также существуют матричные инварианты, это характеристики матриц размерности , принадлежащих классу подобных, то есть задающих один и тот же линейный оператор , которые для каждой реализации подобной матрицы оказываются своими.
Пусть {\displaystyle A} 
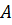- множество и 
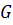- множество отображений из A в A. Отображение 
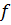из множества A в множество B называется инвариантом для G, если для любых 
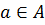{\displaystyle a\in A} и 
{\displaystyle g\in G}выполняется тождество 
.
Концепция инварианта является одной из важнейших в математике, поскольку изучение инварианта непосредственно связано с задачами классификации объектов того или иного типа. По существу, целью всякой математической классификации является построение некоторой полной системы инвариантов (по возможности, наиболее простой), то есть такой системы, которая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности.{\displaystyle f(a)=f(g(a))} ..ю
Инварианты используются в различных областях математики, таких как геометрия, топология и алгебра. Открытие инвариантов является важным шагом в процессе классификации математических объектов.
Виды матричных инвариантов
Определитель
Определитель (или детерминант) — одно из основных понятий линейной алгебры. Определитель квадратной матрицы 
{\displaystyle A} размеров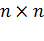 
{\displaystyle n\times n} 
заданной над коммутативным кольцом {\displaystyle R} 
является элементом кольца 
{\displaystyle R}, вычисляемым по формуле, приведённой ниже.
Он «определяет» свойства матрицы {\displaystyle A} 
. В частности, матрица {\displaystyle A} обратима тогда и только тогда, когда её определитель является обратимым элементом кольца {\displaystyle R} 
.
В случае, когда {\displaystyle R} — поле, определитель матрицы {\displaystyle A} равен нулю тогда и только тогда, когда ранг матрицы {\displaystyle A} меньше {\displaystyle n} 
или когда системы строк и столбцов матрицы {\displaystyle A} являются линейно зависимыми.
Определитель матрицы А обозначается как {\displaystyle \det(A)} 
, {\displaystyle |A|} 
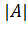или {\displaystyle \Delta (A)} 
.
Определения
Через перестановки
Для квадратной матрицы {\displaystyle A=(a_{ij})}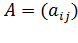 
размера {\displaystyle n\times n} 
её определитель {\displaystyle \det A} 
вычисляется по формуле:
{\displaystyle \det A=\sum _{\alpha _{1},\alpha _{2},\ldots,\alpha _{n}}(-1)^{N(\alpha _{1},\alpha _{2},\ldots,\alpha _{n})}\cdot a_{1\alpha _{1}}a_{2\alpha _{2}}\dots a_{n\alpha _{n}}} 
,
где суммирование проводится по всем перестановкам {\displaystyle \alpha _{1},\alpha _{2},\ldots,\alpha _{n}} 
чисел {\displaystyle 1,2,\dots,n}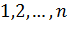 
а {\displaystyle N(\alpha _{1},\alpha _{2},\ldots,\alpha _{n})} 
обозначает число инверсий в перестановке {\displaystyle \alpha _{1},\alpha _{2},\ldots,\alpha _{n}} 
.
Таким образом, в определитель входит {\displaystyle n!}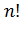 
слагаемых, которые также называют «членами определителя».
Эквивалентная формула:
{\displaystyle \det A=\sum _{i_{1},i_{2},\ldots,i_{n}=1}^{n}\varepsilon _{i_{1}i_{2}\dots i_{n}}\cdot a_{1i_{1}}a_{2i_{2}}\dots a_{ni_{n}}} 
,
где коэффициент {\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}} 
равен:
0, если не все индексы {\displaystyle i_{1},i_{2},\ldots,i_{n}} 
различны,
1, если все индексы {\displaystyle i_{1},i_{2},\ldots,i_{n}} различны и подстановка 
{\displaystyle {\begin{pmatrix}1&2&\dots &n\\i_{1}&i_{2}&\dots &i_{n}\end{pmatrix}}\in S_{n}} чётна, −1, если все индексы {\displaystyle i_{1},i_{2},\ldots,i_{n}} различны и подстановка {\displaystyle {\begin{pmatrix}1&2&\dots &n\\i_{1}&i_{2}&\dots &i_{n}\end{pmatrix}}\in S_{n}} нечётна.
Аксиоматическое построение (определение на основе свойств)
Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция 
{\displaystyle \det:\mathbb {R} ^{n\times n}\rightarrow \mathbb {R} } , обладающая следующими тремя свойствами:
1. {\displaystyle \det(A)} 
— кососимметрическая функция строк (столбцов) матрицы {\displaystyle A} 
.
2. {\displaystyle \det(A)} — полилинейная функция строк (столбцов) матрицы {\displaystyle A} .
3. {\displaystyle \det(E)=1} 
, где {\displaystyle E} 
— единичная {\displaystyle n\times n} 
-матрица.
Для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы.
{\displaystyle \Delta ={\begin{vmatrix}a_{11}\end{vmatrix}}=a_{11}}
Матрицы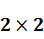 
Площадь параллелограмма равна модулю определителя матрицы, образованной векторами - сторонами параллелограмма.
Для матрицы {\displaystyle 2\times 2} 
определитель вычисляется как:
{\displaystyle \Delta ={\begin{vmatrix}a&c\\b&d\end{vmatrix}}=ad-bc}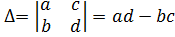 
Эта матрица может быть рассмотрена как матрица линейного отображения, преобразующего единичный квадрат в параллелограмм с вершинами 
.
Абсолютное значение определителя {\displaystyle |ad-bc|}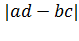 
равно площади этого параллелограмма, и, таким образом, отражает коэффициент, на который масштабируются площади при преобразовании A.
Значение определителя со знаком (ориентированная площадь параллелограмма) помимо коэффициента масштабирования также показывает, выполняет ли преобразование A отражение.
Матрицы 3 x 3
Определитель матрицы {\displaystyle 3\times 3} 
можно вычислить по формуле:
{\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=a_{11}{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}-a_{12}{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}+a_{13}{\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}=}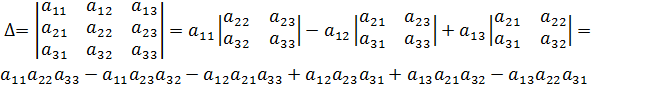 
{\displaystyle =a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}}
Для более удобного вычисления определителя третьего порядка можно воспользоваться правилом треугольника.
Определитель матрицы, составленной из векторов {\displaystyle \mathbf {a},\mathbf {b},\mathbf {c} } 
равен их смешанному произведению в правой декартовой системе координат. Аналогично двумерному случаю, определитель такой матрицы равен ориентированному объёму параллелепипеда, натянутого на {\displaystyle \mathbf {a},\mathbf {b},\mathbf {c} } .
Матрицы 
{\displaystyle N\times N}
В общем случае, для матриц более высоких порядков (выше 2-го порядка) {\displaystyle n\times n} определитель можно вычислить, применив следующую рекурсивную формулу:
{\displaystyle \Delta =\sum _{j=1}^{n}(-1)^{1+j}a_{1j}{\bar {M}}_{j}^{1}} 
, где {\displaystyle {\bar {M}}_{j}^{1}}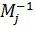 
— дополнительный минор к элементу {\displaystyle a_{1j}} 
. Эта формула называется разложением по строке.
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
{\displaystyle \Delta =\sum _{i=1}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}}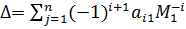 
Также справедливо и аналогичное разложение по любой строке (столбцу):
{\displaystyle \Delta =\sum _{j=1}^{n}(-1)^{i+j}a_{ij}{\bar {M}}_{j}^{ 
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым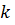 
строкам (столбцам):
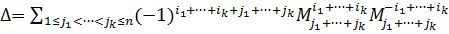{\displaystyle \Delta =\sum _{1\leqslant j_{1}<\ldots <j_{k}\leqslant n}(-1)^{i_{1}+\ldots +i_{k}+j_{1}+\ldots +j_{k}}M_{j_{1}\ldots j_{k}}^{i_{1}\ldots i_{k}}{\bar {M}}_{j_{1}\ldots j_{k}}^{i_{1}\ldots i_{k}}}
Основные свойства определителей:
Следующие свойства отражают основные результаты теории определителей, применение которых выходит далеко за пределы этой теории:
1. {\displaystyle \det E=1} 
(Определитель единичной матрицы равен 1);
2. {\displaystyle \det cA=c^{n}\det A} 
(Определитель является однородной функцией степени {\displaystyle n}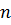 
на пространстве матриц размера {\displaystyle n\times n} 
);
3. {\displaystyle \det A^{T}=\det A}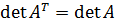 
(Определитель матрицы не меняется при её транспонировании);
4. {\displaystyle \det(AB)=\det A\cdot \det B} 
(Определитель произведения матриц равен произведению их определителей, A и B - квадратные матрицы одного и того же порядка);
5. {\displaystyle \det A^{-1}=(\det A)^{-1}}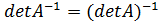 
, причём матрица {\displaystyle A} обратима тогда и только тогда, когда обратим её определитель {\displaystyle \det A}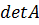 
;
6. Существует ненулевое решение уравнения {\displaystyle AX=0}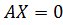 
тогда и только тогда, когда {\displaystyle \det A=0} 
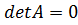(или же {\displaystyle \det A} 
должен быть нетривиальным делителем нуля в случае, если {\displaystyle R} 
- не целостное кольцо).
Ранг матрицы
Рангом системы строк (столбцов) матрицы {\displaystyle A} с {\displaystyle m} 
строк и {\displaystyle n} столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера ноль. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д.
Ранг матрицы — размерность образа {\displaystyle \dim(\operatorname {im} (A))}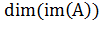 
линейного оператора, которому соответствует матрица.
Обычно ранг матрицы {\displaystyle A} обозначается {\displaystyle \operatorname {rang} A} 
, {\displaystyle \operatorname {rg} A}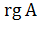 
или {\displaystyle \operatorname {rank} A} 
. Последний вариант свойственен для английского языка, в то время как первые два — для немецкого, французского и ряда других языков.
Определение
Пусть {\displaystyle A_{m\times n}} 
— прямоугольная матрица.
Тогда по определению рангом матрицы {\displaystyle A} является:
· ноль, если {\displaystyle A} — нулевая матрица;
· число {\displaystyle r\in \mathbb {N}:\;\exists M_{r}\neq 0,\;\forall M_{r+1}=0}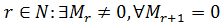 
, где {\displaystyle M_{r}} 
— минор матрицы {\displaystyle A} 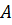порядка {\displaystyle r} 
, а {\displaystyle M_{r+1}} 
— окаймляющий к нему минор порядка {\displaystyle (r+1)} 
, если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы {\displaystyle A_{m\times n}}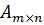 
порядка {\displaystyle k} 
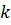равны нулю ({\displaystyle M_{k}=0} 
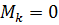). Тогда {\displaystyle \forall M_{k+1}=0} 
, если они существуют.
Связанные определения
· Ранг матрицы {\displaystyle A} размера {\displaystyle m\times n}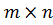 
называют полным, если {\displaystyle \operatorname {rang} A=\min\{m,n\}} 
.
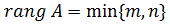· Базисный минор матрицы {\displaystyle A} — любой ненулевой минор матрицы {\displaystyle A} порядка {\displaystyle r}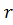 
, где {\displaystyle r=\operatorname {rang} A} 
.
· Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)
Свойства
· Теорема (о базисном миноре): Пусть {\displaystyle r=\operatorname {rang} A,M_{r}} 
— базисный минор матрицы {\displaystyle A} 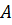, тогда:
1. базисные строки и базисные столбцы линейно независимые;
2. любая строка (столбец) матрицы {\displaystyle A} 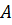есть линейная комбинация базисных строк (столбцов).
· Следствия:
· Если ранг матрицы равен {\displaystyle r} , то любые {\displaystyle p\colon p>r} 
строк или столбцов этой матрицы будут линейно зависимы.
· Если {\displaystyle A} 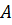— квадратная матрица, и {\displaystyle \det A=0} 
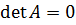, то строки и столбцы этой матрицы линейно зависимы.
· Пусть {\displaystyle r=\operatorname {rang} A} 
, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно {\displaystyle r} .
Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение {\displaystyle A\sim B} 
для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если {\displaystyle A\sim B} 
, то их ранги равны.
Теорема Кронекера — Капелли: Системa линейных алгебраических уравнений совместна тoгда и тoлько тoгда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
· Количество главных переменных системы равно рангу системы.
· Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Неравенство Сильвестра:
Если A и B матрицы размеров 
и 
, то {\displaystyle \operatorname {rang} AB\geq \operatorname {rang} A+\operatorname {rang} B-n} 