3.1. Ферма Пьер, один из создателей аналитической геометрии и дифференциального исчисления. Открыл правило нахождения экстремума с помощью производной.
Теорема Ферма (Пьер Ферма (1601-1665) – французский математик). Если функция  , определенная в интервале
, определенная в интервале 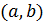 , достигает в некоторой точке
, достигает в некоторой точке  этого интервала наибольшего (или наименьшего) значения и существует производная
этого интервала наибольшего (или наименьшего) значения и существует производная 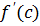 , то
, то 
Доказательство. Допустим, что в точке  функция
функция 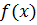 достигает наибольшего значения. Придадим значению
достигает наибольшего значения. Придадим значению  достаточно малое приращение
достаточно малое приращение  . Тогда
. Тогда 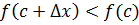 . Отсюда при
. Отсюда при 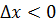
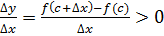 ,
,
и, следовательно,
 (1)
(1)
При 
 , и, следовательно,
, и, следовательно,
 (2)
(2)
Из неравенств (1) и (2) следует, что  . Что и требовалось доказать.
. Что и требовалось доказать.
Геометрический смысл заключения теоремы состоит в том, что касательная к графику функции  в точке с абсциссой
в точке с абсциссой 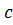 параллельна оси абсцисс.
параллельна оси абсцисс.
Замечание! Теорема Ферма дает только необходимый признак локального экстремума, но не достаточного, то есть дифференцируемая функция в точке экстремума обязана иметь производную равную нулю. Из того, что в какой-то точке производная равна нулю не следует, что эта точка является локальным экстремумом. Для того, чтобы в этом убедиться рассмотрим простейший пример.
Пример. Пусть  , тогда
, тогда 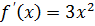 . Из этого следует, что
. Из этого следует, что  и
и  . Таким образом, в точке
. Таким образом, в точке 
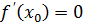 , но
, но 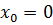 не является локальным экстремумом так как функция
не является локальным экстремумом так как функция 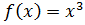 возрастает на всей числовой прямой R.
возрастает на всей числовой прямой R.
Пусть  , покажем, что
, покажем, что 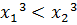 .
. 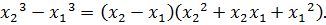 Очевидно, что
Очевидно, что  и
и  . Что и требовалось доказать.
. Что и требовалось доказать.
Таким образом, теорема Ферма позволяет лишь отсечь точки, подозрительные на экстремумы, сужая поиски.
3.2. Теорема Ролля (Мишель Ролль (1652-1719) – французский математик). Если функция  , непрерывная на отрезке
, непрерывная на отрезке 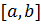 и дифференцируемая на интервале
и дифференцируемая на интервале 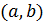 , принимает на концах этого отрезка равные значения
, принимает на концах этого отрезка равные значения 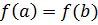 , то на интервале
, то на интервале 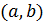 существует такая точка
существует такая точка  , что
, что  .
.
Доказательство. Так как функция 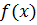 непрерывная на отрезке
непрерывная на отрезке 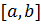 , то, как известно, она принимает на этом отрезке как свое наибольшее значение M, так и свое наименьшее значение m. Возможны только два случая.
, то, как известно, она принимает на этом отрезке как свое наибольшее значение M, так и свое наименьшее значение m. Возможны только два случая.
Случай первый. M=m. Тогда 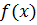 постоянна на отрезке
постоянна на отрезке 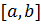 : в самом деле, неравенство
: в самом деле, неравенство  в этом случает дает
в этом случает дает  для всех x из отрезка
для всех x из отрезка 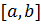 . Поэтому в любой точке интервала
. Поэтому в любой точке интервала 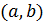

Случай второй. M>m. Так как  то хоть одно из значений M и m достигается в некоторой точке
то хоть одно из значений M и m достигается в некоторой точке  Следовательно, согласно теореме Ферма
Следовательно, согласно теореме Ферма  Теорема доказана.
Теорема доказана.
Геометрически теорема Ролля означает следующее: если крайние координаты кривой  равны, то на кривой найдется точка, где касательная параллельна оси абсцисс.
равны, то на кривой найдется точка, где касательная параллельна оси абсцисс.
Следствие.
Если  , то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
3.3. При изучении различных свойств функции особое место занимает теорема Лагранжа, благодаря этой теореме можно найти условия постоянства и монотонности функции. Также в теоремах Лагранжа доказываются достаточные условия экстремума.
Теорема Лагранжа (Жозеф-Луи Лагранж (1736-1813) - французский математик и механик). Если функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале  , то на интервале
, то на интервале  найдется такая точка
найдется такая точка  , что
, что  . (3)
. (3)
Доказательство. Положим  (4) и рассмотрим вспомогательную функцию
(4) и рассмотрим вспомогательную функцию 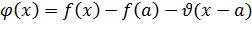 .Эта функция удовлетворяет первым двум условия теоремы Ролля как алгебраическая сумма трех непрерывных и дифференцируемых функций. При этом
.Эта функция удовлетворяет первым двум условия теоремы Ролля как алгебраическая сумма трех непрерывных и дифференцируемых функций. При этом 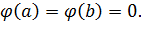 Следовательно, к функции
Следовательно, к функции  применима теорема Ролля, то есть существует точка
применима теорема Ролля, то есть существует точка 
 , такая, что
, такая, что  . Но
. Но 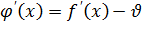 . Поэтому
. Поэтому  или
или 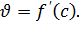 отсюда с учетом формулы (4) получаем искомое равенство (3).
отсюда с учетом формулы (4) получаем искомое равенство (3).
Теорема Лагранжа имеет простой геометрический смысл: на графике функции  между точками
между точками  и
и  есть внутренняя точка
есть внутренняя точка 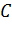 такая, что касательная к нему в точке
такая, что касательная к нему в точке 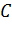 параллельная хорде
параллельная хорде  . В самом деле, левая часть равенства (3) - угловой коэффициент хорды, а правая - угловой коэффициент касательной к графику в точке
. В самом деле, левая часть равенства (3) - угловой коэффициент хорды, а правая - угловой коэффициент касательной к графику в точке 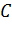 .
.
Примечание. Теорема Лагранжа является обобщением теоремы Ролля, так как если  то из равенства (3) следует
то из равенства (3) следует 
Формула (3) называется формулой Лагранжа или формулировкой конечных приращений. Из нее получаем 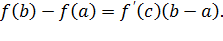 Наконец, взяв вместо
Наконец, взяв вместо  и
и 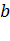 соответственно
соответственно  и
и 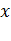 и обозначив
и обозначив  , формулу Лагранжа запишем
, формулу Лагранжа запишем 
Из теоремы Лагранжа вытекает следствие: Если  на интервале
на интервале  , то на этом интервале
, то на этом интервале  постоянна.
постоянна.
Доказательство. Для любых значений 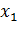 и
и  (
( из рассматриваемого интервала выполняется теорема Лагранжа, то есть
из рассматриваемого интервала выполняется теорема Лагранжа, то есть  где
где 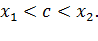 Но
Но  а потому и
а потому и  то есть
то есть  , а это означает, что
, а это означает, что 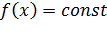 на интервале
на интервале  Что и требовалось доказать.
Что и требовалось доказать.
3.4. Теорема об интегральном среднем
Теорема об интегральном среднем является следствием из свойства о двойном интеграле, а именно: Если  интегрируемы на отрезке
интегрируемы на отрезке  и
и 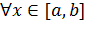
 то
то  . (1)
. (1)
Доказательство. Пусть  интегрируема на отрезке
интегрируема на отрезке  и ограничена на этом же отрезке. Обозначим
и ограничена на этом же отрезке. Обозначим  и
и  ,
,  .
.
Так как  интегрируема на любом отрезке, то можно рассмотреть 3 функции:
интегрируема на любом отрезке, то можно рассмотреть 3 функции: 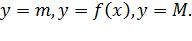 Все они интегрируемы на отрезке
Все они интегрируемы на отрезке  .
.
Тогда в силу свойства (1) получим следующую цепочку неравенств по отрезку  :
:
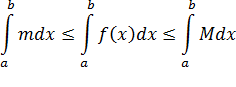


Число 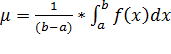 называется интегральным среднем.
называется интегральным среднем.
Особый интерес представляет случай, когда функция  непрерывна на отрезке
непрерывна на отрезке  .
.
Пусть  непрерывна на отрезке
непрерывна на отрезке  , тогда по теореме о промежуточных значениях функции заключаем, что
, тогда по теореме о промежуточных значениях функции заключаем, что  Тогда
Тогда  .
.
Геометрический смысл полученного равенства. Полученное равенство означает, что интеграл по отрезку от непрерывной функции можно заменить интегралом от некоторой константы по тому же отрезку.
Геометрически это означает, что мы можем заменить площадь криволинейной трапеции площадью некоторого прямоугольника, основание которого совпадает с отрезком  .
.
В общем случаем мы получаем, что 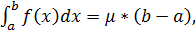 где
где 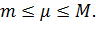 Что и требовалось доказать.
Что и требовалось доказать.
3.5. Теорема о существовании точных верхней и нижней граней у ограниченного множества
Любое ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.
Доказательство. Пусть  ограниченное сверху непустое числовое множество. Обозначим через
ограниченное сверху непустое числовое множество. Обозначим через  множество всех чисел, ограничивающих сверху множество
множество всех чисел, ограничивающих сверху множество  Множество
Множество  ограничено сверху, поэтому множество
ограничено сверху, поэтому множество  не пусто. Каждый элемент
не пусто. Каждый элемент 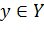 ограничивает сверху множество
ограничивает сверху множество 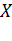 , то есть
, то есть 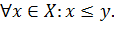 Элементы
Элементы 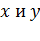 являются произвольными элементами соответственно множеств
являются произвольными элементами соответственно множеств  поэтому, в силу свойства непрерывности действительных чисел,
поэтому, в силу свойства непрерывности действительных чисел, 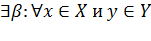 имеет место неравенство
имеет место неравенство 
Выполнение неравенства  означает, что число
означает, что число  ограничивает сверху множество
ограничивает сверху множество 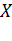 , а выполнение неравенства
, а выполнение неравенства  для всех
для всех 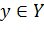 , то есть для всех чисел, ограничивающих сверху множество
, то есть для всех чисел, ограничивающих сверху множество 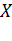 , означает, что число
, означает, что число  является наименьшим среди всех таких чисел, то есть верхней гранью множества
является наименьшим среди всех таких чисел, то есть верхней гранью множества 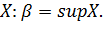
Существование верхней грани у ограниченного сверху непустого множества доказано.
Если теперь непустое ограниченное снизу числовое множество, то отнесем к множеству 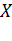 все числа, ограничивающие снизу множество
все числа, ограничивающие снизу множество 
Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства непрерывности действительных чисел  имеет место неравенство
имеет место неравенство 
Это означает, что 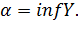 Теорема доказана.
Теорема доказана.