Дадим определение однородной функции нескольких переменных: функция нескольких переменных называется однородной функцией этих переменных степени m, если при умножении этих переменных на произвольную величину t функция умножается на tm , т.е. имеет место тождество
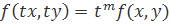или 
(1)
при любых допустимых значениях переменных x, y, z, t. Число m может быть любым фиксированным вещественным числом. Если, например, m= 
, то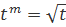 
и t должны быть положительными. Положим, что функция f(x,y), выражает некоторый объем, что x и y это длины некоторых линий и что в выражении f(x,y), кроме этих линий, входят отвлеченные числа. Умножение x и y на t (положительное число) равносильно уменьшению линейного масштаба в t раз (при t>1 или увеличению при t<1), и, очевидно, что при этом функция f(x,y), выражающая объем, должна умножаться на t3 , т.е. рассматриваемом случае функция f(x,y) будет однородной функцией третьей степени. Так, например, объем конуса выражается через радиус его основания x и высоту y по формуле 
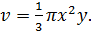Эта функция будет однородной третьей степени при всех вещественных x, y, и t. Такой же функцией будет и любой однородный многочлен от x и y третьей степени, т.е. такой многочлен, в каждом члене которого сумма показателей x и y равна трем:
.
Дроби
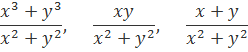
это однородные функции степеней соответственно 1, 0 и (-1).
Отметим, что f(x,y)=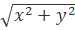 
, где радикал считается арифметическим, будет однородной функцией первой степени при всех вещественных x и y и при всех t>0. Действительно,
причем оба радикала считаются положительными.
Дифференцируя тождество (1) по t и применяя правило дифференцирования сложной функции, получим, полагая 
:
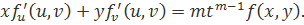
Полагая 
, находим
(2)
что выражает следующую теорему Эйлера. об однородных функциях:
Сумма произведений частных производных однородной функции на соответствующие переменные равна произведению самой этой функции на степень ее однородности.
При доказательстве мы считаем естественно, что функция f(x, y) имеет непрерывные частные производные при соответствующих значениях переменных, которыми мы пользовались при доказательстве.
Если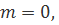 
то, положив в тождестве (1) 
, мы получим
или 
т.е. однородная функция нулевой степени есть функция отношения всех переменных, кроме одной, к этой последней переменной. Часто однородную функцию нулевого измерения называют просто однородной.
Примеры использования однородных функций в дифференциальных уравнениях 1-ого порядка
В данном параграфе мы рассмотрим так называемые однородные дифференциальные уравнения первого порядка. Наряду с уравнениями с разделяющимися переменными линейными неоднородными уравнениями этот тип ДУ[3] встречается практически в любой контрольной работе по теме диффуров.
В чём отличие однородных дифференциальных уравнений от других типов ДУ? Это проще всего сразу же пояснить на конкретном примере.
Пример.
Решить дифференциальное уравнение 
Решение:
Что в первую очередь следует проанализировать при решении любого дифференциального уравнения первого порядка? В первую очередь необходимо проверить, а нельзя ли сразу разделить переменные с помощью «школьных» действий? Обычно такой анализ проводят мысленно или пытаются разделить переменные на черновике.
В данном примере переменные разделить нельзя (можете попробовать перекидывать слагаемые из части в часть, выносить множители за скобки и т.д.). Кстати, в данном примере, тот факт, что переменные разделить нельзя, достаточно очевиден ввиду наличия множителя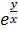 
Возникает вопрос – как же решить это дифференциальное уравнение?
Нужно проверить, а не является ли данное уравнение однородным? Проверка несложная, и сам алгоритм проверки можно сформулировать так:
В исходное уравнение:
вместо x подставляем 
, вместо y подставляем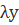 
, производную не м
трогаем:
Буква лямбда – это условный параметр, и здесь он играет следующую роль: если в результате преобразований удастся «уничтожить» ВСЕ лямбды и получить исходное уравнение, то данное дифференциальное уравнение является однородным.
Очевидно, что лямбды сразу сокращаются в показателе степени:
Теперь в правой части выносим лямбду за скобки:
и обе части делим на эту самую лямбду:
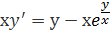В результате, все лямбды исчезли, и мы получили исходное уравнение.
Вывод: Данное уравнение является однородным
Как решить однородное дифференциальное уравнение?
Абсолютно все однородные уравнения можно решить с помощью одной-единственной (!) стандартной замены.
Функцию «игрек» следует заменить произведением некоторой функции t (тоже зависящей от «икс») и «икса»:
y=t(x) 
x, почти всегда пишут коротко: y=tx
Выясняем, во что превратится производная 
при такой замене, используем правило дифференцирования произведения. Если y=tx, то: 
Подставляем y=tx и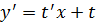 
в исходное уравнение 
: 
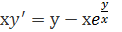Что даст такая замена? После данной замены и проведенных упрощений мы гарантировано получим уравнение с разделяющимися переменными. Запоминаем: y= 
и, соответственно, 
.
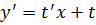После подстановки проводим максимальные упрощения:
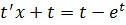
Далее алгоритм работает по накатанной колее уравнения с разделяющимися переменными.
Поскольку t – это функция, зависящая от «икс», то её производную можно записать стандартной дробью: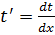 
.
Таким образом: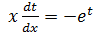 
Разделяем переменные, при этом в левой части нужно собрать только «тэ», а в правой части – только «иксы»:
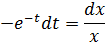Переменные разделены, интегрируем:
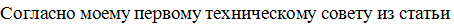Дифференциальные уравнения первого порядка константу во многих случаях целесообразно «оформить» в виде логарифма.
После того, как уравнение проинтегрировано, нужно провести обратную замену, она тоже стандартна и единственна:
Если y= , то 
В данном случае: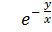 
= 
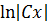
Ответ: общий интеграл: =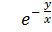 
, где C=const