Устойчивость линейных систем автоматического регулирования
Наиболее важными динамическими свойствами системы являются: устойчивость, время регулирования, время перерегулирования, число колебаний регулируемой величины.
Основная характеристика: устойчивость, т.к. три последних требования могут измениться в зависимости от назначения и условий работы установки, а требования устойчивости должно удовлетворять САУ.
В зависимости от характера переходного процесса линеаризованной системы различают три основных случая поведения системы после возмущающего воздействия:
1) система не может восстановить равновесное состояние, значения управляемой переменной (выходной величины) все больше откланяется от заданного, такой процесс называется расходящимся, а система неустойчивой;
2) Система возвращается в равновесное состояние значение управляемой переменной отличается от заданного на величину статической ошибки, такой процесс называется сходящимся, а система устойчивой;
3) Система характеризуется установившимся периодическим движением, такой процесс называется колебательным, а система будет находиться на границе асимптотической устойчивости.
Математическое условие устойчивости систем управления.
По графику переходного процесса можно однозначно провести оценку устойчивости системы: необходимо найти выходной сигнал системы, который определяется из дифференциального уравнения САУ:
Решение данного уравнения дает нам слагаемые
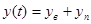
Ув – вынужденная составляющая выходного сигнала.
Уп – переходная составляющая выходного сигнала.
При чем Уп определяет поведение системы после снятия нагрузки (или сил), следовательно, зная Уп можно определить устойчивость системы, при этом Уп полностью определяется полиномом D(p), который равен:
а этот полином определяет вид знаменателя передаточной функции (по нему можно определить устойчивость системы). Решение данного полинома в общем виде:
, где s1–sn – корни данного полинома, они же корни характеристики этого уравнения, т.е. корни знаменателя передаточной функции С1-Cn – постоянные интегрирования.
Допустим, что у нас уравнение первого порядка, при чем корень вещественный, возможно, что отрицательный или положительный.
Если система II-го порядка, то в ней возможно появление комплексных сопряженных корней (возможны три случая):
а) корни содержат отрицательную вещественную часть В этом случае график представляет собой затухающие колебания (т.е. устойчивая система);
б) если корень с положительной вещественной частью, то получим расходящиеся колебания, т.е. система неустойчивая;
в) корни имеют нулевую вещественную часть (получим затухающие колебания), т.е. безразличную систему (система находится на границе устойчивости)
Для систем любого порядка, в которых корни могут быть комбинацией предыдущих случаев - оказывается, что даже одна положительная вещественная часть какого-либо корня приводит к неустойчивому переходному процессу.
Для устойчивости системы необходимо и достаточно, чтобы вещественная часть всех корней характеристического уравнения была отрицательна, если имеется хотя бы один корень с положительной вещественной частью, то система неустойчива.
Если в системе имеется хотя бы один нулевой корень (s = 0), то система находится на апериодической границе устойчивости.
Если есть хотя бы одна пара чисто мнимых корней, т.е. 
(α = 0), то система находится на колебательной границе устойчивости. Для таких систем ничего нельзя сказать об устойчивости, поскольку математическая модель и математическое описание для линейных систем имеет ряд упрощений и допущений.
Т.к. нахождение корней характеристического уравнения высокого порядка является затруднительным (все математические пакеты позволяют найти корни только приблизительными методами, следовательно не обладают 100% точностью) поэтому были разработаны специальные критерии оценки устойчивости, без нахождения корней.