Цель – повторить свойства функции, нули функции, промежутки монотонности, интервалы знакопостоянсва, область определение и область значения, формулу разложения квадратного трехчлена на множители. Рассмотреть это на конкретных задачах.
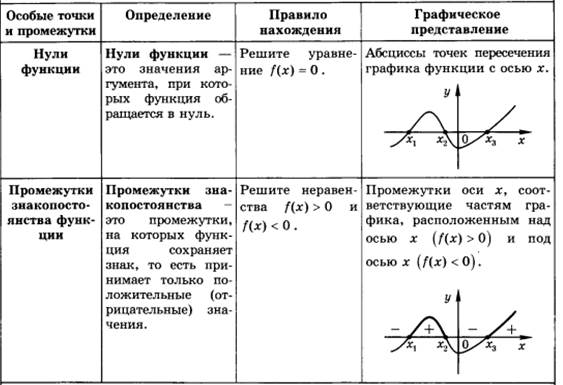
Рассмотрим нахождение данных элементов на примере
Выделение квадрата двучлена
Как выделить полный квадрат двучлена в квадратном трёхчлене?
Начнём, разумеется, с простого.
Уровень 1. Коэффициент при x2 равен 1
Это самая простая ситуация, требующая минимум дополнительных преобразований.
Например, дан квадратный трёхчлен:
х2+4х+6
Внешне выражение очень похоже на квадрат суммы. Мы знаем, что в квадрате суммы сидят чистые квадраты первого и второго выражений (a2 и b2), а также удвоенное произведение 2ab этих самых выражений.
Ну, квадрат первого выражения у нас уже присутствует в чистом виде. Это х2. Собственно, именно в этом и заключается простота примеров этого уровня. Нужно получить квадрат второго выражения b2. Т.е. найти b. И зацепкой будет служить выражение с иксом в первой степени, т.е. 4х. Ведь 4х можно представить в виде удвоенного произведения икса на двойку. Вот так:
4x = 2́·х·2
Значит, если 2ab=2·x·2 и a=x, то b=2. Можно записать:
х2+4х+6 = х2+2́·х·2+22….
Так нам хочется. Но! Математике хочется, чтобы от наших действий суть исходного выражения не изменилась. Так уж она устроена. Мы прибавили к удвоенному произведению 22, тем самым изменив исходное выражение. Значит, чтобы математику не обидеть, это самое 22 надо тут же и отнять. Вот так:
…= х2+2́·х·2+ 22 - 22 ….
Почти всё. Остаётся лишь добавить 6, в соответствии с исходным трёхчленом. Шестёрка-то никуда не делась! Пишем:
= х2+2́·х·2+22- 22+6 = …
Теперь первые три слагаемых дают чистый (или — полный) квадрат двучлена x+2. Или (x+2)2. Чего мы и добиваемся.) Я даже не поленюсь и скобочки поставлю:
… = (х2+2́·х·2+22) - 22+6 =…
Скобки сути выражения не меняют, зато чётко подсказывают, что, как и почему. Осталось свернуть эти три слагаемых в полный квадрат по формуле, сосчитать в числах оставшийся хвостик -22+6 (это будет 2) и записать:
х2+4х+6 = (x+2)2+2
Всё. Мы выделили квадрат скобок (x+2)2 из исходного квадратного трёхчлена х2+4х+6. Превратили его в сумму полного квадрата двучлена (x+2)2 и некоторого постоянного числа (двойки). А теперь я запишу всю цепочку наших преобразований в компактном виде. Для наглядности.
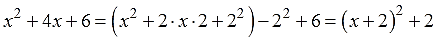
И все дела.) Вот и вся суть процедуры выделения полного квадрата.
Кстати, чему здесь равны числа m и n? Да. Каждое из них равно по двойке: m=2, n=2. Так уж получилось в ходе выделения.
Уровень 2. Коэффициент при x2 не равен 1 — как быть?
Это более общий случай по сравнению со случаем а=1. Объём вычислений, разумеется, возрастает. Это огорчает, да… Зато общий ход решения в целом остаётся прежним. Просто к нему добавляется всего один новый шаг. Это радует.)
Пока рассмотрим безобидный случай, безо всяких дробей и прочих подводных камней. Например:
2x2-4x+6
В серединке стоит минус. Значит, будем подгонять под квадрат разности. Но коэффициент при квадрате икса — двойка. А проще работать с единичкой. C чистым иксом. Что делать? А вынесем-ка эту двойку за скобки! Чтоб не мешала. Имеем право! Получим:
2(x2-2x+3)
Вот так. Теперь трёхчлен в скобках — уже с чистым иксом в квадрате! Как того требует алгоритм уровня 1. И теперь уже можно работать с этим новым трёхчленом по старой отработанной схеме. Вот и действуем. Выпишем-ка его отдельно да преобразуем:
x2-2x+3 = x2-2·x·1+12 -12+3 = (x2-2·x·1+12) -12+3 = (x-1)2+2
Полдела сделано. Осталось вставить полученное выражение внутрь скобок, да раскрыть их обратно. Получится:
2(x2-2x+3) = 2((x-1)2+2) = 2(x-1)2+4
Готово!
Ответ:
2x2-4x+6 = 2(x-1)2+4
А если коэффициенты b и с не делятся нацело на а? Это — самый общий и одновременно самый скверный случай. Тогда только дроби, да… Ничего не поделать. Например:
3x2+2x-5
Всё аналогично, отправляем тройку за скобки, получаем:
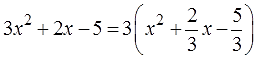
К сожалению, ни двойка, ни пятёрка нацело на тройку не делятся, поэтому коэффициенты нового (приведённого) трёхчлена — дробные. Ну и ничего страшного. Работаем прямо с дробями: две трети икс превращаем в удвоенное произведение икса на одну треть, прибавляем квадрат одной трети (т.е. 1/9), отнимаем его, отнимаем 5/3…
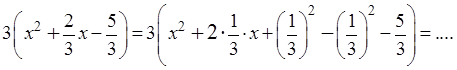
В общем, вы поняли!
Дорешайте, чего уж там. Должно в итоге получиться:
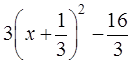
И ещё одни грабли. Многие ученики лихо расправляются с положительными целыми и даже дробными коэффициентами, но зависают на отрицательных. Например:
-x2+2x-3
Что делать с минусом перед x2? В формуле квадрата суммы/разности всяко плюс нужен… Не вопрос! Всё то же самое. Выносим этот самый минус за скобки. Т.е. минус единицу. Вот так:
-x2+2x-3 = -(x2-2x+3) = (-1)·(x2-2x+3)
И все дела. А с трёхчленом в скобках - опять по накатанной колее.
x2-2x+3 = (x2-2x+1) -1+3 = (x-1)2+2
Итого, с учётом минуса:
-x2+2x-3 = -((x-1)2+2) = -(x-1)2-2
Найти наименьшее значение квадратного трехчлена.
Чтоы найти наименьшее или наибольшее значени квадратного трехчлена, в нем нужно выделить квадрат двучлена.
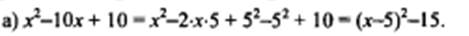
Наименьшее значение равно -15, при x-5=0, то есть x=5
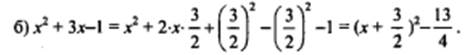
Наименьшее значение равно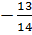 
, при x+ 
=0, то есть при x=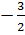 
Если возле x2 стоит знак минус, его нужно вынести за скобку и знаки в скобках поменять на противоположные и выделить квадрат двучлена. Тогда функция будет принимать наибольше значение.
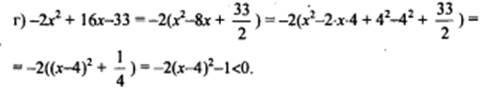
Наибольшее значение равно -1, при x-4 равно 0, то есть при x=4.
Все изучить, разобрать, следующий урок контрольная работа.
