Парабола и её каноническое уравнение

Парабола и её каноническое уравнение

Каноническое уравнение параболы имеет вид 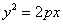, где 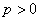– действительное число. Нетрудно заметить, что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция 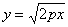задаёт верхнюю ветвь данной линии, а функция 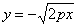– нижнюю ветвь. Очевидно, что парабола симметрична относительно оси .

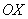Пример 1

Построить параболу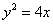

Решение: вершина известна, найдём дополнительные точки. Уравнение 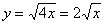определяет верхнюю дугу параболы, уравнение 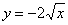– нижнюю дугу.

Проведем вычисления: :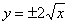

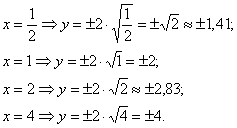
Перед построением чертежа повторим определение параболы:

Параболой называется множество всех точек плоскости, равноудалённых от данной точки 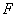и данной прямой 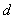, не проходящей через точку .

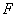Точка 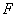называется фокусом параболы, прямая 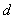– директрисой параболы. Константа «пэ» канонического уравнения 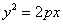называется фокальным параметром, который равен расстоянию от фокуса до директрисы. В данном случае 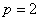. При этом фокус имеет координаты 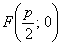, а директриса задаётся уравнением .
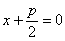В нашем примере :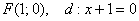

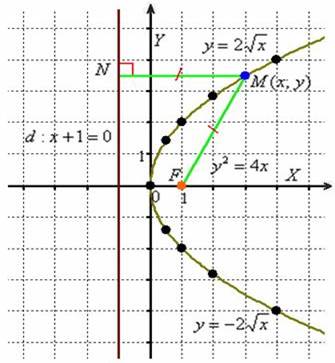
Определение параболы понимается ещё проще, чем определения эллипса и гиперболы. Для любой точки 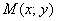параболы длина отрезка 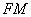(расстояние от фокуса до точки) равна длине перпендикуляра 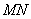(расстоянию от точки до директрисы):

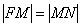
При увеличении фокального параметра ветви графика 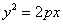будут «раздаваться» вверх и вниз, бесконечно близко приближаясь к оси 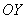. При уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси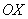

Эксцентриситет любой параболы равен единице: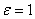

Пример 2

Построить параболу 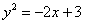. Привести уравнение линии к каноническому виду, найти фокус и уравнение директрисы.

Решение: преобразуем уравнение: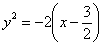
Вершина параболы находится в точке 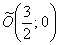, ветви направлены влево. С помощью уравнений 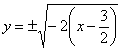найдём дополнительные точки:

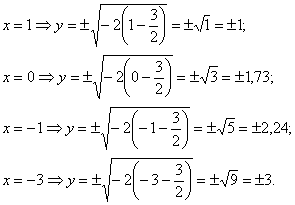
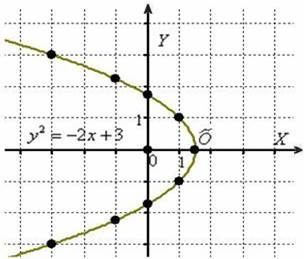
Выполним чертёж:

Парабола 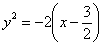получена путём поворота параболы 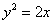на 180 градусов и её параллельного переноса в точку 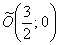. Из канонического уравнения 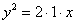находим фокальный параметр 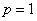, фокус 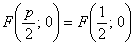и уравнение директрисы .

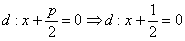По условию требуется построить параболу 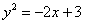. Именно такую – в неканоническом виде! Поэтому в первой части задачи следует представить уравнение в виде 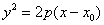, что позволит сразу определить вершину. Затем по образцу Примера 6 нужно провести поточечное построение линии, работая с уравнениями .

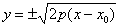Пример 3.

Зная расположение фокусной точки, составить каноническое уравнение параболы. Координаты точки фокуса F (4;0).

Решение: Каноническое уравнение параболы имеет вид .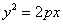
Так как мы рассматриваем параболу, график которой задан каноническим уравнением, следовательно, расстояние от фокуса до вершины равно 0,5 фокального параметра 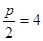, тогда p=8. Подставим значение p в каноническую форму уравнения, наше уравнение примет вид y²=16x.

Пример 4. Определить координаты фокуса параболы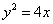

Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае - в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:

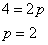
Находим координаты фокуса параболы:

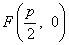
Пример 5. Составить уравнение директрисы параболы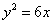

Решение. Находим p:

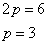
Получаем уравнение директрисы параболы:

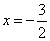
Пример 6.

Составить каноническое уравнение параболы, если точка (5;-5) принадлежит параболе.

Решение. Каноническое уравнение параболы имеет вид 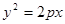. Подставим в него координаты заданной точки (5;-5):

(-5)²=2p*5

откуда 2p=5.

Тогда искомое уравнение параболы будет иметь вид

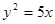
Ответ Каноническое уравнение параболы имеет вид: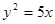

Пример 7.

Парабола y ² = 2 px проходит через точку A (2, 4). Определить ее параметр p.

Решение. Подставляем в уравнение параболы вместо текущих координат координаты точки A (2, 4). Получаем

4² = 2 p *2; 16 = 4 p; p = 4.

Задание для самостоятельной работы

Задание 1.

а) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у²=16р.

б) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

у²= -18р.

Задание 2.

а) Составить каноническое уравнение параболы и ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; -7).

б) Составить каноническое уравнение параболы и ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; 4).

Задание 3.

а) Парабола y ² = 2 px проходит через точку A (4; 8). Определить ее параметр p.

б) Парабола y ² = - 2 px проходит через точку A (-4; -8). Определить ее параметр p.