Объем  тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной кривой
тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной кривой  , прямыми
, прямыми  выражается интегралом
выражается интегралом

Объем 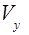 тела, образованный вращением вокруг оси ОУ криволинейной трапеции, ограниченной кривой
тела, образованный вращением вокруг оси ОУ криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми  определяется формулой
определяется формулой
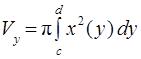 .
.
5.2(1). 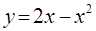 ,
,  ,
, 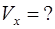
Решение .
На рис. 2 изображена область, ограниченная параболой 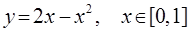 и прямой
и прямой  , на рис. 3 - тело, полученное вращением вокруг оси
, на рис. 3 - тело, полученное вращением вокруг оси  фигуры, изображенной на рис.2.
фигуры, изображенной на рис.2.


Рис. 2. Рис. 3.
Объем тела вращения вокруг оси  состоит из двух частей – тела, полученного вращением вокруг оси
состоит из двух частей – тела, полученного вращением вокруг оси  параболы
параболы 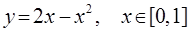 (параболоида вращения) и конуса - тела, полученного вращением вокруг оси ОХ прямой
(параболоида вращения) и конуса - тела, полученного вращением вокруг оси ОХ прямой  . Следовательно,
. Следовательно,

Ответ:  (куб. ед.).
(куб. ед.).
5.2(2). 
Решение .
На рис. 4 изображена область, ограниченная параболой  и прямыми линиями:
и прямыми линиями: 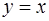 и
и  На рис. 5 изображено тело вращения вокруг оси
На рис. 5 изображено тело вращения вокруг оси 

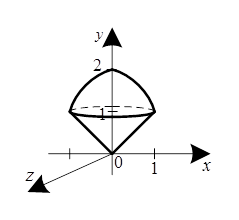
Рис. 4 Рис. 5.
Согласно правилу вычисления объемов вращения вокруг оси 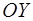 , получим
, получим

Ответ:  (куб. ед.).
(куб. ед.).
ДВОЙНОЙ ИНТЕГРАЛ.
Обобщением определенного интеграла на случай функции двух переменных  является двойной интеграл [2]:
является двойной интеграл [2]:
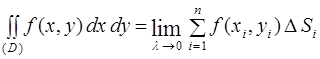 .
.
Область интегрирования  называется правильной, если прямые, проведенные через любую внутреннюю точку области
называется правильной, если прямые, проведенные через любую внутреннюю точку области  параллельно осям
параллельно осям  и
и 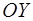 пересекают границу области
пересекают границу области  не более чем в двух точках. Двойной интеграл от непрерывной в правильной области
не более чем в двух точках. Двойной интеграл от непрерывной в правильной области  функции
функции  сводится к повторному интегралу [2], т.е. к последовательному вычислению двух определенных интегралов.
сводится к повторному интегралу [2], т.е. к последовательному вычислению двух определенных интегралов.
Задание 6. 6.1 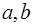 .Изменить порядок интегрирования в повторном интеграле; 6.2. Найти среднее значение функции
.Изменить порядок интегрирования в повторном интеграле; 6.2. Найти среднее значение функции  в области:
в области:  .
.
6.1.а. 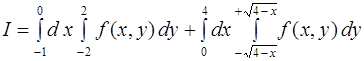 ,
,
6.1.b. 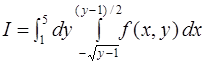 .
.
6.1. а. 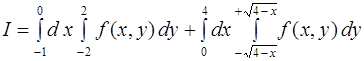 ,
,
Решение.
Опишем область интегрирования  .
.
Уравнение нижней границы:  если
если 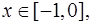 и
и  , т.е.
, т.е. 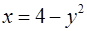 , если
, если 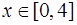 . Уравнение верхней границы области
. Уравнение верхней границы области  :
:
 если
если 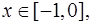 и
и  , т.е.
, т.е. 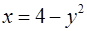 , если
, если 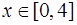 .
.
Область  изображена на рис.6. Область
изображена на рис.6. Область  правильная, ее можно
правильная, ее можно


Рис. 6 Рис. 7
описать и так (рис. 7): 
Согласно правилу расстановки пределов в повторных интегралах, получим
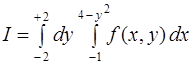 .
.
Ответ: 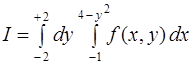 .
.
6. 1. b. 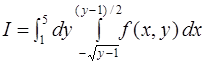 .
.
Решение. Область интегрирования  определяется соотношениями:
определяется соотношениями:

Кривая  левая ветвь параболы
левая ветвь параболы  (рис. 9).
(рис. 9).


Рис. 8 Рис. 9
Уравнение прямой 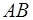 :
:  или
или 
Точки 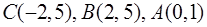 - это точки пересечения параболы
- это точки пересечения параболы  с прямыми
с прямыми  и
и 
Область  состоит из двух областей:
состоит из двух областей:  :
:  и
и  .
.
На рис. 8 указаны уравнения границ области, которые надо использовать для области, правильной в направлении оси 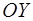 .
.
Следуя правилам составления повторного интеграла, получим
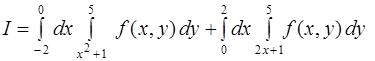
Ответ: 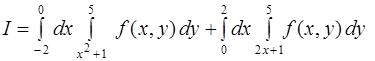
Средним значением функции 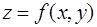 в области
в области  называется выражение
называется выражение
 .
.
Здесь  площадь области
площадь области  .
.
6.2. Найти среднее значение функции  в области:
в области:  .
.
Решение. Область интегрирования  - прямоугольник, изображена на рис. 10. Очевидно,
- прямоугольник, изображена на рис. 10. Очевидно, 
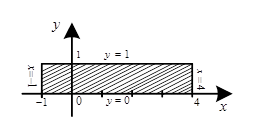
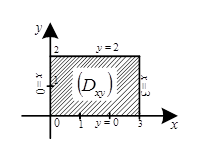
Рис. 10 Рис. 11
Сведением к повторному интегралу, вычислим двойной интеграл

 =
= 
Внутренний интеграл вычисляем при фиксированных значениях « ».
».
Тогда 
Отсюда по формуле Ньютона - Лейбница получим

Следовательно, среднее значение функции 
Ответ: 1.
ТРОЙНОЙ ИНТЕГРАЛ.
Тройной интеграл - обобщение определенного интеграла на трехмерную область  . Как и в двойном интеграле, он сводится к повторному (трехкратному) интегралу от непрерывной функции
. Как и в двойном интеграле, он сводится к повторному (трехкратному) интегралу от непрерывной функции 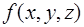 по правильной области
по правильной области 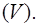 Область
Область  называется правильной, если прямые, проведенные через любую внутреннюю точку области параллельно координатным осям, пересекают границу области не более, чем в двух точках.
называется правильной, если прямые, проведенные через любую внутреннюю точку области параллельно координатным осям, пересекают границу области не более, чем в двух точках.
Объем области  выражается тройным интегралом
выражается тройным интегралом
 .
.
Задание 7. Изобразить проекцию области  на координатную плоскость
на координатную плоскость  и область интегрирования
и область интегрирования  . Вычислить объем тела, ограниченного поверхностями:
. Вычислить объем тела, ограниченного поверхностями: 
Решение.
На рис. 11, 12, 13 изображены проекции области  на координатные плоскости
на координатные плоскости 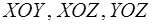 , на рис. 14 - область
, на рис. 14 - область  .
.


Рис. 12 Рис. 13

Рис. 14
Объем тела вычисляем по формуле:  .
.
Перейдем к повторному интегралу:
 .
.
Вычисляем внутренний интеграл при постоянных значениях  и
и  :
:

Переходим к повторному интегралу по области  :
:

Вычисляем внутренний интеграл по переменной 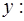

 Ответ: 4 (куб. ед.).
Ответ: 4 (куб. ед.).
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ