Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Оренбургский государственный педагогический университет»
Непротиворечивость аксиоматики геометрии Н. И. Лобачевского
Номинация: «Лучшая научно-исследовательская работа по математике»
Автор: Тугушева Д.Р.
Руководитель: Сафарова Алия Дамировна, к.п.н., доцент
г. Оренбург, 2020
Цель исследования: рассмотреть особенности доказательства непротиворечивости планиметрии Н. И. Лобачевского.
Объект исследования: геометрия Лобачевского.
Предмет исследования: доказательство непротиворечивости планиметрии Лобачевского.
Затянувшееся на две тысячи лет доказательство пятого постулата Евклида - одна из самых драматичных страниц в истории геометрии. Многочисленные попытки доказать постулат заставили «математический свет» усомниться в его справедливости. Наш соотечественник Н. И. Лобачевский хотел найти доказательство постулата методом от противного, предположив, что он неверен. Из этого предположения великому геометру удалось извлечь ряд непротиворечащих друг другу следствий, Н. И. Лобачевский пришёл к выводу, что, заменив пятый постулат Евклида его противоположностью, можно построить новую геометрию, столь же фундаментальную, что и геометрия Евклида.
Рассмотрим аксиоматику плоскости Лобачевского, докажем её непротиворечивость. Известно, что первые четыре постулата Евклида верны и для гиперболической геометрии. Аксиоматика так называемой абсолютной геометрии впервые была разработана Давидом Гильбертом (1962-1943) в труде «Основания геометрии», выпущенном в 1899 году.
В аксиоматике геометрии рассматривают такие объекты, как «точка», «прямая», а также «плоскость» и такие отношения, как «принадлежность», «между», «конгруэнтность».
Аксиоматика плоскости Лобачевского состоит из пяти групп:
I. Аксиомы сочетания
I1. Две различные точки А и В всегда определяют прямую а.
I2. Любые две различные точки прямой определяют эту прямую.
I3. Каждой прямой a принадлежат по крайней мере две точки.
I4. Существуют по крайней мере три точки, не принадлежащие одной прямой.
II. Аксиомы порядка
II1. Если А, В, С – три различные точки прямой а и точка В лежит между А и С, то точка В лежит также между С и А.
II2. Если А и В – точки прямой а, то существует по меньшей мере одна такая точка С, что В лежит между А и С.
II3. Из трех точек А, В, С прямой а существует не более одной, которая лежит между двумя другими.
III. Аксиомы конгруэнтности
III1. Если A, B – две точки на прямой a и A' – точка на той же прямой или на другой прямой a', то всегда можно найти по данную от точки А' сторону прямой а' одну и только одну такую точку В', что отрезок АВ конгруэнтен отрезку А'В'.
III2. Если отрезки А 'B' и А''В'' конгруэнтны одному и тому же отрезку АВ, то  .
.
III3. Пусть АВ и ВС – два отрезка прямой а без общих внутренних точек и пусть A  B
B  и В
и В  С
С  - два отрезка прямой а
- два отрезка прямой а  (отличной от а
(отличной от а  или с ней совпадающей) также без общих внутренних точек.
или с ней совпадающей) также без общих внутренних точек.
(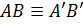 ,
, 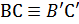 , то
, то 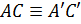 )
)
III4. Каждый угол конгруэнтен самому себе: Ð (h, k)  Ð (h, k) и Ð (h, k)
Ð (h, k) и Ð (h, k)  Ð (k, h)
Ð (k, h)
Отметим, что углом называется пара полупрямых h, k, выходящих из одной и той же точки О и не принадлежащих одной прямой. Полупрямые h и k называются сторонами угла, точка О – вершиной.
III5. Если для двух треугольников АВС и А  B
B  C
C  имеют место конгруэнции: АВ
имеют место конгруэнции: АВ  А
А  В
В  , АС
, АС  А
А  С
С  , Ð ВАС
, Ð ВАС 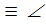 В
В  А
А  С
С  , то Ð АВС
, то Ð АВС  Ð А
Ð А  В
В  С
С  и Ð АСВ
и Ð АСВ  Ð А
Ð А  С
С  В
В  .
.
Любопытно, что среди аксиом Евклида нет аксиомы, соответствующей аксиоме III1, а также то, что аксиомы Евклида относятся к любым величинам, аксиомы Гильберта же только к отрезкам.