Научно-исследовательская практика часто нуждается в замене табличных функций, полученных экспериментально аналитическим выражением. Именно так решаются задачи интерполирования, численного дифференцирования и интегрирования. Однако, наличие погрешностей в этих данных не позволяет подобрать аналитические выражения, дающие график строго по экспериментальным точкам (например, при «точечном интерполировании» или при построении интерполяционных сплайнов). Уменьшить влияние этих погрешностей можно, если пользоваться для аппроксимации наблюденных зависимостей одной величины от другой более гладкой кривой, чем это дает опыт.
Допустим, что реально существует зависимость переменной Y от t, но эта зависимость имеет m степеней свободы, т.е. содержит m неизвестных параметров, которые нужно подобрать. Предположим, что наблюдения Y дают ряд приближенных значений 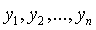 полученных при n различных значениях t. Неизвестные параметры обозначим через
полученных при n различных значениях t. Неизвестные параметры обозначим через 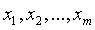 .
.
Итак, задача состоит в том, чтобы определить оценки параметров 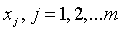 по заданному наблюдениями ряду
по заданному наблюдениями ряду 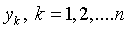 . Запишем постановку задачи в математических формулах
. Запишем постановку задачи в математических формулах 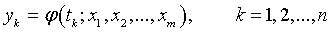
При m > n эта задача невыполнима, так как имеет бесчисленное множество решений. При m = n система может иметь однозначное решение, а при m < n - число уравнений больше числа неизвестных и уравнения, вообще говоря, несовместны. Именно к этому случаю применяется метод наименьших квадратов (МНК), которому посвящается данная глава.
4.1. Применение МНК к линейным функциям
Рассмотрим частный случай зависимости наблюдаемой величины l(t) от искомых параметров 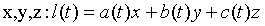 .
.
В дискретных значениях аргумента 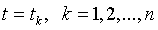 получим n значений
получим n значений 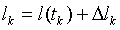 , где
, где 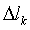 - ошибка измерения величины l в момент
- ошибка измерения величины l в момент 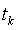 . Обозначим
. Обозначим 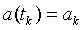 ,
,  ,
,  . Теперь для определения искомых x, y, z будем иметь систему n уравнений:
. Теперь для определения искомых x, y, z будем иметь систему n уравнений: 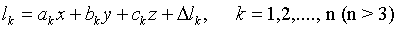 .
.
Критерий L2 будет выглядеть следующим образом: 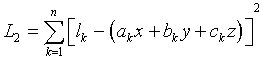 .
.
Построим систему нормальных уравнений:
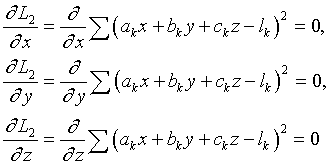 . .
|
Выполнив дифференцирование, получим
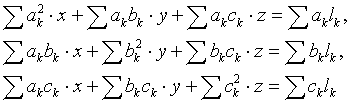 . .
|
Имеем систему, состоящую из трех линейных уравнений с тремя неизвестными, которую легко тем или иным способом решить.
Для обозначения сумм произведений или квадратов Гаусс предложил применять прямые скобки следующим образом 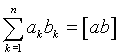 ,
, 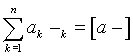 ,
, 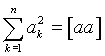 и т.д.
и т.д.
В этих обозначениях нормальные уравнения примут вид
 . .
|
Основное свойство нормальных уравнений - симметричность матрицы системы:
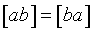 , , 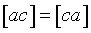 , , 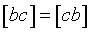 . .
|
Решить эту систему можно используя, формулы Крамера, или матричный способ.
4.2. Ковариационная матрица ошибок неизвестных
Поскольку суммы 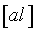 ,
, 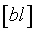 ,
, 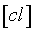 содержат ошибки наблюдений
содержат ошибки наблюдений 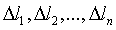 , то вычисленные из нормальных уравнений неизвестные x, y, z также будут содержать ошибки. Следовательно, нашим решением будет лишь оценки неизвестных
, то вычисленные из нормальных уравнений неизвестные x, y, z также будут содержать ошибки. Следовательно, нашим решением будет лишь оценки неизвестных 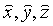 . Запишем нормальные уравнения в матричной форме
. Запишем нормальные уравнения в матричной форме
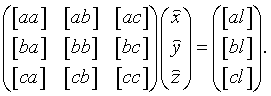
|
Очевидно, что погрешности неизвестных подчиняются той же системе уравнений
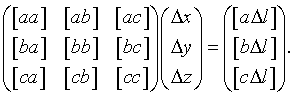
|
где элементы матрицы-столбца в правой части уравнений нужно понимать так
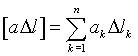 , , 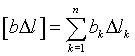 , , 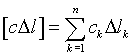 . .
|
Обозначим матрицу нормальных уравнений для краткости буквой Ф. Получим
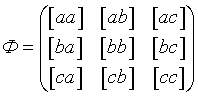 , , 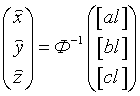 , , 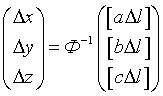 . .
|
Пусть наблюдения являются равноточными и независимыми. Тогда ковариационная матрица ошибок измерений ряда 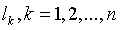 является диагональной
является диагональной
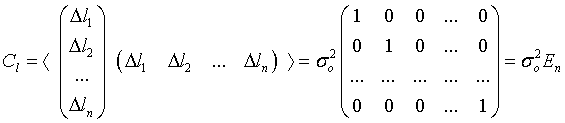 . .
|
Через En обозначена единичная матрица 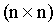 . Теперь образуем ковариационную матрицу ошибок оценок неизвестных:
. Теперь образуем ковариационную матрицу ошибок оценок неизвестных:
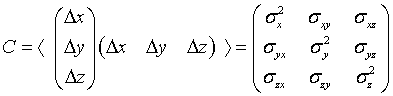 . .
|
где  - дисперсии ошибок неизвестных,
- дисперсии ошибок неизвестных, 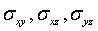 - ковариации этих неизвестных. Сразу же отметим, что если исходные данные представляют собой независимые наблюдения, то ошибки неизвестных не будут независимыми и их ковариации, вообще говоря, не равны нулю.
- ковариации этих неизвестных. Сразу же отметим, что если исходные данные представляют собой независимые наблюдения, то ошибки неизвестных не будут независимыми и их ковариации, вообще говоря, не равны нулю.
Используя решение нормальных уравнений для ошибок  , получим
, получим
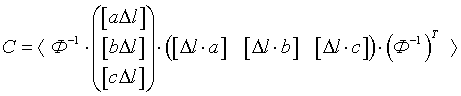 . .
|
Вследствие симметричности матрицы Ф ее обратная матрица также симметрична, и их транспонирование не изменяет.
Поскольку матрица Ф-1 не содержит случайных погрешностей, ковариационную матрицу ошибок неизвестных можно переписать так
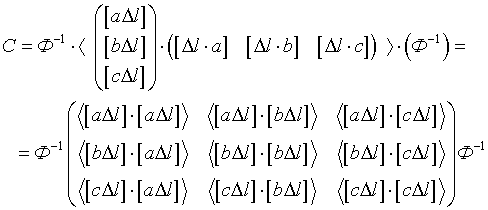 . .
|
Распишем первый элемент средней матрицы подробнее
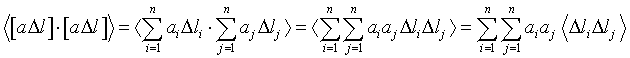 . .
|
Но вследствие равноточности и независимости измерений li и lj
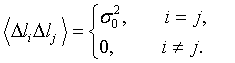 . .
|
Следовательно, в двойной сумме следует оставлять только те члены, у которых i = j. Будем иметь 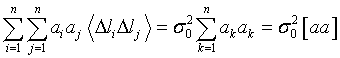 .
.
Точно также можно показать
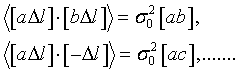 . .
|
Итак, ковариационная матрица ошибок неизвестных имеет вид
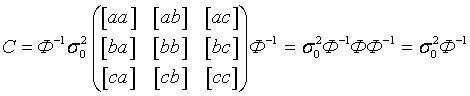 . .
|
Мы получили, таким образом, важную формулу, позволяющую вычислить не только дисперсии ошибок неизвестных, но и их ковариации 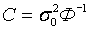 .
.
Сравним полученную формулу с формулой для дисперсии ошибки единичного измерения xk, имеющего вес pk (см. гл. 5) 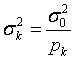
Видим полную аналогию. Роль дисперсии ошибки измерений играет ковариационная матрица ошибок неизвестных, а роль веса - матрица нормальных уравнений. Иными словами: матрица нормальных уравнений есть матричный вес вектора неизвестных.
4.3. Вычисление ошибок неизвестных
Обозначим элементы обратной матрицы Ф-1 через qij, т.е.
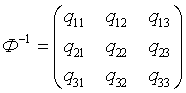 . Тогда . Тогда 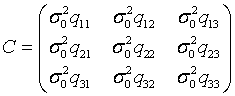 . .
|
Здесь диагональные элементы - дисперсии ошибок неизвестных: 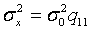 ,
, 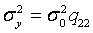 ,
, 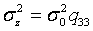 а недиагональные - их ковариации:
а недиагональные - их ковариации: 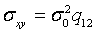 ,
, 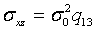 ,
, 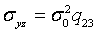 .
.
Постоянные 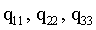 называют также весовыми коэффициентами (в отличие от весов неизвестных px, py, pz). Чтобы получить веса неизвестных, нужно найти обратную величину
называют также весовыми коэффициентами (в отличие от весов неизвестных px, py, pz). Чтобы получить веса неизвестных, нужно найти обратную величину 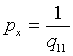 ,
, 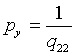 ,
, 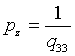 .
.
В подавляющем большинстве случаев нам нужно определить среднеквадратические ошибки МНК-оценок неизвестных. В этом случаае вычисляют СКО «единицы веса» по формуле, которую мы введем несколько позже: 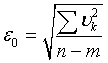 , где
, где 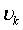 - остаточные разности:
- остаточные разности:  , а m - число неизвестных (m = 3).
, а m - число неизвестных (m = 3).
Величина 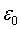 , как правило, заменяет стандартное отклонение
, как правило, заменяет стандартное отклонение 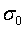 и является его несмещенной оценкой. Поэтому СКО неизвестных определяют по формулам
и является его несмещенной оценкой. Поэтому СКО неизвестных определяют по формулам
 , ,  , , 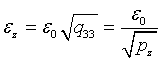 . .
|
Для системы трех уравнений веса неизвестных легко вычислить, образуя матрицу Ф.
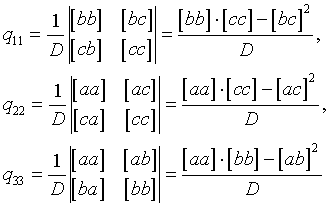
|
Веса px, py, pz - соответственно - отношения определителя системы к определителю матрицы, полученной вычеркиванием соответствующих строки и столбца, где расположен диагональный элемент обратной матрицы нормальных уравнений.
Пример. Решим систему уравнений 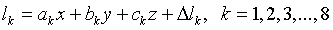 . Численные значения
. Численные значения 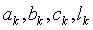 сведены в таблицу
сведены в таблицу
| ak | bk | ck | lk | 
| 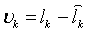
|
| 6.8 | +0.2 | ||||
| -2 | 0.8 | +0.2 | |||
| -1 | 3.9 | -0.9 | |||
| -1 | 2.2 | -0.2 | |||
| -2 | 0.6 | +0.4 | |||
| -2 | -1 | 5.4 | +0.6 | ||
| -2 | 0.8 | +0.2 | |||
| 5.2 | -0.2 |
Составим нормальные уравнения. Первый элемент матрицы нормальных уравнений есть сумма квадратов элементов первого столбца (ak), второй элемент первой строки есть сумма произведений элементов второго и первого столбцов 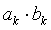 , и т.д. Получим
, и т.д. Получим
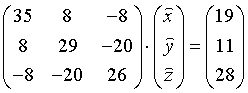
Решим полученную систему методом обращения матриц:
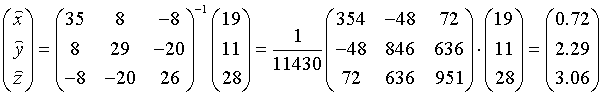
Минимальная сумма квадратов разностей равна 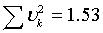 , т.е.
, т.е.  .
.
Определим веса неизвестных 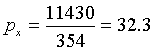 ,
, 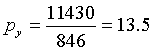 ,
, 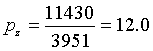 .
.
Отсюда 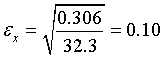 ,
, 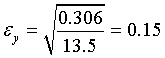 ,
, 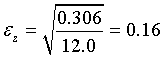 .
.
Решение следует записать в виде 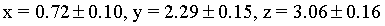 .
.
4.4. Приведение уравнений МНК с неравноточными наблюдениями к равноточным
Нормальные уравнения с неравноточными наблюдениями имеют более сложный вид, чем это предусмотрено, например, схемой Гаусса. Существует простая операция, которая позволяет преобразовать исходные уравнения так, что “наблюдения” становятся равноточными.
Пусть 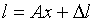 , где А - матрица
, где А - матрица 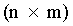 , х - вектор искомых параметров
, х - вектор искомых параметров 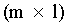 , l и
, l и 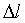 - вектора наблюдений и погрешностей
- вектора наблюдений и погрешностей 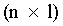 .
.
Если наблюдения независимы, то ковариационная матрица ошибок имеет вид
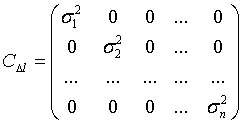
Поскольку вес каждого наблюдения обратно пропорционален дисперсии 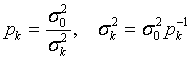 , то
, то
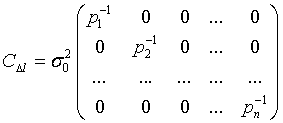
Обозначим.

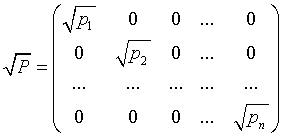
Умножим исходное матричное уравнение слева на  . Получим
. Получим 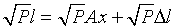 . Обозначим
. Обозначим 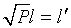 ,
, 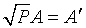 ,
, 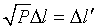 . Теперь
. Теперь 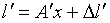 причем ковариационная матрица вектора погрешностей
причем ковариационная матрица вектора погрешностей 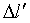 имеет вид
имеет вид
 . .
|
Мы получили, таким образом, ковариационную матрицу ошибок независимых равноточных наблюдений. К системе исходных уравнений, отмеченной штрихами, применима любая методика решения уравнений в методе наименьших квадратов.
Умножение слева на диагональную матрицу  равносильно умножению каждой k -той строки исходных уравнений на
равносильно умножению каждой k -той строки исходных уравнений на 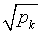 . Система
. Система 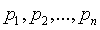 должна быть задана.
должна быть задана.
МНК может быть применен и к системе с зависимыми наблюдениями, но в этом случае ковариационная матрица погрешностей наблюдений перестает быть диагональной и описанная здесь методика становится неприменимой.