Лекция 6(9)
Значимость параметров уравнения прямолинейной регрессии.
Доверительная зона регрессии
Общее варьирование значений функционального признака можно рассматривать, с одной стороны, как результат зависимости yi от xi, а с другой – как результат случайной вариации, вызываемой неизвестными факторами. То есть можно общую сумму квадратов с соответствующим ей числом степеней свободы 
:
разложить на две составляющие:
– одна из них с числом степеней свободы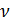 
=1 связана с существованием регрессии y/x и равна:
– вторая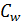 
с числом степеней свободы 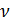=n-2 связана с влиянием случайных факторов. Она равна:
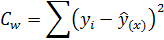
С практической точки зрения полезно знать, что существует ряд равноценных формул для вычисления:
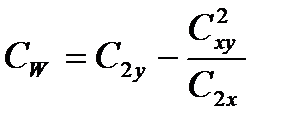
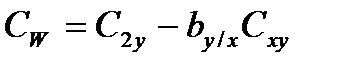
Эта сумма называется остаточной или случайной. Этой сумме соответствует 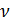=n-2 степеней свободы, поэтому дисперсия Sw2, оценивающая случайное варьирование значений yi вокруг линии регрессии y/x, оказывается равной
Среднее квадратическое отклонение sW имеет важное значение для оценки значимости параметров уравнения регрессии 
и b и для построения доверительной зоны регрессии.
Располагая результатами выборочных наблюдений для генеральных значений параметров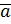 
и 
можно вычислить лишь выборочные оценки и b, отягощённые соответствующими ошибками репрезентативности Sa и Sb, которые можно оценить по формулам:
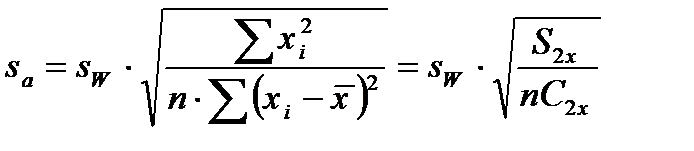
или
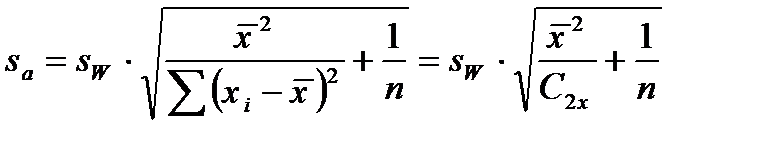
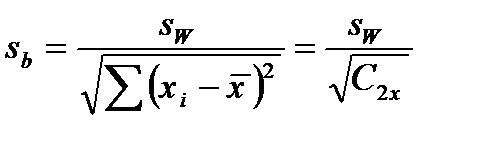
b определяет угол наклона линии регрессии, а – местоположение линии регрессии относительно оси y.
Если связь между признаками отсутствует, то угловой коэффициент b=0.
Поэтому для оценки значимости наличия связи можно воспользоваться способом проверки нулевой гипотезы, состоящей в предположении, что =0. Поскольку отношение
можно считать распределённым как t-Стьюдента, с 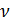=n-2 степенями свободы, то при условии
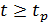
нулевая гипотеза отвергается и с соответствующей вероятностью признаётся, что генеральный коэффициент регрессии отличен от нуля, а, значит, связь между признаками существует.
Доверительные границы для можно найти согласно формуле:
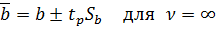
Значимость отличия от нуля ( никогда не равен нулю в силу случайных вариаций) также проверяется с помощью критерия Стьюдента: если отношение
для 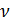=n-2, то с соответствующей вероятностью можно утверждать, что не случайно отличен от нуля, и => линия регрессии значимо не проходит через начало координат. Если t<tp, то нулевая гипотеза 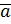=0 не отвергается и можно считать, что уравнение регрессии имеет вид:
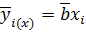
Примечание: выборочная оценка коэффициента регрессии в уравнении подобного вида может быть найдена согласно:
а ошибка такого коэффициента ϭb определяется по формуле
Она обычно меньше ошибки 
, вычисленной по предыдущему уравнению, что является результатом соблюдения условия прохождения линии регрессии через начало координат, ограничивающего вариацию величины b.
В общем виде доверительные границы для 
, когда уравнение регрессии имеет вид:
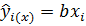
определяются согласно:
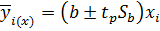
Для уравнения вида
доверительная зона регрессии средних определяется более сложно. В этом случае линии, ограничивающие доверительную зону регрессии, представляют собой гиперболы. В общем виде доверительные границы для можно найти по выражению
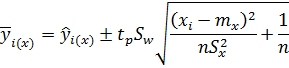
здесь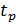 
соответствует заданной доверительной вероятности p при 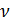=n-2
Из формулы следует, что ширина доверительного интервала для возрастает по мере увеличения абсолютной величины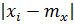 
. Минимум ширины доверительная зона регрессии средних имеет при xi=mx:
Если 
не являются случайными величинами, а задаются произвольно, то доверительные границы для можно определить согласно:
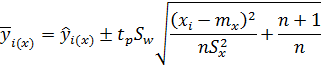
При xi=mx формула эта приобретает вид
