4×n + 3). Если простое число р = 4×n+3 делит сумму квадратов двух натуральных чисел, то оно делит каждое из этих чисел.
Доказательство. От противного. Пусть x2 +y2º0(mod p), но x 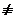 0(mod p) или y
0(mod p) или y 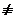 0 (mod p). Поскольку x и y симметричны, их можно менять местами, так что можно предполагать, что x
0 (mod p). Поскольку x и y симметричны, их можно менять местами, так что можно предполагать, что x 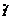 p.
p.
Лемма (об обратимости по модулю p). Для любого целого числа x, не делящегося на простое число p, существует обратный элемент по модулю p – такое целое число 1 £ u < p, что x×u º 1 (mod p).
Доказательство. Число x взаимно простое с p, поэтому можно записать линейное разложение НОД(x, p) = 1 = x×u + p×v (u, v Î Z). Ясно, что x×uº1(modp), т.е. u – обратный элемент к x по модулю p. Если u не удовлетворяет ограничению 1 £ u < p, то поделив u с остатком на p, получим остаток r º u (mod p), для которого x×r º x×u º 1 (mod p) и 0 £ r < p.
Лемма об обратимости по модулю p доказана.
Умножая сравнение x2 + y2 º 0 (mod p) на квадрат u2 обратного элемента к x по модулю p, получим 0 = 0×u2 º x2×u2 + y2×u2 = (x×u)2 + (y×u)2 º 1 + t2 (mod p).
Таким образом, для t = y×u выполнено сравнение t2 º –1 (mod p), которое и приведём к противоречию. Ясно, что t 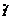 p: иначе t º 0 (mod p) и 0 º t2 º –1 (mod p), что невозможно. По теореме Ферма имеем t p–1 º 1 (mod p), что вместе с t2 º –1 (mod p) и p = 4×n + 3 приводит к противоречию:
p: иначе t º 0 (mod p) и 0 º t2 º –1 (mod p), что невозможно. По теореме Ферма имеем t p–1 º 1 (mod p), что вместе с t2 º –1 (mod p) и p = 4×n + 3 приводит к противоречию:
1 º t p–1 = t 4×n+3–1 = t 2×(2×n+1) = (t 2)2×n+1 º (–1)2×n+1 = –1 (mod p).
Полученное противоречие показывает, что допущение о x 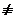 0 (mod p) было не верным.
0 (mod p) было не верным.
Лемма о делимости суммы двух квадратов на простое число 4×n+3 доказана.
Таким образом, доказано, что число, в каноническое разложение которого входит простое число p = 4×n + 3 в нечётной степени, не представимо в виде суммы двух квадратов.
Докажем теперь, что любое число, в каноническом разложении которого простые числа p = 4×n + 3 участвуют только в чётных степенях, представимо в виде суммы двух квадратов.
Идея доказательства основана на следующем тождестве:
(а2 + b2)×(c2 + d2) = (a×c – b×d)2 + (a×d + b×c)2,
которое можно получить из известного свойства модуля комплексных чисел – модуль произведения равен произведению модулей. Действительно,
|z|×|t| = |z×t| Û |a + b×i|×|c + d×i| = |(a + b×i)×(c + d×i)| Û
Û |a + b×i|2×|c + d×i|2 = |(a×c – b×d) + (a×d + b×c)×i|2 Û
Û (а2 + b2)×(c2 + d2) = (a×c – b×d)2 + (a×d + b×c)2.
Из этого тождества следует, что если два числа u, v представимы в виде суммы двух квадратов: u = x2 + y2, v = z2 + t2, то и их произведение u×v представимо в виде суммы двух квадратов: u×v = (x×z – y×t)2 + (x×t + y×z)2.
Любое натуральное число a > 1 можно записать в виде a = р1× … ×рk×m2, где рi – попарно различные простые числа, m Î N. Для этого достаточно найти каноническое разложение 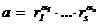 , записать каждую степень вида ra в виде квадрата (rb)2 при чётном a = 2×b, или в виде ra = r×(rb)2 при нечётном a = 2×b + 1, а затем сгруппировать отдельно квадраты и оставшиеся одиночные простые числа. Например,
, записать каждую степень вида ra в виде квадрата (rb)2 при чётном a = 2×b, или в виде ra = r×(rb)2 при нечётном a = 2×b + 1, а затем сгруппировать отдельно квадраты и оставшиеся одиночные простые числа. Например,
29250 = 2×32×53×13 = 2×5×13×(3×5)2, m = 15.
Число m2 обладает тривиальным представлением в виде суммы двух квадратов: m2 = 02 + m2. Если доказать представимость в виде суммы двух квадратов всех простых чисел рi (1 £ i £ k), то используя тождество, будет получено и представление числа a. По условию, среди чисел р1, …, рk могут встретиться только 2 = 12 + 12 и простые числа вида 4×n + 1. Таким образом, осталось получить представление в виде суммы двух квадратов простого числа р = 4×т + 1. Это утверждение выделим в отдельную теорему (см. ниже)
Например, для a = 29250 = 2×5×13×(15)2 последовательно получаем:
2 = 12 + 12, 5 = 12 + 22, 13 = 22 + 32,
2×5 = (1×1 – 1×2)2 + (1×2 + 1×1)2 = 12 + 32,
2×5×13 = (1×2 – 3×3)2 + (1×3 + 3×2)2 = 72 + 92,
29250 = 2×5×13×(15)2 = (7×15)2 + (9×15)2 = 1052 + 1352.
Теорема доказана.
§ 4. Уравнение х 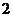 + х + 1 = 3×у
+ х + 1 = 3×у 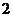
Займемся теперь уравнением х 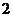 +x+1=Зу
+x+1=Зу 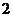 . Оно уже имеет свою историю. В 1950 г. Р. Облат высказал предположение, что, кроме решения
. Оно уже имеет свою историю. В 1950 г. Р. Облат высказал предположение, что, кроме решения
x=у=1. оно не имеет иных решений в натуральных числах х, у, где х есть нечетное число. В том же году Т. Нагель указал решение x = 313, у =181. Метод, аналогичный изложенному выше для уравнения х 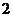 +х-2у
+х-2у 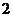 =0, позволит нам определить все решения уравнения x
=0, позволит нам определить все решения уравнения x 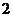 +х+1=3у
+х+1=3у 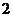 (1)
(1)
в натуральных числах x, у. Предположим, что (х, у) есть решение уравнения (1) в натуральных числах, причем х > 1. Можно легко убедиться, что уравнение(18) не имеет решений в натуральных числах x, у, где х = 2, 3. 4, 5, 6, 7, 8, 9; поэтому должно быть х 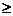 10.
10.
Покажем, что 12у<7x+3, 7у>4x + 2. 4у> 2x+1. (2)
Если бы было 12y > 7x+3, мы имели бы 144у 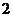 > 49x
> 49x 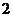 +42x+9. а так как, в виду (18), 144у
+42x+9. а так как, в виду (18), 144у 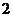 = 48x
= 48x 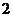 + 48x + 48, то было бы х
+ 48x + 48, то было бы х 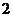 < 6x +3 9, откуда
< 6x +3 9, откуда
(х-З) 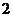 < 48 и, значит, учитывая, что x > 10, 7
< 48 и, значит, учитывая, что x > 10, 7 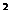 < 148, что невозможно. Итак, первое из неравенств (2) доказано.
< 148, что невозможно. Итак, первое из неравенств (2) доказано.
Если бы было 7у < 4x+2, мы имели бы 49у 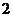 < 16x
< 16x 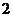 + 16x+4, а так как, ввиду (1), 16x
+ 16x+4, а так как, ввиду (1), 16x 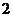 + 16x + 16 = 48у
+ 16x + 16 = 48у 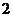 , то было бы 49у
, то было бы 49у 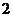 < 48у
< 48у 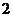 - 12, что невозможно. Таким образом, доказано второе из неравенств (2), из которого уже непосредственно вытекает третье. Итак, неравенства (2) верны.
- 12, что невозможно. Таким образом, доказано второе из неравенств (2), из которого уже непосредственно вытекает третье. Итак, неравенства (2) верны.
Положим теперь
w = 7х — 12у+3, h = -4x + 7у-2. (3)
На основании (2), найдем, что w > 0, h > 0 и х — w=3(4y-2x-1)>0 и, значит, w<х. Согласно (3), имеем w2+w+1=3h2 откуда, ввиду (1), Примем g(x, у) = (7х- 12у + 3, -4x + 7у -2).
Итак, можно сказать, что, исходя из любого решения (х, у) уравнения (1) в натуральных числах, где х > 1, мы получаем новое решение (w,h) = g(x, у) уравнения (1) в натуральных числах w,h где w < х (и значит, решение в меньших натуральных числах). Отсюда, действуя как выше, найдем, что для каждого решения уравнения (1) в натуральных числах х, у, где х > 1, существует натуральное число n такое, что g  (x, y) = (l, 1).
(x, y) = (l, 1).
Приняв же f(x, у) = (7x+12у + 3, 4x + 7у + 2), (4) легко найдем, что f(g(x,y)) = (x, у) и, следовательно, (x,y) = f  (1,1) С другой стороны, легко проверить, что если (х, у) есть решение уравнения (1) в натуральных числах, то f(x,y) также есть решение уравнения (1) в натуральных числах (соответственно больших, чем х и у).
(1,1) С другой стороны, легко проверить, что если (х, у) есть решение уравнения (1) в натуральных числах, то f(x,y) также есть решение уравнения (1) в натуральных числах (соответственно больших, чем х и у).
Приняв x 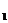 =y
=y 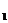 =1(x
=1(x  , y
, y  ) = f
) = f 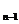 (1, 1) для n=2,3,…..,
(1, 1) для n=2,3,…..,
получим последовательность {x  ,y
,y  } для n= 1, 2,….., содержащую все решения уравнения (1) в натуральных числах и только такие решения.
} для n= 1, 2,….., содержащую все решения уравнения (1) в натуральных числах и только такие решения.
Здесь мы имеем (х 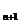 ,y
,y 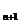 )= f
)= f  (1,1)=f(x
(1,1)=f(x  , y
, y  ), следовательно, в силу (4), получаем
), следовательно, в силу (4), получаем
х 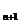 = 7x
= 7x  +12 y
+12 y  +3, y
+3, y 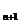 =4 x
=4 x  +7 y
+7 y  +2 (5) (n=1, 2,...)
+2 (5) (n=1, 2,...)
— формулы, позволяющие последовательно определять все решения (х, у) уравнения (1) в натуральных числах. Таким путем легко получаем решения (1,1),(22,13),(313,181),.(4366,2521),(60817,35113),..
Этих решений имеется, очевидно, бесконечное множество. Из равенств
х 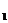 = у
= у 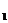 = 1 и (4) при помощи индукции легко находим, что числа х
= 1 и (4) при помощи индукции легко находим, что числа х  с нечетными индексами суть нечетные, с четными же — четные, а числа y
с нечетными индексами суть нечетные, с четными же — четные, а числа y  суть нечетные для n = 1, 2,... Для получения всех решений уравнения (1) в целых числах х, у, как нетрудно доказать, следовало бы к уже полученным решениям (x
суть нечетные для n = 1, 2,... Для получения всех решений уравнения (1) в целых числах х, у, как нетрудно доказать, следовало бы к уже полученным решениям (x  , y
, y  ) присоединить (x
) присоединить (x  , -y
, -y  ) и (-x
) и (-x  -1, ±y
-1, ±y  ) для n=1, 2,...
) для n=1, 2,...
Так что здесь мы имеем, например, еще такие решения: (—2,1) (—23,13), (—314,181). А. Роткевич заметил, что из всех решений уравнения (1) в натуральных числах х > 1 и у можно получить все решения уравнения (z+1) 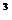 -z
-z 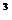 = y
= y 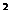 (6)
(6)
в натуральных числах z, у. В самом деле, допустим, что натуральные числа z,у удовлетворяют уравнению (5). Положив x=3z+l, получим, как легко проверить, натуральные числа х > 1 и у, удовлетворяющие уравнению (1).
С другой стороны, если натуральные числа х > 1 и у удовлетворяют уравнению (1), то имеем, как легко проверить, (х— 1) 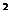 = 3(у
= 3(у 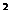 -х), откуда следует, что число (натуральное) х—1 делится на 3, следовательно х-1= 3 z, где z есть натуральное число, причем имеет место равенство 3z
-х), откуда следует, что число (натуральное) х—1 делится на 3, следовательно х-1= 3 z, где z есть натуральное число, причем имеет место равенство 3z 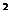 = y
= y 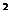 -x=у
-x=у 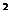 3z-1, которое доказывает, что числа z и у удовлетворяют уравнению (6). Таким образом, исходя из решений (22,13),(313,181), (4366,2521) уравнения (1), получаем решения (7,13),(104,181),(1455,2521) уравнения (6). Заметим здесь еще, что если натуральные числа z, у удовлетворяют уравнению (6), то доказано, что у есть сумма двух последовательных квадратов, например 13=2
3z-1, которое доказывает, что числа z и у удовлетворяют уравнению (6). Таким образом, исходя из решений (22,13),(313,181), (4366,2521) уравнения (1), получаем решения (7,13),(104,181),(1455,2521) уравнения (6). Заметим здесь еще, что если натуральные числа z, у удовлетворяют уравнению (6), то доказано, что у есть сумма двух последовательных квадратов, например 13=2 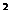 +3
+3 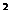 ,181=9
,181=9 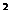 +10
+10 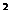 , 2521=35
, 2521=35 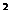 + 36
+ 36 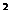 . Подобным образом, как прежде для уравнения(1), мы могли бы найти все решения уравнения x
. Подобным образом, как прежде для уравнения(1), мы могли бы найти все решения уравнения x 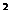 +(x+1)
+(x+1) 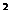 =y
=y 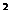 в натуральных числах х, у, приняв для х > 3 g(x. у) = (3х -2у+1, 3у - 4х- 2) и для x > 1 f(x, y) = (3x + 2y+l, 4х + Зу + 2), что приводит к формуле (х, у) f
в натуральных числах х, у, приняв для х > 3 g(x. у) = (3х -2у+1, 3у - 4х- 2) и для x > 1 f(x, y) = (3x + 2y+l, 4х + Зу + 2), что приводит к формуле (х, у) f  (3,5) и к выводу, что все решения уравнения (6) в натуральных числах х, у содержатся в последовательности {x
(3,5) и к выводу, что все решения уравнения (6) в натуральных числах х, у содержатся в последовательности {x  ,y
,y  } для n= 1, 2,…., где х
} для n= 1, 2,…., где х 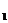 = 3, у
= 3, у 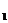 = 5, а x
= 5, а x 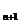 =3x
=3x  + 2y
+ 2y  +1. y
+1. y 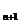 = 4 x
= 4 x  +3 y
+3 y  +2 (n=1, 2,...). Например, х
+2 (n=1, 2,...). Например, х 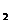 =3•3+2•5+1=20, у
=3•3+2•5+1=20, у 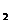 = 4•3+З•5 + 2 = 29; x
= 4•3+З•5 + 2 = 29; x 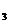 =119, у
=119, у 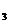 =169: x
=169: x 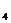 =69б, у
=69б, у 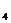 = 985; x
= 985; x 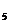 =4059, у
=4059, у 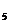 =5741.
=5741.
Геометрический смысл рассмотренного уравнения состоит в том, что оно дает все пифагоровы треугольники (прямоугольные с натуральными сторонами), катеты которых выражаются последовательными натуральными числами. Таких треугольников имеется бесконечное множество (*).
Уравнение же x 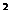 +(x+1)
+(x+1) 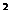 =y
=y 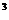 , как доказано, не имеет решений в натуральных числах х, у.
, как доказано, не имеет решений в натуральных числах х, у.
Пифагоровы тройки
Рассмотрим уравнение x2 + y2 = z2, представляющее собой соотношение Пифагора для прямоугольного треугольника. Вначале найдём все его рациональные решения, а затем – все целые решения диофантова уравнения.
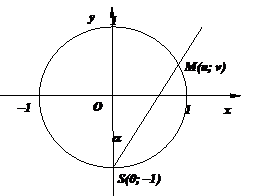 1. Рациональные решения. Во-первых, уравнение переписывается в виде
1. Рациональные решения. Во-первых, уравнение переписывается в виде 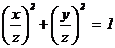 , где отношения
, где отношения  ,
, 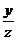 рациональны, если рациональными были x, y. Эти отношения являются рациональными координатами точек на единичной окружности. Точки с рациональными координатами на окружности назовём рациональными. Если все рациональные точки M(u; v) окружности каким-то образом описаны, то u2 + v2 = 1 и
рациональны, если рациональными были x, y. Эти отношения являются рациональными координатами точек на единичной окружности. Точки с рациональными координатами на окружности назовём рациональными. Если все рациональные точки M(u; v) окружности каким-то образом описаны, то u2 + v2 = 1 и  = u,
= u, 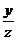 = v, т.е. x = z×u, y = z×v, где z Î Q. Таким образом, задача свелась к описанию всех рациональных точек окружности.
= v, т.е. x = z×u, y = z×v, где z Î Q. Таким образом, задача свелась к описанию всех рациональных точек окружности.
Изложим общий метод нахождения всех рациональных точек окружности, применимый и для многих других кривых, заданных полиномиальными уравнениями.
Выберем на кривой рациональную точку, например точку S(0; –1) на окружности. Если M(u; v) – произвольная рациональная точка, то рациональным будет и 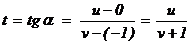 . Обратно, если t Î Q, то u = t×(v + 1) и u2 + v2 = 1, т.е. t2×(v + 1)2 + v2 = 1 или (t2+1)×v2+2×t2×v+t2- 1= 0. Здесь дискриминант D = 4×t4 – 4×(t4 – 1) = 4 и
. Обратно, если t Î Q, то u = t×(v + 1) и u2 + v2 = 1, т.е. t2×(v + 1)2 + v2 = 1 или (t2+1)×v2+2×t2×v+t2- 1= 0. Здесь дискриминант D = 4×t4 – 4×(t4 – 1) = 4 и 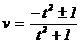 . Если взять знак минус, то получим v = –1, u = t×(v + 1) = 0, т.е. точку S(0; –1). Если же брать плюс, то
. Если взять знак минус, то получим v = –1, u = t×(v + 1) = 0, т.е. точку S(0; –1). Если же брать плюс, то 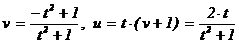 Î Q.
Î Q.
Таким образом, доказано, что точка на окружности рациональна тогда и только тогда, когда она либо совпадает с S(0; –1), либо получается по формулам 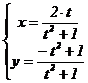 при некотором t Î Q.
при некотором t Î Q.
Легко понять, что точка S(0; –1) не может быть получена по приведённым формулам ни при каком рациональном t. Можно видоизменить параметризацию, чтобы включить точку S в общие решения. Для этого запишем рациональное число t в несократимом виде 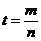 , где m Î Z, nÎN и НОД(m, n) = 1. Тогда формулы перепишутся так:
, где m Î Z, nÎN и НОД(m, n) = 1. Тогда формулы перепишутся так: 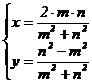 . Эти формулы определены при любых m, n Î Z и при n = 0 получаем точку
. Эти формулы определены при любых m, n Î Z и при n = 0 получаем точку
S(0;-1). Таким образом, доказана следующая теорема.
Теорема (о рациональных точках на окружности). (1) Все рациональные точки M(x; y) единичной окружности имеют координаты
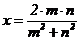 ,
, 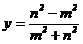 , при некоторых m, n Î Z, НОД(m, n) = 1.
, при некоторых m, n Î Z, НОД(m, n) = 1.
(2) Все рациональные пифагоровы тройки, т.е. рациональные решения уравнения x2 + y2 = z2 задаются формулами 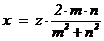 ,
, 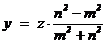 , где m, n Î Z и НОД(m, n) = 1, z Î Q.
, где m, n Î Z и НОД(m, n) = 1, z Î Q.
2. Целые решения. Рассмотрим диофантово уравнение x2 + y2 = z2 от трёх неизвестных x, y, z. Оно, конечно, имеет решения: например, (0; 0; 0), (0; 1; 1), (3; 4; 5) и множество других. Решения, в которых одно из чисел равно нулю, называются тривиальными. Ясно, что все тривиальные решения имеют вид: (0; y; ±y), (x; 0; ±x). Достаточно искать только нетривиальные решения.
Кроме того, назовём решение (x; y; z) примитивным, если любые два числа в нём взаимно просты, т.е. если НОД(x, y) = НОД(x, z) = НОД(y, z) = 1. Ясно, что если есть некоторое решение (x; y; z) и D = НОД(x, y, z), то
x = D×x1, y = D×y1, z = D×z1 при некоторых целых x1, y1, z1, причём ввиду x2 + y2 = z2 получаем, сокращая на D2, x12 + y12 = z12, т.е. тройка (x1; y1; z1) тоже является решением. Кроме того, это решение примитивно. Действительно, если НОД(x, y) = d > 1, то x1 = d×x2, y1=d×y2 и d2×(x22+y22)= z12 и число z1 делится на любой простой делитель p числа d, вопреки взаимной простоте чисел x1, y1, z1. Аналогично рассматриваются и другие возможности НОД(x, z) > 1, НОД(y, z) > 1.
Итак, доказано, что любое решение получается из примитивного умножением всех его компонент на некоторое натуральное число D. Поэтому достаточно искать лишь примитивные пифагоровы тройки. Поскольку каждая такая тройка состоит из рациональных чисел, то можно применить описание рациональных пифагоровых троек.
Прежде всего, заметим, что из x2 + y2 = z2 следует, что одно из чисел x, y чётно, а другое нечётно. Действительно ввиду примитивности тройки x, y не могут быть чётными одновременно. Если x, y оба нечётны, то x2 + y2 чётно, т.е. z чётно и x2 + y2 делится на 4, что ведёт к противоречию: если x=2×u+1, y = 2×v + 1 (u, v Î Z), то x2 + y2 = 4×(u2 + u + v2 + v) + 2 и не делится на 4.
Поменяв, если нужно, x, y местами, будем считать, что x чётно, а y нечётно. Согласно предыдущей теореме, каждая примитивная тройка (x; y; z) имеет вид 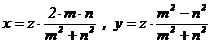 при целых z, m, n, НОД(m, n) = 1. Значит, x×(m2 + n2) = z×2×m×n, причём числа x и z взаимно простые. По основному свойству взаимно простых чисел m2 + n2 = z×t (t Î Z) и x×t =2×m×n, y =
при целых z, m, n, НОД(m, n) = 1. Значит, x×(m2 + n2) = z×2×m×n, причём числа x и z взаимно простые. По основному свойству взаимно простых чисел m2 + n2 = z×t (t Î Z) и x×t =2×m×n, y = 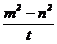 , т.е. m2 – n2 = y×t. Отсюда 2×m2 = (z + y)×t, 2×n2 = (z – y)×t, т.е. t– общий делитель чисел 2×m2 и 2×n2. Поэтому t делит НОД(2×m2,2×n2)=2×НОД(m2,n2)=2.
, т.е. m2 – n2 = y×t. Отсюда 2×m2 = (z + y)×t, 2×n2 = (z – y)×t, т.е. t– общий делитель чисел 2×m2 и 2×n2. Поэтому t делит НОД(2×m2,2×n2)=2×НОД(m2,n2)=2.
Если t = ±2, то m2 + n2 = ±2×z M 2, т.е. взаимно простые числа m, n оба нечётны, и кроме того, ±2×x=2×m×n, т.е. x= ±m×n – нечётно, вопреки выбору x.
Значит, t = ±1, x = ±2×m×n, y = ±(m2 – n2), z = ±(m2 + n2), где целые числа m, n взаимно простые разной чётности (иначе y чётно), а комбинации знаков – любые. Учитывая возможность поменять местами x, y, получаем ещё возможность x = ±(m2 – n2), y = ±2×m×n, z = ±(m2 + n2). Любая целочисленная тройка получается одновременным умножением компонент описанных выше примитивных троек на произвольное целое число.
Таким образом, доказана
Теорема (о пифагоровых тройках). Любая пифагорова тройка имеет один из следующих видов:
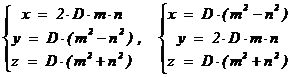 ,
,
где D, m, n – целые числа, m и n взаимно простые разной чётности.
Великая теорема Ферма
Из истории проблемы. Сочинение Диофанта, изданное в 1621 году в переводе Клода Гаспара де Баше де Мазирьяка (1581-1630), дало повод Пьеру Ферма записать на полях перевода одно из самых достопримечательных замечаний в истории математики:
“Невозможно разложить куб на два куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две степени с тем же самым показателем; я нашел этому поистине чудесное доказательство, однако поля слишком малы, чтобы оно здесь уместилось”.
Таким образом, большая или Великая теорема Ферма утверждает, что уравнение xn + yn = zn, ни при каком натуральном n, большем двух, неразрешимо в целых положительных числах.
В 1908 году Пауль Вольфскель завещал премию в 100 тысяч германских марок тому, кто первым представит доказательство. В результате инфляции после первой мировой войны величина премии в настоящее время ничтожна. К тому же как указывает Г. Эдвардс в своей книге о теореме Ферма, премия была назначена лишь за доказательство предположения – нахождение контрпримера не принесло бы ни пфеннига его открывателю!
После объявления о премии Великой теоремой Ферма занялись не только профессионалы, но и широкая публика. Так как в условие награждения входило требование, чтобы доказательство было опубликовано, а научные издательства не желали принимать ложных доказательств, то авторы печатали свои доказательства на собственный счет. Так во многих странах, в том числе и в России, появилось много печатных неправильных доказательств Великой теоремы Ферма.
Общим свойством этих “доказательств” является то, что они ошибочны уже для наименьшего показателя в теореме Ферма, а именно, для показателя n = 3. Авторы этих работ, преимущественно не математики, оперировали только элементарными средствами. Между тем, известное правильное доказательство уже для показателя n = 3 является неэлементарным.
Справедливость Великой теоремы Ферма для некоторых частных случаев была установлена уже довольно давно: сам Ферма оставил доказательство отсутствия нетривиальных решений уравнения хn + yn = zn при n = 4, Л. Эйлер доказал теорему Ферма для n = 3 (1770 г), А. Лежандр – при n = 5 (1825 г), и Г. Лаше – для n = 7 (1839 г).
Замечательные продвижения принадлежат Э. Куммеру (1810-1893), который своими исследованиями по проблеме Ферма оказал решающее влияние на развитие алгебраической теории чисел. В XX столетии его методы были усовершенствованы и дополнены (1929 г. и позже) прежде всего благодаря усилиям У. Вандивера, Д. Лемера и Э. Лешера. К 80-м годам XX в. с использованием ЭВМ неразрешимость уравнения хn + yn = zn в натуральных числах была установлена для всех n £ 2125000 (З. Вагштафф, 1976 г.). Если принять во внимание, что число 2125000 записывается 37628-ю цифрами, то поиски контрпримера к Великой теореме Ферма представлялись совершенно безнадежным занятием.
23 июня 1993 г. математик из Принстона Эндрю Уайлс в докладе на конференции по теории чисел в Кембридже (Великобритания) анонсировал решение проблемы Ю. Таниямы (о модулярности эллиптических кривых с рациональными коэффициентами). Ранее уже было доказано (в 1985 г. Г. Фрей выдвинул гипотезу, которую в 1986 г. доказал К. Рибет), что из доказательства проблемы Таниямы следует утверждение Великой теоремы Ферма. Однако, в начале декабря 1993 г., когда рукопись Э. Уайлса уже готова была отправиться в печать, в его доказательстве были обнаружены пробелы. Автор извинился и попросил 2 месяца для исправления. Только через год с небольшим появилось полное доказательство гипотезы Таниямы, но уже двух авторов – Э. Уайлса и Р. Тейлора. Пока специалисты новых пробелов в этой работе не нашли.
Сама по себе Великая теорема Ферма не имеет большого значения для математики. Однако она сыграла важную роль для развития теории алгебраических чисел, теории идеалов, алгебраической геометрии и математики в целом: попытки её доказательства приводили к открытию новых методов, обогативших многие смежные области математики.
Метод бесконечного спуска. Вот цитата из письма П. Ферма к Каркави от августа 1659 года: “Поскольку обычные методы, которые изложены в книгах, недостаточны для доказательства столь трудных предложений, я нашел совершенно особый путь для того, чтобы достичь этого. Я назвал этот способ доказательства бесконечным (infinie) или неопределенным (indefinie) спуском; в начале я пользовался им только для доказательства отрицательных предложений:
- что не существует числа, меньшего на единицу кратного трёх, которое составлялось бы из квадрата и утроенного квадрата;
- что не существует прямоугольного треугольника в числах, площадь которого была бы квадратным числом.
Доказательство проводится путём приведения к абсурду таким способом: если бы существовал какой-нибудь прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством.
Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы в силу подобного рассуждения третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности.
Но если задано число, то не существует бесконечности, по спуску меньших его (все время подразумеваются целые число). Откуда заключают, что не существует никакого прямоугольного треугольника с квадратной площадью”.
Этот метод бесконечного или неопределенного спуска действительно сделался одним из наиболее мощных средств диофантова анализа.
После П. Ферма его с успехом применяли Л. Эйлер и Л. Лагранж, а в наши дни – Л. Дж. Морделл, А. Вейль и другие. При этом метод был распространен на проблемы решения уравнения в рациональных числах. Осуществить метод спуска в общем случае теоремы Ферма мешает неединственность разложения целых чисел алгебраических колец в произведение простых сомножителей из того же кольца.
Проиллюстрируем суть метода бесконечного спуска простыми примерами.
Примеры: 1. Докажем, что 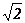 – иррациональное число.
– иррациональное число.
Предположим противное, т.е. что 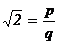 , где p, q Î N. Тогда имеем
, где p, q Î N. Тогда имеем 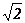 ×q = p, 2×q2 = p2, откуда видно, что p чётно: p = 2×p1 (p1 Î Z). Поэтому q2 = 2×p12, и теперь q чётно: q = 2×q1 (q1 Î Z). Кроме того,
×q = p, 2×q2 = p2, откуда видно, что p чётно: p = 2×p1 (p1 Î Z). Поэтому q2 = 2×p12, и теперь q чётно: q = 2×q1 (q1 Î Z). Кроме того, 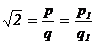 . Таким образом, начав с пары таких натуральных чисел (p; q), что
. Таким образом, начав с пары таких натуральных чисел (p; q), что 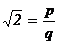 , получили новую пару натуральных чисел (p1; q1), где p1 < p, q1 < q, с тем же свойством. Точно так же по этой паре найдём пару (p2; q2), где p2 < p1, q2 < q1, и этот процесс построения новых пар можно продолжать бесконечно. Однако убывающая цепочка натуральных чисел p > p1 > p2 > … бесконечной быть не может. Полученное противоречие доказывает, что предположение о рациональности числа
, получили новую пару натуральных чисел (p1; q1), где p1 < p, q1 < q, с тем же свойством. Точно так же по этой паре найдём пару (p2; q2), где p2 < p1, q2 < q1, и этот процесс построения новых пар можно продолжать бесконечно. Однако убывающая цепочка натуральных чисел p > p1 > p2 > … бесконечной быть не может. Полученное противоречие доказывает, что предположение о рациональности числа 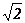 было неверно.
было неверно.
Докажем, что диофантово уравнение x2 + y2 = 3×z2 имеет только тривиальное решение x = y = z = 0.
Предположим, вопреки доказываемому, что (x; y; z) – нетривиальное решение. Тогда x и y делятся на 3. Действительно, рассматривая уравнение по модулю 3, получим сравнение x2 + y2 º 0 (mod 3), которое выполнено только при x º 0 º y (mod 3), в чём легко убедиться, перебрав возможные значения x, y Î {0, 1, 2}.
Теперь x = 3×x1, y = 3×y1 и 3×(x12 + y12) = z2, значит, z = 3×z1. Поэтому x12 + y12 = 3×z12. Таким образом, начиная с нетривиального решения (x; y; z), получили новое нетривиальное решение (x1; y1; z1 ), причём |x1| < |x|, |y1| < |y|, |z1| < |z|. По этому решению можно построить новое нетривиальное решение (x2; y2; z2 ), где |x2| < |x1|, |y2| < |y1|, |z2| < |z1 |, и этот процесс можно продолжать бесконечно. Однако убывающая цепочка натуральных чисел |x| > |x1| > |x2| > … не может быть бесконечной. Полученное противоречие показывает, что предположение о существовании нетривиального решения уравнения x2 + y2 = 3×z2 было неверным.
Проблема Ферма для показателя n = 4. Дадим короткое доказательство, использующее классификацию пифагоровых троек.
Теорема (о диофантовом уравнении x4 + y4 = z2). Диофантово уравнение x4 + y4 = z2 не имеет решений в натуральных числах. В частности, не имеет решений в натуральных числах и уравнение x4 + y4 = z4.
Доказательство. Пусть (x; y; z) – натуральное решение, т.е. x, y, z Î N. Если D = НОД(x, y) > 1, то для любого простого числа p, входящего в каноническое разложение D, число p4 входит в разложение z2, а значит, p2 входит в разложение z. Поэтому равенство x4 + y4 = z2 можно последовательно сокращать на p4, не нарушая вида этого равенства. Таким образом, через несколько шагов придём к аналогичному соотношению со взаимно простыми числами x, y.
Если НОД(x, y) = 1, то НОД(x, z) = 1 = НОД(y, z). Действительно, если, например, x и z делятся на некоторое простое число, то на это число делится и y4, а значит, y вопреки условию НОД(x, y) = 1. Таким образом, можно считать, что (x; y; z) – примитивное решение уравнения, т.е. все числа x, y, z попарно взаимно просты.
Если (x; y; z) –примитивное решение диофантова уравнения x4 + y4 = z2 в натуральных числах, то (x2; y2; z) – пифагорова тройка. Следовательно, она имеет один из следующих видов:
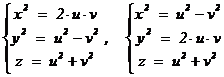 ,
,
где u, v – взаимно простые целые числа разной чётности.
Рассмотрим только первую возможность, когда y нечётно, т.к. во втором случае всё аналогично. Тогда y2 + v2 = u2, т.е. (y; v; u) – тоже пифагорова тройка, причём примитивная, т.к. u, v взаимно простые числа. Значит, y = s2 – t2, v = 2×s×t, u = s2 + t2 для некоторых взаимно простых натуральных чисел s, t. Поэтому из x2 = 4×s×t×(s2 + t2) следует x = 2×x 1 и x12 = s×t×(s2 + t2), причём числа s×t и s2 + t2 взаимно просты: если простое число p – их общий делитель, то p | s или p | t и p | (s2 + t2), откуда по свойствам делимости p – общий делитель взаимно простых чисел s, t, что невозможно. Следовательно, по следствию из основной теоремы арифметики, s2 + t2 = b2, s×t = a2, и далее s = m2, t = n2 и m4 + n4 = b2. Таким образом, по примитивному решению (x; y; z) построено новое примитивное решение (m; n; b), причём b < x12 < z, т.е. реализован метод бесконечного спуска.
Значит, диофантово уравнение x4 + y4 = z2 не имеет нетривиальных решений, а значит, их не имеет и уравнение x4 + y4 = z4.
Теорема доказана.
ЗАКЛЮЧЕНИЕ
Таким образом, я считаю что поставленная нами цель достигнута и мы можем решить некоторые диофантовы уравнения.
Систематическое изучение диофантовых уравнений („Диофантов анализ") требует от читателя весьма серьезной подготовки в области теории чисел. Такой элементарный диофантов анализ, выражаясь словами. Л. Эйлера, „немало служит к изощрению разума начинающих и большое проворство в исчислении приносит". Воспитательное значение его бесспорно. Задачи из этой области обычно требуют от читателя большой изобретательности и способствуют приобретению навыков самостоятельной работы в математике.
Следует заметить, что вообще диофантов анализ имеет большое теоретическое значение, поскольку многие его задачи тесно связаны с важнейшими вопросами теории чисел, а в последнее время он получает и прикладное значение, поскольку некоторые проблемы физики и механики приводят к диофантовым уравнениям.
Список литературы
1. Бухштаб А.А. Теория чисел [ Текст] / А.А. Бухштаб. – М., 1966.
2. Дэвенпорт Г. Высшая арифметика [ Текст] / Г. Дэвенпорт. – М., 1965.
3. Математическая энциклопедия [ Текст]: в 5 т. / гл. ред. И.М. Виноградов. М., 1977 - 1985.
4. Серпинский В. О решении уравнений в целых числах [ Текст] / В. Серпинский]/ – M., 1961.