Вероятностью события A называется отношение числа исходов m, благоприятствующих наступлению данного события  к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
 – вероятность случайного события
– вероятность случайного события
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 0≤P(A)≤1
Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1
Теоремы сложения вероятностей.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B);
P( +
+ 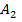 +…+
+…+  =P(
=P( +P
+P  +…+P(
+…+P( ).
).
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B)-P(AB)
Для трех совместных событий имеет место формула:
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Событие, противоположное событию A (т.е. ненаступление события A), обозначают  . Сумма вероятностей двух противоположных событий равна единице: P(A)+P(
. Сумма вероятностей двух противоположных событий равна единице: P(A)+P( )=1
)=1
Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью события A при условии B и обозначается 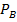 (A) или P(A/B).
(A) или P(A/B).
Если A и B – независимые события, то P(B)-  (B)=
(B)=  (B).
(B).
События A,B,C,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.
Теоремы умножения вероятностей.
Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(AB)=P(A)•P(B)
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле:
P(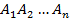 )=P(
)=P( )•P(
)•P(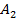 )… P(
)… P( ).
).
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
P(AB)=P(A)• 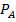 (B)=P(B)•
(B)=P(B)• 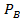 (A)
(A)
Разбор задач:
Задача 1.
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение: Событие A-билет выигрышный. Общее число различных исходов есть n=1000
Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле P(A)=  , получим P(A)=
, получим P(A)=  =
=  = 0,2
= 0,2
Задача 2.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение: Событие A-появление черного шара. Общее число случаев n=5+3=8
Число случаев m, благоприятствующих появлению события A, равно 3
P(A)=  =
=  = 0,375
= 0,375
Задача 3.
Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Решение: Событие A- появление двух черных шаров. Общее число возможных случаев n равно числу сочетаний из 20 элементов (12+8) по 2
n=  =
=  = 190
= 190
Число случаев m, благоприятствующих событию A, составляет
n=  =
= 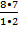 = 28
= 28
P(A)=  =
=  =
=  = 0,147
= 0,147
Задача 4.
В ящике в случайном порядке разложены 20 деталей, причем 5 из них стандартные. Рабочий берет наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной.
Задача 5.
Найти вероятность того, что наудачу взятое двухзначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно
Задача 6.
В одной урне находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение: Пусть A - появление белого шара из первой урны, а B – появление белого шара из второй урны. Очевидно, что события A и B независимы. Найдем P(A)=4/12=1/3, P(B)=3/12=1/4, получим
P(AB)=P(A)•P(B)=(1/3)•(1/4)=1/12=0,083
Задача 7.
В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными.
Решение: Введем следующие обозначения: A – первая взятая деталь стандартная; B – вторая взятая деталь стандартная. Вероятность того, что первая деталь стандартная, составляет P(A)=8/12=2/3. Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартной первая деталь, т.е. условная вероятность события B, равна 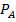 (B)=7/11.
(B)=7/11.
Вероятность того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
P(AB)=P(A)•  (B)=(2/3)•(7/11)=14/33=0,424
(B)=(2/3)•(7/11)=14/33=0,424