Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.
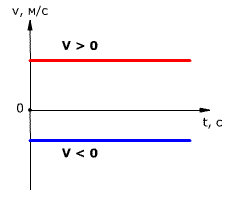
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
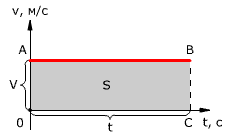
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна
v = s1 / t1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
tg α = v
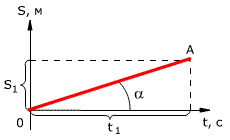
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
tg α1 > tg α2
следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2).
tg α3 = v3 < 0
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
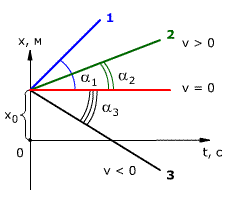
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Связь угловых и линейных величин
Отдельные точки вращающегося тела имеют различные линейные скорости 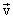 . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости
. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 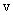 определяется скоростью вращения тела
определяется скоростью вращения тела 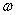 и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени
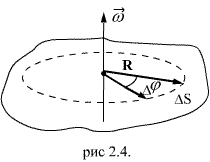
и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени 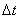 тело повернулось на угол
тело повернулось на угол 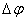 (рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный
(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный
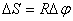
Линейная скорость точки по определению.
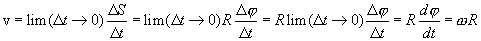
| (2.6) |
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:
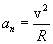
подставляя значение скорости из (2.6), находим:
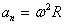
| (2.7) |
Тангенциальное ускорение
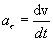
Воспользовавшись тем же отношением (2.6) получаем
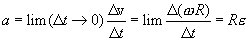
| (2.8) |
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.
Основные понятия.
Периодическим колебанием называется процесс, при котором система (например, механическая) возвращается в одно и то же состояние через определенный промежуток времени. Этот промежуток времени называется периодом колебаний.
Возвращающая сила - сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.
В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.
Свободные колебания имеют место тогда, когда на колеблющееся тело действует только возвращающая сила. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).
Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которую называют вынуждающей. Во многих случаях системы совершают колебания, которые можно считать гармоническими.
Гармоническими колебаниями называют такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса:
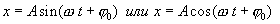
| (7.1) |
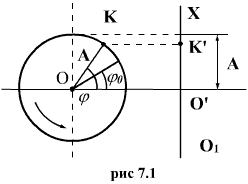
Для иллюстрации физического смысла 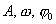 рассмотрим окружность, и будем вращать радиус ОК с угловой скоростью ω против часовой (7.1) стрелки. Если в начальный момент времени ОК лежал в горизонтальной плоскости, то через время t он сместится на угол
рассмотрим окружность, и будем вращать радиус ОК с угловой скоростью ω против часовой (7.1) стрелки. Если в начальный момент времени ОК лежал в горизонтальной плоскости, то через время t он сместится на угол 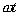 . Если начальный угол отличен от нуля и равен φ0, тогда угол поворота будет равен
. Если начальный угол отличен от нуля и равен φ0, тогда угол поворота будет равен 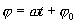 Проекция
Проекция 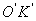 на ось ХО1 равна
на ось ХО1 равна 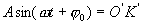 . По мере вращения радиуса ОК изменяется величина проекции, и точка
. По мере вращения радиуса ОК изменяется величина проекции, и точка 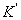 будет совершать колебания относительно точки
будет совершать колебания относительно точки 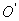 - вверх, вниз и т.д. При этом максимальное значение х равно А и называется амплитудой колебаний; ω - круговая или циклическая частота;
- вверх, вниз и т.д. При этом максимальное значение х равно А и называется амплитудой колебаний; ω - круговая или циклическая частота; 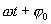 - фаза колебаний;
- фаза колебаний; 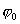 – начальная фаза. За один оборот точки К по окружности ее проекция совершит одно полное колебание и вернется в исходную точку.
– начальная фаза. За один оборот точки К по окружности ее проекция совершит одно полное колебание и вернется в исходную точку.
Периодом Т называется время одного полного колебания. По истечению времени Т повторяются значения всех физических величин, характеризующих колебания. За один период колеблющаяся точка проходит путь, численно равный четырем амплитудам.
Угловая скорость определяется из условия, что за период Т радиус ОК сделает один оборот, т.е. повернется на угол 2π радиан:
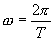 или
или 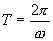
Частота колебаний - число колебаний точки в одну секунду, т.е. частота колебаний определяется как величина, обратная периоду колебаний:
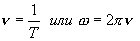
Пружынный маятник упругие силы.
Пружинный маятник состоит из пружины и массивного шара, насаженного на горизонтальный стержень, вдоль которого он может скользить. Пусть на пружине укреплен шарик с отверстием, который скользит вдоль направляющей оси (стержня). На рис. 7.2,а показано положение шара в состоянии покоя; на рис. 7.2,б - максимальное сжатие и на рис. 7.2,в -произвольное положение шарика.
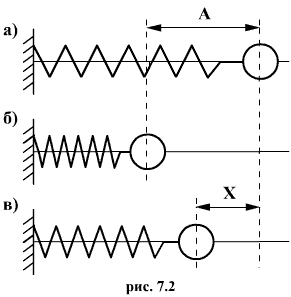
Под действием возвращающей силы, равной силе сжатия, шарик будет совершать колебания. Сила сжатия F = -kx, где k - коэффициент жесткости пружины. Знак минус показывает, что направление силы F и смещение х противоположны. Потенциальная энергия сжатой пружины
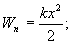 кинетическая
кинетическая 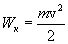 .
.
Для вывода уравнения движения шарика необходимо связать х и t. Вывод основывается на законе сохранения энергии. Полная механическая энергия равна сумме кинетической и потенциальной энергии системы. В данном случае:
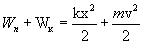 .
.
В положении б) 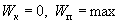 :
:
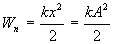 .
.
Так как в рассматриваемом движении выполняется закон сохранения механической энергии, можно записать:
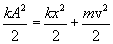 .
.
Определим отсюда скорость:
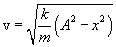
Но в свою очередь 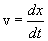 и, следовательно,
и, следовательно,
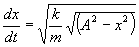 .
.
Разделим переменные
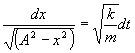 .
.
Интегрируя это выражение, получим:
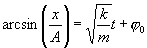 ,
,
где 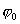 - постоянная интегрирования.
- постоянная интегрирования.
Из последнего следует, что
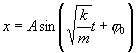
| (7.2) |
Сравнивая (7.1) с (7.2), получаем
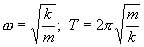
| (7.3) |
Таким образом, под действием упругой силы тело совершает гармонические колебания. Силы иной природы, чем упругие, но в которых выполняется условие F = -kx, называются квазиупругими. Под действием этих сил тела тоже совершают гармонические колебания. При этом:
| смещение: | 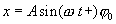
|
| скорость: | 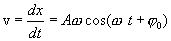
|
| ускорение: | 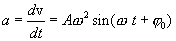
|
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
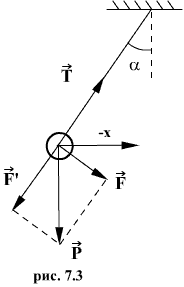
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 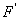 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 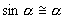 и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
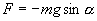
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
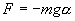
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 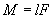 , и момент инерции:
, и момент инерции:
M = FL.
Момент инерции J в данном случае
Угловое ускорение:
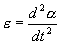
С учетом этих величин имеем:
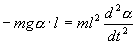
или
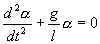
| (7.8) |
Его решение
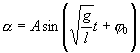 ,
,
где 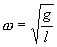 и и 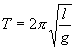
| (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Затухающие колебания.
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.
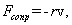
| (7.17) |
где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 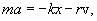
или
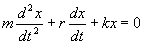
| (7.18) |
Перепишем это уравнение в следующем виде: 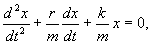
и обозначим: 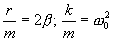
где 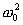 представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда
представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда
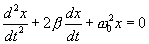
| (7.19) |
Будем искать решение уравнения (7.19) в виде
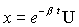
где U - некоторая функция от t.
Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 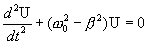
Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение 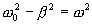 тогда С вещественным ω решением этого уравнения, как мы знаем, является функция
тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 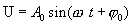
Таким образом, в случае малого сопротивления среды 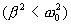 , решением уравнения (7.19) будет функция
, решением уравнения (7.19) будет функция
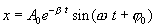
| (7.20) |
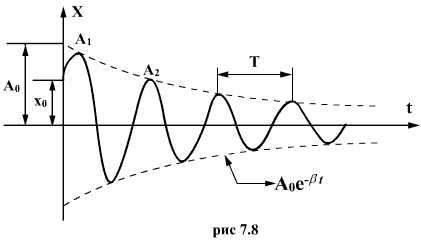
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину 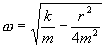 называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину
называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину 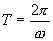 обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.
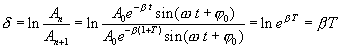
Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда
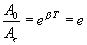
откуда
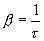
Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.
Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда
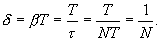
Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз
Вынужденные колебания.
В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы периодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы 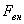 .
.
Пусть эта сила изменяется со временем по закону 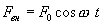 , где
, где 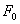 амплитуда вынуждающей силы
амплитуда вынуждающей силы 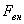 . Возвращающая сила
. Возвращающая сила 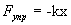 и сила сопротивления
и сила сопротивления 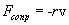 Тогда второй закон Ньютона можно записать в следующем виде:
Тогда второй закон Ньютона можно записать в следующем виде:
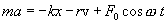
или
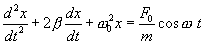
| (7.21) |
Предположим, что возникающее под действием силы установившиеся вынужденные колебания системы также являются гармоническими: 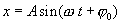 (7.22) причем их циклическая частота равна циклической частоте ω вынуждающей силы.
(7.22) причем их циклическая частота равна циклической частоте ω вынуждающей силы.
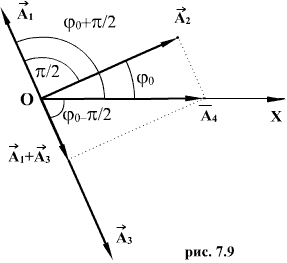
Дифференцируя два раза (7.22) и подставляя в (7.21), получим
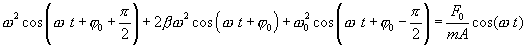
Обозначим: 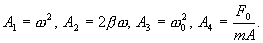
Тогда последнее равенство можно записать в следующем виде:
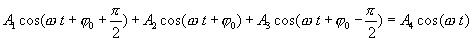
Правую часть этого выражения можно рассматривать как уравнение некоторого гармонического колебания, получившегося при сложении трех гармонических колебаний, определяемых слагаемыми левой части этого равенства. Для сложения этих колебаний воспользуемся методом векторных диаграмм. Проведем опорную линию ОХ (рис. 1.9) и отложим под углами, соответствующими начальным фазам всех четырех колебаний векторы 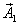 ,
, 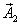 ,
, 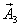 ,
, 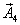 их амплитуды таким образом, чтобы
их амплитуды таким образом, чтобы
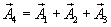
Из рис. 7.9 видно, что 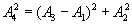 Подставляя в последнее значения соответствующих амплитуд (1.22), получим:
Подставляя в последнее значения соответствующих амплитуд (1.22), получим:
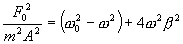
отсюда
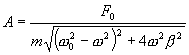
| (7.23) |
Амплитуда установившихся вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F0, обратно пропорциональна массе m системы и уменьшается с увеличением коэффициента затухания β. При постоянных F0, m и β амплитуда зависит только от соотношения циклических частот вынуждающей силы β и свободных незатухающих колебаний системы 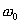 . При циклической частоте вынуждающей силы ω=0 амплитуда колебаний
. При циклической частоте вынуждающей силы ω=0 амплитуда колебаний 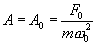 . В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F0:
. В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F0:
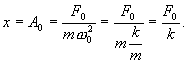
Поэтому отклонение A0 иногда называют статической амплитудой.
Если нет диссипации т.е β=0, то амплитуда колебаний
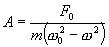
растет с увеличением циклической частоты ω вынуждающей силы Fвн и при 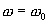 становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем
становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем
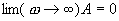
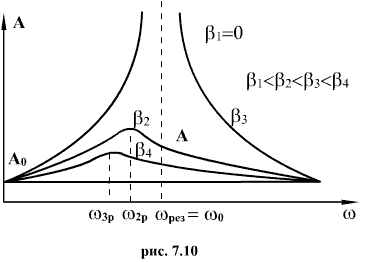
Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы 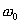 называется резонансом.
называется резонансом.
Если затухание существует 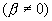 то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого
то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого 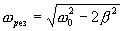 , где
, где 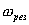 - называют резонансной частотой.
- называют резонансной частотой. 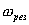 обозначает то значение циклической частоты ω вынуждающей силы, при котором
обозначает то значение циклической частоты ω вынуждающей силы, при котором 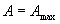 .
.
Из последней формулы следует, что для консервативной системы 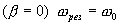 , а для диссипативной системы
, а для диссипативной системы 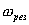 несколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец при
несколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец при 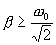 исчезает совсем.
исчезает совсем.
Явление резонанса используется для усиления колебаний, например, электромагнитных. Однако при конструировании различных машин и сооружений необходимо учитывать даже самую небольшую периодическую силу с тем, чтобы предотвратить нежелательные последствия резонанса.
Стоячие волны
Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны
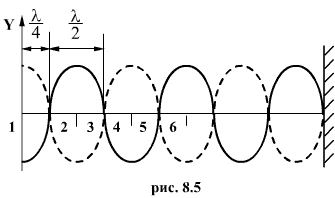
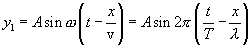
и уравнения отраженной волны
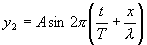
Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме 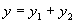 . После несложных преобразований, получаем
. После несложных преобразований, получаем
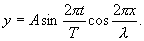
| (8.15) |
Это уравнение стоячей волны определяет смещение любой точки волны.
Величина 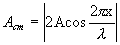
| (8.16) |
не зависит от времени и определяет амплитуду любой точки с координатой х. Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда Аст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния х. Если придавать х значения, равные 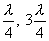 и т.д., то при подстановке в уравнение (8.16) получим
и т.д., то при подстановке в уравнение (8.16) получим 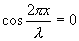 . Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
. Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
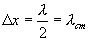
где λ - длина бегущей волны.
В стоячей волне все точки среды, в которой они распространяются, расположенные между двумя соседними узлами, колеблются в одной фазе. Точки среды, лежащие по разные стороны от узла, колеблются в противофазе -фазы их отличаются на π. т.е. при переходе через узел фаза колебаний скачкообразно меняется на π. В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная волны переносят энергию в равных количествах и в прямом и в противоположном направлениях. В том случае, когда волна отражается от среды более плотной, чем та среда, где распространяется волна, в месте отражения возникает узел, фаза изменяется на противоположную. При этом говорят, что происходит потеря половины волны. Когда волна отражается от среды менее плотной в месте отражения, появляется кучность, и потери половины волны нет.
Термодинамическое состояние тела (например, газа) характеризуется его массой 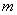 , молярной массой μ, давлением
, молярной массой μ, давлением 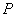 , объемом
, объемом 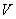 , температурой
, температурой 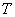 (а возможно, и другими величинами, например, определяющими его химический состав). Все эти величины называются термодинамическими параметрами тела. Однако, как будет видно из дальнейшего, такие параметры, как
(а возможно, и другими величинами, например, определяющими его химический состав). Все эти величины называются термодинамическими параметрами тела. Однако, как будет видно из дальнейшего, такие параметры, как 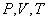 ,имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия (т.д.р.). Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными (к этому следует добавить еще условие отсутствия стационарных потоков). Если, например, быстро подогревать газ, как это показано на рис. 9.1, температура непосредственно подогреваемой части сосуда А окажется выше температуры части В. Не будут равны и давления в частях А и В. В этом случае не имеет смысла понятие температуры
,имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия (т.д.р.). Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными (к этому следует добавить еще условие отсутствия стационарных потоков). Если, например, быстро подогревать газ, как это показано на рис. 9.1, температура непосредственно подогреваемой части сосуда А окажется выше температуры части В. Не будут равны и давления в частях А и В. В этом случае не имеет смысла понятие температуры 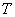 или давления
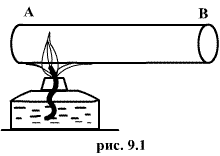
или давления 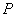 всего газа. Другой пример – впустим в газ пучок быстрых молекул. Ясно, что не имеет смысла говорить о температуре газа до тех пор, пока быстрые молекулы, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние т.д.р.
всего газа. Другой пример – впустим в газ пучок быстрых молекул. Ясно, что не имеет смысла говорить о температуре газа до тех пор, пока быстрые молекулы, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние т.д.р.
В состоянии т.д.р. для каждого вещества термодинамические параметры связаны между собой так называемым уравнением состояния:
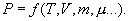
| (9.1) |
Таким уравнением состояния для идеального газа является уравнение Менделеева – Клапейрона:
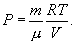
| (9.2) |
Здесь R=8,31 Дж/(мольК) – универсальная газовая постоянная, μ - молярная масса. Для углерода (С) величина μ составляет 12г, для водорода (H2) – 2г, для кислорода (О2) – 32г, для воды (Н2О) – 18г и т.д.
В моле любого вещества содержится одно и то же количество молекул N0, называемое числом Авогадро:
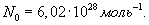
| (9.3) |
Это объясняется тем, что значение моля любого вещества выбрано пропорциональным массе молекулы этого вещества. Масса молекулы может быть получена делением массы моля на число Авогадро:
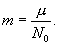
| (9.4) |
Отношение универсальной газовой постоянной R к числу Авогадро (т.е. универсальная газовая постоянная, приходящаяся на одну молекулу) называется постоянной Больцмана:
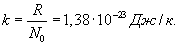
| (9.5) |
В формулу (9.2) входят еще давление, объем, температура и масса газа. Давление Р в системе СИ измеряется в ньютонах на квадратный метр или паскалях (Н/м2=Па), объем V – в кубических метрах (м2), масса m – в килограммах (кг), температура T – в кельвинах (К). Абсолютная температура Т отсчитывается от абсолютного нуля (-273,15°С), т.е. Т=t+273,15, где t – температура по Цельсию.
Если количество вещества равно 1 молю, то (9.2) превращается в
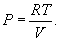
| (9.6) |
Идеальным газом называется газ, настолько разреженный, что он подчиняется уравнению (9.2) или(9.6). Смысл этого определения состоит, очевидно, в том, что для подчинения уравнению (9.6) газ должен быть достаточно разреженным. Если газ, напротив, сжат до достаточно больших плотностей (так называемый реальный газ), то вместо (9.6) имеем
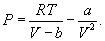
| (9.7) |
Это – уравнение состояния реального газа или уравнение Ван-дер-Ваальса. Здесь a и b – постоянные.
Внутр Энергия Ид газа
Под внутренней энергией (U) понимается вся энергия системы (тела) за исключением механической энергии системы как целого. Что именно входит во внутреннюю энергию системы? Сюда входит кинетическая энергия поступательного движения ее молекул, потенциальная энергия их взаимодействия между собой, энергия возбуждения колебаний и вращений молекул. Здесь перечислены лишь те виды энергии системы, которые могут меняться в рассматриваемых нами термодинамических процессах. Например, энергию возбуждения атомных ядер нужно будет включить, если будут рассматриваться температуры, при которых такое возбуждение может произойти.
Поскольку состояние термодинамической системы (например, газа) определяется величинами m, μ, V, T (давление P само определяется этими же величинами), то от них должна зависеть и внутренняя энергия U. Опустим пока постоянные для данного тела m и μ (ниже примем их во внимание), запишем U=U(V,T). Зависимость внутренней энергии от объема V связана с тем, что при изменении объема меняется расстояние между молекулами и, следовательно, потенциальная энергия их взаимодействия. Эта зависимость существенна только для реального газа. Для идеального газа внутренняя энергия должна зависеть только от температуры, т.е. U=U(T), так как температура определяет среднюю кинетическую энергию молекул.
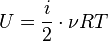 ,
,
Работа газа
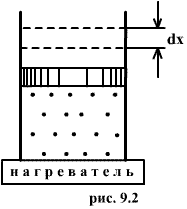
Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 9.2). Отметим, что слово «газ» здесь совершенно условно. Это может быть жидкость, кристалл и вообще любое тело. Цилиндр контактирует с нагревателем или холодильником, который может сообщать газу тепло или отбирать его.
Пусть на поршень оказывается внешнее давление, величина которого может быть любой.
Все процессы, которые будем рассматривать ниже, будут квазистатическими, т.е. медленными настолько, чтобы можно было считать, что в каждый момент газ находится в состоянии т.д.р. Если очень быстро сжать газ, то давление его у поршня окажется на какой-то момент больше, чем в стальном объеме, и тогда нельзя будет говорить о давлении газа вообще. Такой процесс не является квазистатическим. Приближенно квазистатическими являются и процессы, достаточно быстрые с технической точки зрения, например процессы, происходящих в цилиндрах двигателя автомашины во время работы мотора (оказывается, для приближенной квазистатичности требуется, чтобы скорость поршня была мала по сравнению со скоростью звука в газе).
Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень на рис.9.2 поднимается на величину dx. Тогда газ выполнит работу 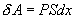 (S – площадь поршня). Получим
(S – площадь поршня). Получим
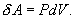
| (9.8) |
Эта величина называется элементарной работой газа. Работа при расширении газа от объема V1 до V2 будет равна
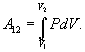
| (9.9) |
Если по одной оси отложить объем газа, по другой – его давление (плоскость P – V), то работа (9.9) будет изображаться площадью под кривой P(V) (рис.9.3).
Процесс расширения от объема V1 до объема V2 может происходить различным образом: например, можно при этом изолировать газ от нагревателя или, наоборот, нагревать газ и т.д. Иначе говоря, при перемещении из точки 1 в точку 2 в газе могут происходить различные процессы, даже если зафиксировано начальное и конечное состояния. В каждом процессе работа будет иметь свое значение, так как площадь под кривой процесса будет различной (кривые I, II, и III на рис.9.3). Таким образом, выполняемая газом работа зависит от процесса, который с ним происходит. Обычно (хотя это и не совсем точное выражение) говорят, что «работа газа есть функция процесса».
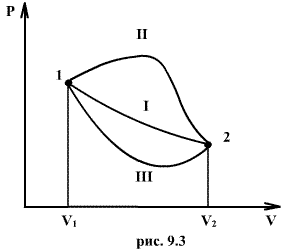
Заметим, что работа положительна, если она выполняется газом, и отрицательна, если внешние силы выполняют ее над газом.
Тепло ёмкость
В термодинамике для характеристики тепловых свойств тел используется понятие теплоемкости.
Теплоемкость - количество теплоты необходимое для нагревания тела на один Кельвин
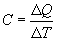
| (9.11) |
Удельной теплоемкостью называется величина, числено равная теплоте, которую надо сообщить единице массы тела для повышения его температуры на один Кельвин:
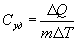
| (9.12) |
Отсюда можно определить количество теплоты, необходимое для нагревания вещества, массы m
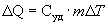
| (9.13) |
Молярная теплоемкость - количество тепла необходимое для нагревания одного моля вещества на один Кельвин
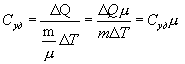
| (9.14) |
Воспользовавшись I законом термодинамики выражение (9.11) можно переписать в виде
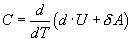
| (9.15) |
откуда следует, что теплоемкость есть функция процесса, т.е. теплоемкость системы зависит от того каким образом система переходит из одного состояния в другое. Вообще говоря, таких процессов может быть сколько угодно, фактически же используются чаще всего теплоемкость при р=const(Cp) и при V=const(CV).