Тема 2.Силы - действующие на жидкость.
Гидростатическое давление и его параметры.
Дифференциальное уравнение жидкости в состоянии покоя. Интегрирование основного уравнения гидростатики.
Распределительная эпюра гидростатического давления. Центр давления. Силы давления, действующие на горизонтальную и криволинейную стенку. Относительное равновесие жидкостей.
Приборы - измеряющие давление.
Силы - действующие на жидкость. Жидкость подвержена действию двух категорий внешних сил: объёмных (массовых) и поверхностных. Объёмными называются силы, пропорциональные объёму жидкости (силы тяжести и силы инерции), поверхностными - силы, приложенные к поверхности, ограничивающей объём жидкости, или к поверхности, проведённой внутри этого объёма.
В общем случае (при равномерном распределении этих сил по поверхности) величина поверхностной силы пропорциональна площади, на которую она действует.
В качестве примера поверхностной силы можно привести атмосферное давление, действующее на поверхность жидкости, помещённой в открытом сосуде.
Гидростатическое давление и его параметры. Гидростатикой - называют раздел гидравлики, в котором рассматриваются законы равновесия жидкостей и практические приложения этих законов.
Выделим в жидкости, находящейся в равновесии, некоторый объём, (рис.2.1) рассечём его произвольной плоскостью АВ на две части и мысленно
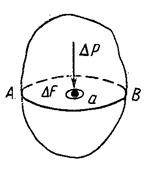
Рис.2.1
отбросим одну из них, верхнюю. При этом к плоскости АВ мы должны приложить силы, действие которых будет эквивалентно действию отброшенной верхней части объёма на оставшуюся нижнюю его часть.
Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку а. Пусть эту площадь из названных сил взаимодействия приходится сила ΔP. Отношение 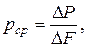 представляющее собой силу, действующую на единицу площади, будем называть среднимгидростатическим давлением, или средним напряжением гидростатического давления по площади ΔF.
представляющее собой силу, действующую на единицу площади, будем называть среднимгидростатическим давлением, или средним напряжением гидростатического давления по площади ΔF.
Истинное давление в различных точках этой площади может быть разным; в одних точках оно больше, а в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление
рср будет тем меньше отличаться от истинного в точке а, чем меньшей будет площадь ΔF, и в пределе (при стремлении её к нулю) среднее гидростатическое давление совпадает в этой точке с истинным.
Таким образом, истинное гидростатическое давление р (обычно называемое просто гидростатическим) будет 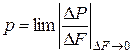 .
.
Для жидкостей, находящихся в равновесии, оно аналогично напряжению сжатия в твёрдых телах.
На практике гидростатическое давление определяют различными способами. Если при этом учитывают атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным.
Часто атмосферное давление на свободную поверхность не принимают во внимание, определяя так называемое избыточное, или манометрическое (сверх атмосферного), давление. Манометрическое давление есть разность между абсолютным давлением в жидкости и атмосферным давлением:
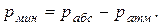
Встречаются случаи, когда гидростатическое давление в жидкости оказывается меньше атмосферного. В таких случаях говорят о вакууме (разряжении). Вакуум определяется разностью между атмосферным, и абсолютным давлением в жидкости (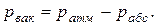 ) и изменяется в пределах от нуля до 0,01МПа.
) и изменяется в пределах от нуля до 0,01МПа.
Вакуум можно также характеризовать абсолютным давлением.
Гидростатическое давление обладает следующими двумя основными свойствами: оно направлено по внутренней нормали к площадке, на которую действует, и его значение в данной точке не зависит от направления (т.е. от ориентировки в пространстве площадки, включающей эту точку).
Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.
Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на нормальную и касательную составляющие. Наличие последней ввиду отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению вдоль площадки, т.е. нарушило бы её равновесие. Следовательно, единственно возможным направлением гидростатического давления является его направление по нормали к площадке.
Предположим далее, гидростатическое давление будет направлено по внешней, а не по внутренней нормали, т.е. не внутрь рассматриваемого объёма, а наружу. Так как жидкость не оказывает сопротивления растягивающим усилиям, то и в этом случае частицы жидкости придут в движение, и её равновесие будет нарушено. Значит, гидростатическое давление всегда направлено по внутренней нормали и представляет собой сжимающее давление.
Для доказательства второго свойства выделим в покоящейся жидкости призму (рис.2.2) сечением ΔF. Один торец призмы пусть будет перпендикулярен к образующей, а второй – наклонён к ней пол углом α. Длину призмы обозначим L. Мысленно отбросив жидкость, окружающую выделенную в ней призму, заменим действие отброшенной жидкости силами давления на грани призмы. В соответствии со сказанным выше, это будут силы, нормальные к граням.
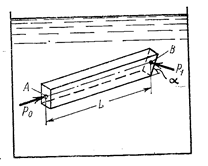
Рис.2.2
Обозначим далее через ро и р1 среднее давление соответственно на торце, перпендикулярном к образующей, и на скощенном торце; составим выражение для суммы проекций всех сил, действующих на призму и на ось, совпадающую с осью призмы. Поскольку призма находится в равновесии, указанная сумма проекций сил должна равняться нулю. Пусть Q – проекция на эту ось единичной объёмной силы, т.е. силы, приложенной к единице объёма (в частном случае, когда из объёмных сил действует только сила тяжести, 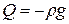 ). Тогда проекция объёмных сил, приложенных к призме будет
). Тогда проекция объёмных сил, приложенных к призме будет 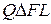 ;
;
проекция силы давления на торец А 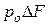 , а силы давления на скошенный торец -
, а силы давления на скошенный торец - 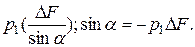
Силы давления на боковые грани призмы проекций на её ось не дадут. Поэтому сумма проекций всех сил составит 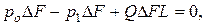 откуда
откуда 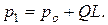 (*).
(*).
Следовательно, величина р1 оказывается не зависящей от угла α. В пределе (при ΔF, стремящемся к нулю) ро и р1 представляют собой истинные значения давления в точках А и В и в соответствии с уравнением (*) определяются положением этих точек в пространстве. Таким образом, гидростатическое давление во всякой точке имеет одно и тоже значение по всем направлениям и является функцией только её координат: 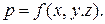
Из уравнения (*) следует также, что если давление, например в точке А изменится на величину Δ ро, то на такую же величину изменится оно и в любой точке жидкости. В этом заключается известный из физики закон Паскаля, формулируемый обычно следующим образом: давление, производимое на жидкость, передаётся внутри жидкости во все стороны с одинаковой силой.
Дифференциальное уравнение жидкости в состоянии покоя (уравнения Эйлера ). Выделим в жидкости, находящейся в покое, бесконечно малый объём в форме параллелепипеда со сторонами, параллельными осям координат и равными соответственно dx, dy, dz (рис.2.3), и рассмотрим равновесие действующих на этот параллелепипед внешних сил.
Такими силами являются: 1) поверхностные силы гидростатического давления на грани параллелепипеда со стороны окружающей его жидкости; 2) объёмные (массовые) силы.
Составим уравнения проекций этих сил на координатные оси. При этом ограничимся подробным рассмотрением лишь одного из них, например уравнения проекций на ось х. Обозначим через р гидростатическое давление в одной какой-либо точке грани abcd и будем считать его средним для всей

Рис.2.3.
грани. Тогда полная сила давления на эту грань с точностью до бесконечно малых высшего порядка определится выражением dPx = pdydz, где dydz – площадь грани.
Давление на противоположную грань a’b’c’d’ будет отличаться от этого давления. Здесь необходимо учесть, что гидростатическое давление в покоящейся жидкости зависит от координат и изменяется непрерывно по линейному закону. Поскольку при переходе от грани abcd к грани a’b’c’d’ изменилась только одна координата x (на величину dx), гидростатическое давление на этой грани будет 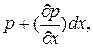 где
где 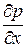 -частный дифференциал, взятый по координате x.
-частный дифференциал, взятый по координате x.
При этом полная сила давления на грань a’b’c’d’: 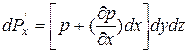
Указанные силы dPx и dP’x проектируется на ось x в натуральную величину. Направление первой из них совпадает с её положительным направлением, а вторая направлением, а вторая направлена в противоположную сторону.
Найдём далее проекцию объёмных (массовых) сил dQ на ось x. Определим её как произведение элементарной массы рассматриваемого параллелепипеда dm = ρdxdydz на проекцию ускорения этих X* сил на ту же ось: dQx = dmX = ρdxdydzX.
Просуммировав и приравняв к нулю установленные таким образом выражения для проекций всех действующих на рассматриваемый параллелепипед сил, получим первое уравнение равновесия:
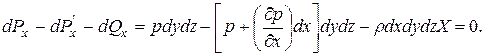
После ряда несложных преобразований найдём 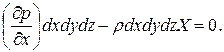 Разделив затем это уравнение на ρdxdydz (т.е. отнеся все силы к единицы массы), будем иметь:
Разделив затем это уравнение на ρdxdydz (т.е. отнеся все силы к единицы массы), будем иметь: 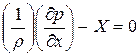 .
.
Аналогичные уравнения получим для проекций на оси y и z: 
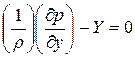 ,
, 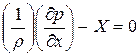 .
.
Эти уравнения можно представить также в виде 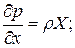
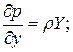
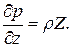 (**)
(**)
Их называют дифференциальными уравнениями жидкости. Впервые они были выведены в 1775 г. Л.Эйлером и выражают в дифференциальной форме закон распределения гидростатического давления.
Интегрирование основного уравнения гидростатики. Будем исходить издифференциальных уравнений равновесия (**).Умножим каждое из них соответственно на dx, dy, dz и сложим. Получим
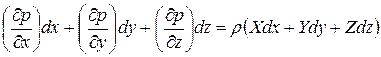 (***)
(***)
Так как в случае равновесия гидростатическое давление, является функцией только координат 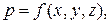 левая часть этого уравнения представляет собой полный дифференциал dp. Следовательно,
левая часть этого уравнения представляет собой полный дифференциал dp. Следовательно,
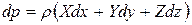 (а)
(а)
Соблюдение условий равновесия требует при этом, чтобы и правая часть уравнения (***) была полным дифференциалом некоторой другой функции U координат 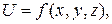 частные производные которой по координатам равны поекциям ускорений объёмных сил:
частные производные которой по координатам равны поекциям ускорений объёмных сил:
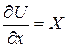 ;
; 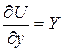 ;
; 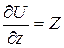 (б)
(б)
Такая функция называется силовой, или потенциальной, а силы, удовлетворяющие условиям (б), силами, имеющими потенциал.
Таким образом,
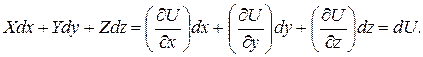 (в)
(в)
При этом уравнение (***) принимает вид
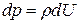 (****)
(****)
и может быть проинтегрировано.
Рассмотрим наиболее часто встречающийся на практике случай равновесия тяжелой (т.е.находящейся под воздействием одной только силы тяжести), однородной (ρ = const) капельной жидкости. При этом проекции ускорения объёмных сил будут равны: Х = 0; Y = 0; Z = -g, и уравнение (****) получит следующую форму записи: 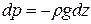 или, то же самое,
или, то же самое,
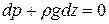 (****’)
(****’)
Проинтегрировав последнее уравнение, найдём:
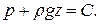 (*****)
(*****)
Постоянная интегрирования С может быть определена здесь, например, из условий на свободной поверхности жидкости. Обозначив через ро давление в какой-нибудь точке этой поверхности, а через zо её ординату, будем иметь:
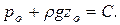
После подстановки последнего выражения в уравнение (*****) получим:
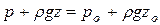 , или
, или
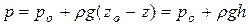 , (******)
, (******)
где h=zo – z – глубина погружения рассматриваемой точки под свободной поверхностью.
Уравнение (******) является фундаментальным. Оно называется, основным уравнением гидростатики показывает, что гидростатическое давление в любой точке покоящейся тяжёлой капельной жидкости полностью определяется глубиной её погружения под свободной поверхностью жидкости или под какой-либо другой поверхностью с известным на ней давлением, говоря иначе, изменяется в зависимости только от вертикальной координаты этой точки
Распределительная эпюра гидростатического давления. Изменения гидростатического давления на поверхность, ограничивающую жидкость, изображают очень наглядно при помощи графиков, или эпюр давления. При этом давление, возрастающее с глубиной погружения точки его приложения по линейному закону, откладывают в определённом масштабе в виде отрезков, нормальных к поверхности.
Предположим, требуется построить эпюру абсолютного давления на вертикальную стенку АВ сосуда, наполненную жидкостью, имеющей плотность ρ, до уровня h (рис.2.4 а). Давление на свободной поверхности жидкости равно атмосферному.
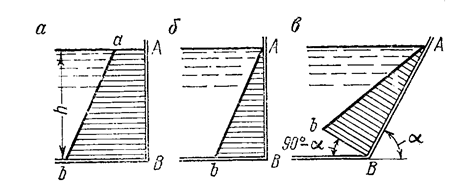
Рис.2.4
Изменение гидростатического давления по высоте стенки в этом случае определяется выражением 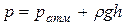 , представляющим уравнение прямой линии. Поэтому для построения эпюры давления необходимо отложить от точки А на свободной поверхности жидкости (h=0) отрезок аА соответствующий в масштабе построения атмосферному давлению, а от точки В у дна сосуда – отрезок hВ, соответствующий давлению в этой точке
, представляющим уравнение прямой линии. Поэтому для построения эпюры давления необходимо отложить от точки А на свободной поверхности жидкости (h=0) отрезок аА соответствующий в масштабе построения атмосферному давлению, а от точки В у дна сосуда – отрезок hВ, соответствующий давлению в этой точке 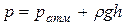 , и соединить концы этих отрезков прямой ав. Полученная фигура – трапеция АавВ и будет эпюрой гидростатического давления.
, и соединить концы этих отрезков прямой ав. Полученная фигура – трапеция АавВ и будет эпюрой гидростатического давления.
Эпюра избыточного (манометрического) давления 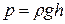 для этой же стенки, очевидно, будет иметь вид прямоугольного треугольника АвВ (рис.2.4.б).
для этой же стенки, очевидно, будет иметь вид прямоугольного треугольника АвВ (рис.2.4.б).
В том случае, когда сосуд имеет наклонную стенку, составляющую с горизонтальной плоскостью некоторый угол α, эпюра избыточного гидростатического давления представляет собой также отрезки, изображающие давление, наклонены к горизонтальной плоскости под углом 90о- α.
Если стенка состоит из ряда отдельных плоских граней, наклонённых под различными углами к горизонту (рис.2.5.а) в виде некоторой ломаной линии АВСД, эпюра гидростатического давления может быть построена так же, как и для обычной плоской стенки. Для этого отложим сначала от точки В нормально к грани АВ отрезок Вb, изображающий гидростатическое давление в этой точке.
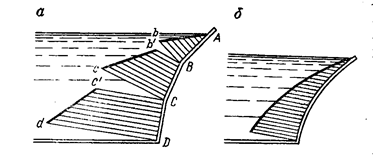
Рис.2.5
Затем соединим точки А и b п рямой и получим эпюру давления на указанную грань в виде прямоугольного треугольника АbВ. Затем перейдём к построению давления на грань ВС. Отложим от точек В и С этой грани нормально к ней отрезки, соответствующие гидростатическим давлениям: от точки В – отрезок Вв´, равный Вв, и от точки С – отрезок Сс. В результате получим трапецию Вв´ сС, представляющую собой эпюру давления на грань ВС.
Аналогичным путём построим эпюру давления и для последней СDd (трапеция Сс´dD).
Отметим также случай, когда стенка имеет криволинейную форму. Гидростатическое давление в отдельных точках такой стенки также изображается отрезками прямых, нормальных к стенке в соответствующих точках, а эпюра давления в этом случае представляет криволинейный треугольник (рис.2.5. б).
Центр силы давления действующий на горизонтальную стенку. Зная закон распределения гидростатического давления в жидкости, можно найти полную силу давления на ограничивающие жидкость поверхности – стенки и дно сосуда. Эта задача сводится к определению силы давления (по значению и направлению) и нахождению точки её приложения.
Рассмотрим сначала плоские поверхности – плоские стенки.
Предположим, что имеется плоская стенка площадью F, наклонённая к горизонту под некоторым углом α (рис.2.6). Разделим её по высоте на ряд элементарных горизонтальных весьма узких полосок dF и определим давление на одну из них.
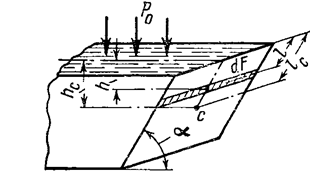
Рис.2.6
Гидростатическое давление в любой точке на оси полоски определяется 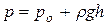 , где ро – давление на свободной поверхности жидкости; h – глубина погружения рассматриваемой точки.
, где ро – давление на свободной поверхности жидкости; h – глубина погружения рассматриваемой точки.
Так как ширина выделенной полочки мала, гидростатическое давление и во всех точках её можно считать одинаковым и равным давлению в точках на оси полоски. Поэтому давление dR на всю полоску получим умножением значения указанного гидростатического давления на величину dF 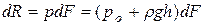 . Оно будет направлено нормально к стенке. Но, поскольку стенка состоит из ряда таких элементарных полосок, сила давления на всю стенку определяется суммированием сил давления на отдельные полоски
. Оно будет направлено нормально к стенке. Но, поскольку стенка состоит из ряда таких элементарных полосок, сила давления на всю стенку определяется суммированием сил давления на отдельные полоски 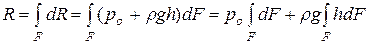
Интеграл 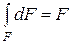 , а величина
, а величина 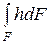 может быть представлена в виде
может быть представлена в виде 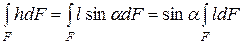 , где l – расстояние до любой полоски от поверхности жидкости, отсчитываемое в плоскости стенки.
, где l – расстояние до любой полоски от поверхности жидкости, отсчитываемое в плоскости стенки.
Величина 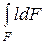 - статический момент площади F относительно линии пересечения поверхности жидкости с плоскостью стенки, она равняется F lс, где lс - расстояние от плоскости стенки до центра тяжести С этой площади. Следовательно,
- статический момент площади F относительно линии пересечения поверхности жидкости с плоскостью стенки, она равняется F lс, где lс - расстояние от плоскости стенки до центра тяжести С этой площади. Следовательно, 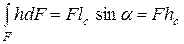 . Здесь hс = lс sin α - глубина погружения центра тяжести стенки. Тогда
. Здесь hс = lс sin α - глубина погружения центра тяжести стенки. Тогда 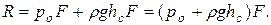
Замечая, что величина, стоящая в скобках, представляет собой гидростатическое давления в центре тяжести стенки, получаем окончательно:  , т.е. давление жидкости на плоскую, равно произведению величины смоченной площади стенки на гидростатическое давление в её центре тяжести.
, т.е. давление жидкости на плоскую, равно произведению величины смоченной площади стенки на гидростатическое давление в её центре тяжести.
Если давление на свободную поверхность жидкости в сосуде и на внешнюю поверхность стенки равно атмосферному, полное избыточное давление на стенку 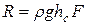 .
.
В случае, когда стенка расположена горизонтально (угол α = 0), т.е. представляет собой не боковую стенку, а горизонтальное дно сосуда, суммарное давление определяется по тем же формулам и составляет 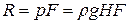 , где Н – высота столба жидкости в сосуде.
, где Н – высота столба жидкости в сосуде.
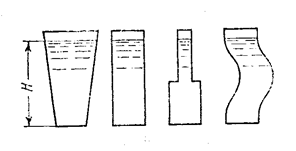
Рис.2.7
Следовательно, давление на дно зависит не от формы и объёма сосуда, а только от площади дна и высоты столба жидкости в сосуде. Поэтому для сосудов разной формы (рис. 2.7), заполненных одной и той же жидкостью до одного и того же уровня Н и имеющих одинаковую площадь дна, сила полного давления на дно будет одинакова.
Это свойство жидкости, на первый взгляд противоречащее обычным представлениям, известно под названием гидростатического парадокса.
Центр давления. Сила давления жидкости на стенку кроме значения и направления характеризуется также точкой её приложения. Эта точка называется центром давления.
Рассмотрим весьма часто встречающийся на практике случай, когда стенка имеет ось симметрии, лежащую в вертикальной плоскости. Центр давления в этом случае лежит на оси симметрии и для его определения остаётся найти только одну вертикальную координату. Для этого рассмотрим плоскую стенку (рис.2.9), аналогичную изображённую на рис.2.6, сохранив прежние обозначения.
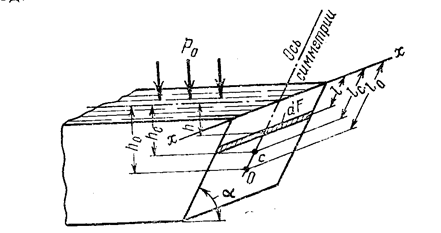
Рис.2.8
Используя теорему теоретической механики, о моменте равнодействующей (момент равнодействующей силы относительно некоторой оси равняется сумме моментов составляющих сил относительно той же оси), приравниваем сумму моментов сил давления, на элементарные площадки dF относительно оси х, совпадающей с линией пересечения поверхности жидкости с плоскостью стенки, к моменту равнодействующей силы давления на всю стенку F относительно той же оси: 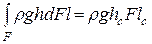
Здесь l – расстояние в плоскости стенки от оси до центра тяжести элементарной площадки (в пределе (при стремлении ширины элементарной полоски к нулю) это расстояние практически совпадает с расстоянием до центра давления элементарной полоски, а lо – расстояние от оси до центра давления 0 всей площади F.
Далее имея в виду, что 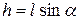 и
и 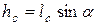 , где lс – расстояние в плоскости стенки от оси до центра тяжести с площади F, получаем:
, где lс – расстояние в плоскости стенки от оси до центра тяжести с площади F, получаем:
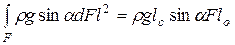 или
или 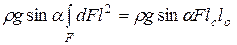 и
и 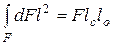
Как известно, выражение 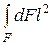 представляет собой момент инерции 1 площади стенки F относительно оси х. Следовательно,
представляет собой момент инерции 1 площади стенки F относительно оси х. Следовательно, 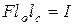 , откуда
, откуда 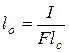 .
.
Полученное выражение часто оказывается более удобным представлять в другом виде, заменяя момент инерции площади относительно оси, совпадающей с урезом жидкости, моментом инерции Iс относительно оси, проходящей через центр тяжести. В теоретической механике между этими величинами устанавливается следующая зависимость: 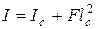 . (*)
. (*)
Подставив приведённое значение в выражение (*), получим окончательно: 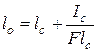 .
.
Из последнего выражения видно, что центр давления находится всегда ниже центра тяжести стенки (например, в случае прямоугольной стенки, одна из сторон которой совпадает с поверхностью жидкости, центр давления находится на 1/3, а центр тяжести на ½ её высоты от основания, т.е. от низа стенки).
Давление, действующее на криволинейную стенку. Чтобы получить общее решение, возьмём сосуд произвольной формы и выделим на его стенке какую-либо криволинейную поверхность S, ограниченную контуром AMBN (рис.2.9).
Будем искать составляющие полного давления на эту поверхность по координатным осям, выбрав, например, начало координат на свободной поверхности жидкости и расположив оси так, как это показано на чертеже. При этом ограничимся определением лишь одной составляющей Rx, параллельной оси х, поскольку остальные составляющие можно найти аналогичным образом.
Найдём проекцию поверхности S на некоторую плоскость NN, нормальную к оси х и расположенную между этой поверхностью и координатной плоскостью zOy. Отметим, что указанную плоскость проекций NN, как и направление самой оси х, можно выбрать по-разному.
На жидкость, заключённую в объёме между поверхностью S, плоскостью NN и поверхностью проектирующего цилиндра, образующие которого параллельны оси х, действуют следующие силы: тяжести (вес) Gx выделённого объёма жидкости; давления жидкости RFx на проекцию поверхности S на плоскость NN; давления на боковую поверхность указанного объёма (их проекция на ось х равна нулю); реакции R со стороны поверхности S, равная по значению, но обратная по направлению искомой силе давления жидкости.
Проектируя эти силы на ось х, имеем:
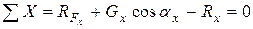 ,
,
откуда для проекции силы реакции получаем
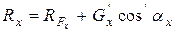 .
.
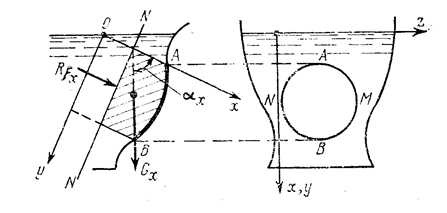
Рис.2. 9
Аналогично находят выражения для проекции силы реакции и на другие координатные оси: 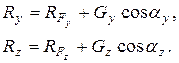
где αx, αy, αz - углы между направлением линии действия силы тяжести и осями координат x, y, z.
Таким образом, получаем следующую общую теорему о давлении на криволинейную поверхность: проекция силы давления на криволинейную поверхность S и на заданную ось х равна сумме проекций на эту ось веса жидкости, находящейся между поверхностью S, поверхностью проектирующего цилиндра и плоскостью проекций, нормальной к оси х, и силы давления жидкости на проекцию поверхности S на ту же плоскость проекции.
Относительное равновесие жидкостей. Определим силу полного давления со стороны жидкости на погружённое в неё дело.
Для этого рассмотрим некоторое тело произвольной формы объёмом V и плотностью ρ1, погружённое в жидкость плотностью ρ (рис.2.10), и найдём составляющие силы давления по координатным осям (оси x и y расположим в горизонтальной плоскости, ось z направим по вертикали).
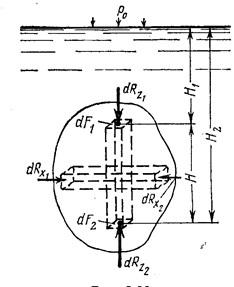
Рис.2.10
Найдём сначала составляющую давления по оси x, для чего разобьём тело на ряд весьма тонких горизонтальных призм с осями, параллельными этой оси. Так как, глубины погружений обоих оснований подобных элементарных призм под свободной поверхностью жидкости одинаковы и проекции площадей этих оснований равны и проекции давлений dR1 и dR2 на ось х, а поскольку при этом проекции давления на концевые площадки каждой призмы противоположны по направлению, то их сумма будет равна нулю. Это относится и к горизонтальной составляющей давления по оси y.
Для определения вертикальной составляющей разобьём тел на ряд элементарных вертикальных призм. Гидростатической давление в центрах тяжести торцевых площадок таких призм обозначим р1 и р2, а давление на свободной поверхности жидкости - ро.
Заменив эти давления их значениями в зависимости от глубины погружения площадок 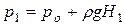 ;
; 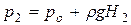 и обозначив нормальные к оси сечения призмы dF1 и dF2 (dF1 = dF2 = dF) для вертикальных составляющих давления на указанные площадки, получим:
и обозначив нормальные к оси сечения призмы dF1 и dF2 (dF1 = dF2 = dF) для вертикальных составляющих давления на указанные площадки, получим:
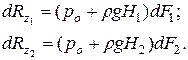
Эти две  силы различны по значению и противоположны по направлению. Первая направлена по вертикали вниз, вторая – вверх. Их равнодействующая будет
силы различны по значению и противоположны по направлению. Первая направлена по вертикали вниз, вторая – вверх. Их равнодействующая будет
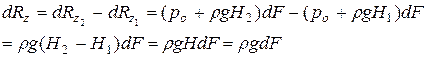
где Н – высота рассматриваемой элементарной призмы;
dV = НdF – объём этой призмы.
Сложив давления на все элементарные призмы, на которое разбито тело, получим:
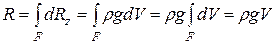
Таким образом, вертикальная составляющая давления со стороны жидкости на погруженное в неё тело направлена вверх и равна силе тяжести (весу) жидкости в объёме тела (закон Архимеда). Силу давления R при этом часто называют архимедовой подъёмной силой.
Из закона Архимеда следует, что на тело, погруженное в жидкость, в конечном счёте, действуют две силы: силы тяжести (вес тела) G и архимедова подъёмная сила R (рис.2.10).
При этом могут иметь место следующие основные случаи.
1. Плотность тела и жидкость одинакова (ρ1 = ρ).
Тогда 
Равнодействующая этих сил G – R = 0. Следовательно, тело будет находиться в состоянии безразличного равновесия, т.е. помещённое на любую глубину, оно не будет ни всплывать, ни тонуть.
2. Плотность тела больше плотности жидкости (ρ1> ρ). Следовательно, вес тела больше подъёмной силы (G > R) и их равнодействующая направлена вниз. Тело будет тонуть.
3. Плотность тела меньше плотности жидкости (ρ1< ρ). Значит, вес тела меньше подъёмной силы (G < R) и их равнодействующая направлена вверх. Погруженное в жидкость тело будет всплывать до тех пор, пока вследствие выхода части его над поверхностью жидкости подъёмная сила не уменьшится настолько, что станет равной весу тела. Подъёмная сила в этом случае называется поддерживающей.
Приборы - измеряющие давление. Приборы для измерения гидростатического давления можно подразделить на две основные группы: жидкостные и механические.
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр (рис.2.11) представляет собой стеклянную трубку небольшого диаметра обычно не менее 5 мм, открытую с одного конца. Второй конец трубки присоединён к сосуду, в котором измеряют давление.
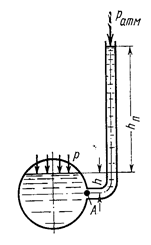
Рис.2.11
Пусть давление р на поверхности жидкости в сосуде будет выше атмосферного. Тогда жидкость в трубке пьезометра поднимается выше уровня жидкости в сосуде на некоторую высоту hп. Гидростатическое давление жидкости в точке А, взятой у основания пьезометрической трубки на глубине h от свободной поверхности жидкости в сосуде, определяется по основному уравнению гидростатики:
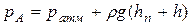
следовательно,
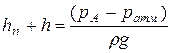
Кроме того, имеем 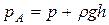 . Находим
. Находим 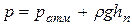
Давление, равное 1Па, соответствует ртутному столбу высотой 0,0075мм или водяному столбу высотой 0,102мм. Физическая атмосфера (1,033кгс/см2) определяется ртутным столбом высотой 760мм. Для нефтей и нефтепродуктов, имеющих меньшую плотность, высота столба жидкости в пьезометре, естественно, будет больше.
Пьезометр – очень чувствительный и точный прибор, однако он удобен только при измерении небольших давлений. Для значительных давлений трубка пьезометра должна быть чрезмерно длинной, что осложняет его применение. В этом случае используют так называемые жидкостные манометры, в которых давление уравновешивается не жидкостью, находящейся в сосуде, а жидкостью большей плотности. Обычно такой жидкостью является ртуть. Так как плотность ртути больше плотности воды в 13,6 раза, то трубка ртутного манометра оказывается значительно короче пьезометрической и сам прибор компактнее.
Ртутный манометр (рис2.12) представляет собой U -образную стеклянную трубку, изогнутое колено которой заполняется ртутью. Под действием давления р в сосуде уровень ртути в левом колене манометра понижается, а в правом – повышается.
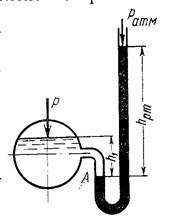
Рис.2.12
При этом гидростатическое давление в точке А, взятой на поверхности ртути в левом колене, определяется по:
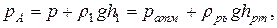
где ρ1, ρрт – плотность, соответственно, жидкости в сосуде и ртути. Отсюда
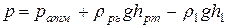 .
.
Для измерения высоких давлений применяют поршневой манометр, представляющий собой обращённый гидравлический пресс.
Поршневой манометр (рис.2.13) состоит из трубки А, через которую измеряемое давление р передаётся на поршень В, оканчивающийся широкой металлической пластинкой С.
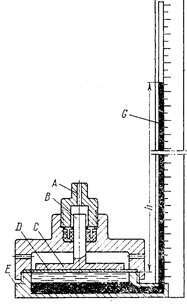
Рис.2.13
Под пластинкой находится резиновая диафрагма D, соприкасающаяся с водой, заполняющей короткое колено манометра Е. Нижнюю часть этого колена и открытую трубку G заполняют ртутью.
Если обозначить f – площадь поршня, F – площадь металлической пластинки, h – высоту ртути в манометрической трубке, то согласно уравнению равновесия
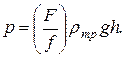
Из этого выражения видно, что поршневой манометр при сравнительно малой высоте ртутного столба позволяет измерять весьма высокие давления.
Дифференциальный манометр (рис.2.14) применяют в тех случаях, когда необходимо измерить не давление в сосуде, а разность давлений в двух сосудах (Аи В) или в двух точках жидкости в одном и том же сосуде.
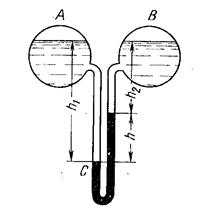
Рис.2.14
Здесь, как и раньше, для давления р на уровне поверхности ртути в левом колене (точке С) имеем
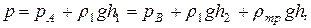
откуда
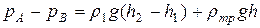
или поскольку 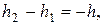
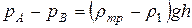
Таким образом, разность давлений определяется разностью уровней в двух коленах дифференциального манометра.
Для измерения давления ниже атмосферного (в сосуде имеется вакуум) служат приборы, называемые вакуумметрами.
Вакуумметры обычно измеряют не непосредственно давление, а вакуум, т.е. давление, не достающее до атмосферного. Они представляют собой заполненную ртутью изогнутую трубку, один конец которой А соединяется с сосудом В, где измеряется давление р, а другой С открыт.
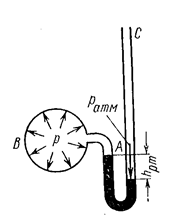
Рис.2.15
Применение приборов жидкостного типа, в том числе ртутных, ограничивается областью сравнительно невысоких давлений. Для измерений высоких давлений, применяют приборы второго типа - механические.
Пружинный манометр (рис.2.16) является наиболее распространенным из механических манометров.
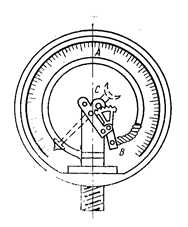
Рис.2.16
Он состоит из полой тонкостенной изогнутой латунной трубки (пружины А), один конец которой запаян и соединён посредством цепи В с зубчатым механизмом С. Второй, открытый конец трубки сообщается с сосудом, в котором замеряется давление. Через этот конец в трубку А поступает жидкость. Под действием давления пружина частично распрямляется и через зубчатый механизм приводит в движение стрелку, по отклонению которой определяют значение давления.
Кроме того, существуют так называемые мембранные манометры (рис.2.17), в которых жидкость воздействует на тонкую металлическую (или из прорезиненной материи) пластинку – мембрану.
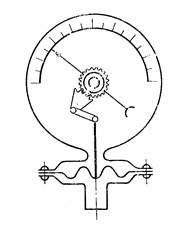
Рис.2.17
Деформация мембраны посредством системы рычагов передаётся стрелке, указывающей значение давления.