Тема 3. Методы изучения движения.
Модель гидравлического потока.
Типы потоков и гидравлические элементы. Скорость и расход.
Уравнение неразрывности. Формулы его выражения.
Физический смысл уравнения неразрывности.
Дифференциальное уравнение идеального движения жидкости.
Уравнение Бернулли для струйки и потока жидкости, его геометрический и физический смысл. Практическое применение уравнения Бернулли.
Методы изучения движения. Гидродинамикой называют раздел гидравлики, в котором изучаются законы движения жидкости. Если состояние жидкости в покое определяется лишь гидростатическим давлением, то её состояние в движении характеризуется ещё и скоростью движения её частиц. Из-за большого числа переменных величин, характеризующих движение жидкости, сложности наблюдаемых при этом явлений и трудности математического исследования действительное движение жидкости обычно заменяют некоторой условной, упрощённой схемой, рассматривающей поток жидкости, состоящий из отдельных элементарных струек. В гидравлике эту схему часто называют струйчатой моделью движения.
Для математического описания движения достаточно проследить за изменением скорости, давления и других величин в зависимости только от одной переменной – расстояния рассматриваемого поперечного сечения потока от некоторого начального его сечения. Подобное движение называют одномерным (или одноразмерным). Если полностью учитывают изменение скоростей, давлений по двум или трём координатным осям, движение соответственно называют двухмерным (двухразмерным) или плоским, трёхмерным (трёхразмерным) или пространственным. 2-х мерные и 3-х мерные движения рассматриваются в основном в теоретической гидродинамике. При этом движение жидкости представляется как непрерывная и последовательная деформация сплошной материальной среды. Его изучение имеет цель – выразить математически, в форме дифференциальных уравнений, основные кинематические и динамические характеристики как непрерывные функции координат и времени и может быть выполнено двумя методами: Лагранжа и Эйлер.
Метод Лагранжа заключается в наблюдении за движением одних и тех же, мысленно отмеченных, частиц жидкости, проходящих через различные точки пространства, и сводится к изучению траекторий этих частиц и прослеживанию во времени за изменением их кинематических характеристик.
По методу Эйлера объектом наблюдения являются кинематические характеристики различных частиц жидкости, непрерывно следующих одна за другой через определённые зафиксированные точки пространства. Метод Эйлера оказывается боле простым и удобным. Задавая внешние объёмные (массовые) силы проекциями их ускорений X, Y, Z, а скорости проекциями vx, vy, vz на координатные оси и присоединяя гидродинамическое давление р и плотность ρ, для каждой частицы такой идеальной однородной жидкости получаем 8 величин, определение зависимости которых от времени t и координат x, y, z и составляет содержание основных задач гидродинамики.
Для решения этих задач можно составить 5 уравнений, дающих зависимости между указанными 8-ю величинами, три из них при этом предполагаются заданными.
Модель гидравлического потока. Рассмотрим некоторую часть пространства заполненного движущейся жидкостью. В некоторой произвольной точке построим вектор скорости vb, изображающий (по значению и направлению) скорость частицы жидкости В, находящейся в данный момент времени в этой точке.
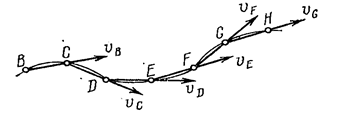
Рис.3.1
На этом векторе, на весьма малом расстоянии от точки В, возьмём точку С и построим вектор vс, соответствующий скорости частицы в этой точке в тот же момент времени и т.д. Получим ломаную линию BCDEFGH, стороны которой совпадают с направлениями векторов скоростей частиц жидкости B, C, D, E, F, G, H в данный момент времени.
Если безгранично уменьшать длину отрезков BC, CD, DE, EF, FG, GH, то в пределе ломаная линия превратиться в некоторую кривую, называемой линией тока – это кривая, проведённая через ряд точек в движущейся жидкости таким образом, чтобы векторы скоростей частиц жидкости, находящейся в данный момент в этих точках, являются к ней касательными.
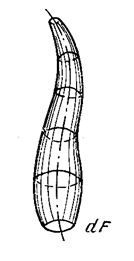
Рис.3.2
Выделим в жидкости элементарную площадку dF и через все её точки, находящиеся как внутри площадки, так и на контуре, проведём линией тока. Совокупность этих линий образует некоторый объёмный пучок, называемый элементарной струйкой жидкости.
Картина скоростей в каждый данный момент времени в пространстве, заполненном движущейся жидкостью, называется полем скоростей, а картина давлений - полем давлений.
Если скорость и давление в каждой данной точке пространства, заполненного движущейся жидкостью, остаются всё время постоянными (но могут меняться при переходе от одной точки пространства к другой), движение называют установившимся.
При установившемся движении элементарная струйка обладает следующими свойствами:
1) поскольку линии токов, из которых состоит струйка, с течением времени не меняют своей формы, то и форма всей струйки остаётся неизменной во времени;
2) ввиду того, что линии тока в данном случае являются и траекториями частиц жидкости, перетекание последней через боковую поверхность из одной струйки в другую невозможно; струйка как бы оказывается заключённой в жёсткие стенки, образующие некоторую трубчатую поверхность, называемую трубкой тока.
Типы потоков и гидравлические элементы. При изучении потоков жидкости вводят ряд понятий, характеризующих потоки с гидравлической и
геометрической точек зрения. Это: площадь живого сечения, периметр смачивания и гидравлический радиус.
Площадью живого сечения, или живым сечением потока, называют площадь сечения потока, проведённую нормально к направлению линией тока, т.е. нормально к направлению скоростей элементарных струек. Когда поток состоит из ряда расходящихся элементарных струек, живое сечение
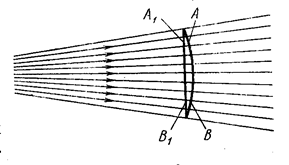
Рис.3.3
представляет собой криволинейную поверхность АВ. Но если расхождение струек невелико (движение называют в этом случае медленно изменяющимся), под живым сечением обычно понимают плоское сечение потока, нормальное к общему направлению движения жидкости.
Если стенки ограничивают поток полностью, движение жидкости называют – напорным; в случае частичного ограничения потока движение называют безнапорным. Напорные потоки, иногда называют - сплошь заполненными, а безнапорные – незаполненными.
Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного. Безнапорное же движение определяется постоянным давлением на свободную поверхность, обычно равным атмосферному.
Примером напорного движения может служить движение жидкости в трубопроводе при её перекачке насосами, истечение из резервуара или водонапорного бака, а примером безнапорного – движение жидкости в открытых каналах и реках.
Часть периметра живого сечения, по которому поток соприкасается с ограничивающими его стенками, называют периметром смачивания. При напорном – геометрический периметр и периметр смачивания совпадают по значению, а при безнапорном периметр смачивания будет отличен от геометрического, т.к. линия, по которой жидкость соприкасается с воздухом в длину периметра смачивания не входит.
Для канала периметр смачивания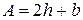 
, а геометрический равен 
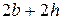. Отношение площади живого сечения к периметру смачивания 
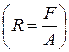, называют гидравлическим радиусом сечения.
При напорном движении в круглой трубе диаметром d геометрический радиус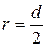 
, а гидравлический радиус 
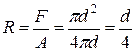. При движении
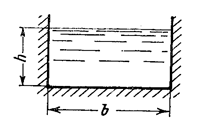
Рис.3.4
жидкости в открытом канале (рис.3.4)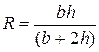 
, а понятие геометрического радиуса этому сечению вообще не присуще.
Скорость и расход. Расходом потока называют количество жидкости, протекающей через поперечное сечение потока в единицу времени. Количество протекающей жидкости, измеренное в объёмных единицах, носит название объёмного расхода и обозначается Q. Соответствующую объёмному расходу массу жидкости m называют массовымрасходом.
Между объёмным и массовым расходом существует следующая зависимость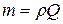 
. Единицы измерения объёмного расхода: [ м3/с; м3/час; л/с; л/мин ]. Единицы измерения массового расхода: [ кг/с; кг/час; кг/мин; т/с; т/час ]. Наряду с этим в гидравлике используют понятие весового расхода G и равнозначные ему понятия производительность, дебит, пропускная способность.
Расход элементарной струйки жидкости dQ может быть определён следующим образом. Обозначим dFa – площадь некоторого поперечного сечения струйки а-а (рис.3.5).
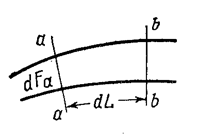
Рис.3.5
Тогда объём жидкости dQadt, прошедший через это сечение за весьма малое время dt, будет составлять dL.dFср, где dL – расстояние вдоль оси струйки, на которое перемещаются в течение указанного времени в сечении а-а; dFср – средняя на расстоянии dL площадь поперечного сечения струйки.
Отсюда имеет
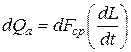
Здесь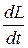 
– средняя на участке dL скорость течения жидкости, составляющей элементарную струйку.
Будем неограниченно уменьшать промежуток времени dt. Тогда в пределе, при dt →0, получим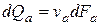 
.
Поскольку, сечение элементарной струйки было выбрано произвольно, то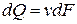 
,(**)
т.е. расход жидкости, проходящей через поперечное сечение элементарной струйки, равняется произведению площади поперечного сечения струйки на скорость в это сечении. Уравнение (**) называют уравнением расхода для элементарной струйки.
Если рассматривать поток жидкости как совокупность большого числа элементарных струек, то, общий расход жидкости Q для всего потока в целом можно определить как сумму элементарных расходов всех отдельных струек, из которых состоит поток.
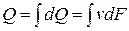
Предположим, что частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью, эту воображаемую фиктивную скорость называют средней скоростью потока (vср).
Таким образом, получаем уравнение расхода для потока в следующем виде: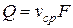 
. Из этого выражения находим 
.
Уравнение неразрывности. Формулы его выражения. Физический смысл уравнения неразрывности. Расход жидкости, подсчитанный по средней скорости, можно представить как объём цилиндра с площадью F и высотой vср (рис.3.6а).
Если расход определяется по действительным скоростям, закон распределения которых в поперечном сечении потока заде некоторой кривой, например параболой, значение его определяется объёмом соответствующего параболоида вращения с той же площадью основания F, как это и показано на (рис.3.6б).
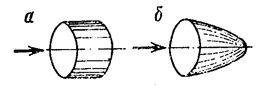
Рис.3.6
Если движение жидкости установившееся и при этом размеры и форма сечений вдоль потока не изменяются, следовательно, и средние скорости во всех поперечных сечениях потока одинаковы, движение называется равномерным.
Неравномерным называют такое установившиеся движение жидкости, при котором по длине потока изменяются его поперечное сечение и, следовательно, средняя скорость.
Равномерным, является движение жидкости в трубе постоянного диаметра с постоянным расходом жидкости, а неравномерным – движение жидкости в трубе переменного сечения.
Выделим сечениями а-а и b-b, отстоящими одно от другого на расстоянии dL, некоторый отсек той же элементарной струйки (рис.3.5). В этот отсек в единицу времени через сечение а-а втекает объём жидкости 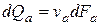, а через и b-b из него вытекает объём 
.
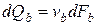Примем, что движение жидкости носит характер установившегося движения, жидкость несжимаема и в ней невозможно образование незаполненных пространств – пусто, т.е. соблюдается условие сплошности или неразрывности движения. Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку, как и отток из неё отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечения а-а и b-b, должны быть одинаковы.
Таким образом, 
, или 
.
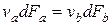Подобные соотношения можно составить для любых двух сечений струйки. Поэтому, в более общем виде получаем, что всюду вдоль струйки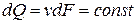 
.
Это уравнение представляет собой математическое выражение условия неразрывности. Оно называется уравнением постоянства расхода (уравнением неразрывности).
Перейдя к потоку в целом и используя понятие средней скорости, получим путём аналогичных рассуждений уравнение постоянства расхода для потока: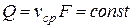 
Из этого уравнения следует 
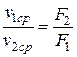, средние скорости поперечных сечениях потока при неразрывности движения обратно пропорциональны площадям этих сечений.
Дифференциальное уравнение идеального движения (уравнения Эйлера). Движение идеальной жидкости характеризуется отсутствием в ней сил внутреннего трения, вызывающих появление касательных напряжений. Поэтому силы давления в потоке подобной жидкости, как и в случае покоя, имеют только нормальную составляющую. Это позволяет при выводе дифференциальных уравнений движения воспользоваться полученными ранее дифференциаль-ными уравнениями гидростатики
, 
, 
(***)
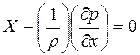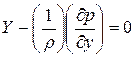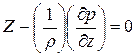Рассматриваемая жидкость несжимаема и однородна и в ней выделен некоторый элементарный объём в форме параллелепипеда со сторонами dx, dy¸dz, перемещающийся со скоростью v. Составляющие скорости по осям координат обозначим vx¸vy¸vz.
Уравнения равновесия для системы сил, действующих на этот находящийся в движении объём жидкости, могут быть получены, если на основании известного из теоретической механики принципа Даламбера к реально действующим, учитываемым уравнениям (***) силам (давления, объёмным и массовым) присоединить силу инерции.
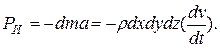
Знак минус указывает, что направление силы инерции противоположно направлению ускорения.
В (***) уравнениях все силы представлены в виде проекций на координатные оси и отнесены к единице массы рассматриваемого объёма жидкости.
Силы инерции, для составляющих этой силы по осям координат, отнесённым к единице массы:
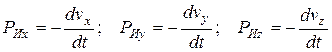
Следовательно,
, 
, 
(****)
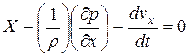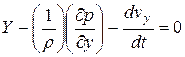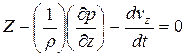В общем случае величины vx¸vy¸ и vz. являются функцией координат x, y¸z и времени t, поэтому их полный дифференциал, будет
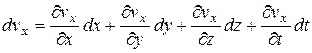
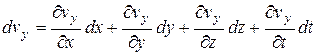
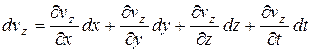
Эти выражения внесём в систему уравнений (****), имея в виду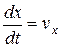 
; 
; 
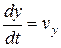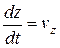, получим
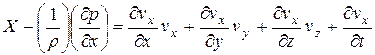
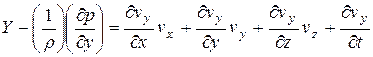
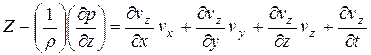
Эти уравнения – дифференциальные уравнения движения идеальной (невязкой) жидкости. Они устанавливают связь между проекциями объёмных, массовых сил и скоростей, давлением и плотностью жидкости и являются основой для изучения многих основных вопросов гидродинамики. Их называют уравнениями Эйлера.
Уравнение Бернулли для струйки жидкости. Уравнение Бернулли является основным в технической гидромеханике. Оно устанавливает зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки.
Выделим в пространственной элементарной струйке объём, ограниченный в некоторый момент времени t сечениями 1-1 и 2-2, нормальными к оси струйки О1О2 (рис.3.7).
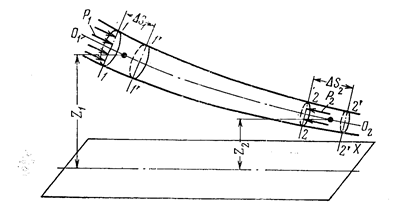
Рис.3.7
Первоначально жидкость будем считать идеальной, т.е. лишенной вязкости. Силы внутреннего трения в такой жидкости отсутствуют и к выделенному объёму струйки приложены только силы тяжести и силы гидродинамического давления. Пусть за некоторый малый промежуток времени dt указанный объём переместится в положение 1´- 1´ и 2´- 2´. Применим к его движению терему кинетической энергии, согласно которой приращение кинетической энергии движущейся системы материальных частиц равно сумме работ всех сил, действующих на систему. Эта теорема может быть выражена следующим простым уравнением:
(*)
где ∆W – приращение кинетической энергии; ΣΑ – сумма работ действующих сил.
Приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объёма V1´- 2´ и объёма V1 - 2. Замечая, что объём V1´- 2 входит как составная часть в выражения для объёмов V1- 2 и V1´- 2´:
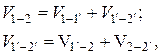
и имея в виду, что кинетическая энергия V1´- 2 пи установившемся движении жидкости одинакова как в момент времени t, так и в момент t + dt, приходим к выводу: искомое приращение кинетической энергии в конечном счёте определяется разностью кинетической энергии объёмов V2´- 2´ и V1 - 1´. Названные объёмы есть результат перемещения за время dt торцовых сечений выделенного участка элементарной струйки. Обозначив, v1 и v2 скорости в сечениях 1-1 и 2-2 найдём, что соответствующие перемещения будут равны v1dt и v2dt, а рассматриваемые объёмы:
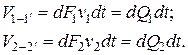
где dQ1 и dQ2 – значения расхода в сечениях 1-1 и 2-2.
Но по условию неразрывности расход во всех сечениях элементарной струйки одинаков (dQ1 = dQ2 = dQ) и, следовательно, V1 - 1´ = V2 - 2´ = dQdt. Масса же рассматриваемых объёмов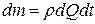 
.
Таким образом, выражение для приращения кинетической энергии можно записать в виде
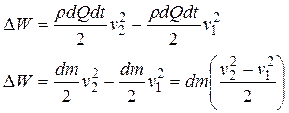
или
Определим работы сил, действующих на рассматриваемый объект жидкости. Работа силы тяжести равна произведению этой силы, на путь пройденный точкой её приложения, т.е. центром массы (тяжести) движущего объёма жидкости по вертикали. Рассматривая, как и ранее, выделенный объём струйки в двух его положениях состоящим из объёма V1´-2
и равных между собой объёмов V1 - 1´ и V2 - 2´, легко прийти к заключению, что работа АТ сил тяжести будет равна произведению силы тяжести объёма V1 - 1´ на расстояние по вертикали между центрами масс объёмов V1 - 1´ и V2 -2´ т.е.
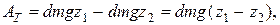
где z1 и z2 – расстояния по вертикали от произвольной горизонтальной
плоскости, называемой плоскостью сравнения, до центров масс
объёмов V1 - 1´ и V2 -2´, (т.е. вертикальные координаты центров
масс этих объёмов).
Силы давления, действующие на объём жидкости, складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работы сил давления на боковую поверхность равна нулю, так как эти силы во всё время движения нормальны к перемещению их точек приложения. Сумма работ сил давления ΣAД на торцевые сечения составляет
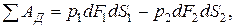
Где p1dF1¸ p2dF2 – силы давления на торцы 1-1 и 2-2; dS1, dS2 – элементарные перемещения точек приложения этих сил за время dt (работа сил давления на торец 2 отрицательна, так как направление силы p2dF2 противоположно перемещению dS2).
Но величины dF1dS1 и dF2dS2 есть равные между собой объёмы V1 - 1´ и V2 -2´ массы dm. Поэтому с учётом того, что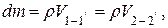 
выражение для суммы ΣAД можно представить в виде
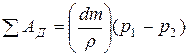
Подставив найденные выражения для работ сил и для приращения кинетической энергии в уравнение (*), получим
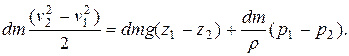
Разделим затем это уравнение на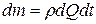 
, т.е. отнесём его к единице массы протекающей жидкости, и перегруппируем члены. Будем иметь
(**)
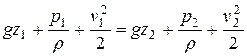Учитывая, что сечения 1-1 и 2-2 взяты произвольно, это уравнение можно распространить на всю струйку, применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:
(***)
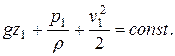Уравнения (**) и (***) представляют собой разную запись уравнения Бернулли для элементарной струйки идеальной жидкости. Сумму трёх слагаемых, входящих в уравнение (***), называют полной удельной энергией жидкости в данном сечении струйки и обозначают Э. Различают удельную энергию положения gz, удельную энергию давления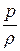 
и кинетическую удельную энергию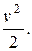 
В соответствии с этим уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии есть величина постоянная во всех сечениях струйки.
Физический и геометрический смысл уравнения Бернулли. Уравнение Бернулли для струйки идеальной жидкости по существу представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе его вывода значения работы сил, приложенных к выделенному объёму струйки, и значения кинетической энергии этого объёма были разделены на величину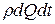 
.
Отсюда становится ясным, что поскольку член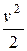 
есть мера кинетической энергии единицы массы движущейся жидкости, сумма членов 
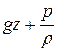будет мерилом её потенциальной энергии.
В отношении gz это очевидно. Действительно, если частица жидкости массы dm расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность её совершать работу, т.е. её потенциальная энергия относительно этой плоскости, равна dmgz. Будучи поделена на массу частиц dm, эта часть потенциальной энергии, называемая удельной потенциальной энергией положения, даст величину gz.
Для получения более ясного физического представления о том, что потенциальная энергия измеряется и величиной 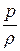, рассмотрим следующую схему. Пусть к трубе, заполненной жидкостью с избыточным давлением р, присоединён пьезометр, снабженный на входе краном. Кран сначала закрыт, т.е. пьезометр свободен от жидкости, и элементарный кольцевой объём жидкости dV массой ρdV перед краном находится под давлением р. Если затем открыть кран, жидкость в пьезометре поднимется на некоторую высоту 
.
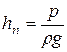Работа сил тяжести при этом перемещении объёма dV будет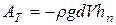 
.
Потенциальная же энергия единицы массы жидкости увеличится на величину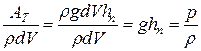 
Таким образом, единица массы, находящейся под давлением р, как бы несёт в себе ещё «заряд» потенциальной энергии, определяемый удельной энергией давления .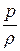
Под напором понимают энергию жидкости, отнесённую к единице силы тяжести, а не массы, как это было сделано ранее при выводе уравнения Бернулли.
В соответствии с этим получаем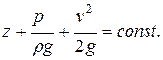 
- уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобной для гидравлических расчётов.
Аналогично будем различать напоры: полный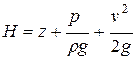 
, геометрический z, пьезометрический 
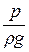и скоростной 
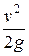. При этом, уравнение Бернулли можно сформулировать так: для элементарной струйки идеальной жидкости, полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров есть величина постоянная во всех её сечениях.
Между напором и удельной энергией существует простая зависимость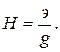 
Напор - измеряется единицами длины. Величиной z измеряется вертикальная координата центра тяжести сечения струйки. Единица измерения 
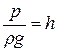и 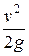- линейная (метр). Это даёт возможность строить графики уравнения Бернулли. По оси абсцисс откладывают расстояния по оси от некоторого сечения, принимаемые за начальные, а по оси ординат – значения составляющих напора для ряда сечений струйки.
Полный напор - обозначается буквой Н. В соответствии с уравнением 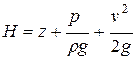, изменение полного напора вдоль струйки при движении идеальной жидкости изображают горизонтальной прямой 
.
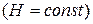Предположим, что элементарная струйка, произвольно расположенная в пространстве, несёт расход жидкости dQ. Тогда скоростной напор в любом сечении струйки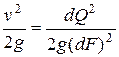 
, где dF – площадь сечения струйки.
Пусть напор относительно некоторой плоскости сравнения есть Н1 и ордината z оси струйки задана положением плоскости сравнения. Тогда можно вычислить значения пьезометрического напора в любом сечении струйки: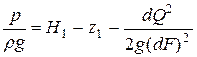 
.
Аналогично, если заданы положения плоскости сравнения, напор Н1 и значения пьезометрического напора для ряда сечений струйки, можно найти скоростной напор в этих сечениях: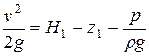 
и, следовательно, определить скорость v.
Плоскость сравнения назначается произвольно. Вычислив значения 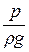и значения 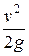, можно представить на одном графике изменения по длине струйки значений всех составляющих (z, 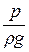, 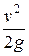) полного напора Н. Такой график (рис.3.8) будет называться графиком уравнения Бернулли. Кривая аа на этом графике называется пьезометрической линией. Она изображает изменение суммы геометрического и пьезометрического напоров
(z + 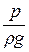) по длине струйки и является, характеристикой изменения, её удельной потенциальной энергии.
Изменение этой энергии, отнесённое к единице длины, носит название пьезометрической уклона и обозначается iп. Значение пьезометрического уклона для некоторого сечения струйки определяется выражением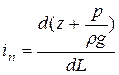 
при dL → 0, где dL – длина элементарного участка струйки, включающего рассматриваемое сечение.
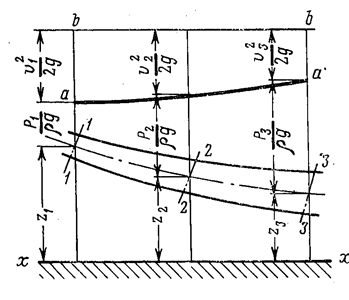
Рис.3.8
Выражение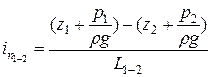 
определяет значение пьезометрического уклона на участке между сечениями 1-1 и 2-2 длиною L1-2,
а выражение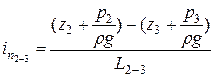 
– среднее значение пьезометрического уклона на участке между сечениями 2-2 и 3-3 длиной L2-3.
Уравнение Бернулли для элементарной струйки реальной жидкости. При движении идеальной жидкости её полная удельная энергия или напор Н сохраняет постоянное значение по длине струйки, то при движении реальной жидкости эта энергия будет убывать по направлению движения. Причина этому – неизбежные затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.Значит для струйки реальной жидкости полная удельная энергия в сечении 1-1
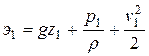
будет всегда больше, чем полная удельная энергия в следующем за ним некотором расстоянии сечении 2-2
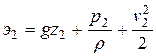
на величину указанных потерь энергии, и уравнение Бернулли вследствие этого принимает вид
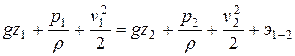
Подобно тому, как три члена левой части этого уравнения и три первых члена правой его части представляют собой полную удельную энергию жидкости соответственно в сечениях 1-1 и 2-2, так и величина э1-2 является мерой энергии, потерянной единицей массы жидкости на преодоление сопротивлений при её движении между указанными сечениями.
Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h1-2.
Следовательно, уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде
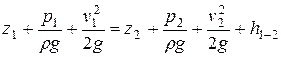
В соответствии с этим график уравнения Бернулли для струйки реальной жидкости (рис. 3.9) будет отличаться от аналогичного графика для идеальной жидкости (рис.3.8).
Поскольку в случае реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению движения, изменения его значений по длине струйки изображают некоторой кривой bb (в частном случае, когда струйка имеет постоянное сечение, потеря напора по её длине будет пропорциональна расстоянию от начального сечения и изменение полного напора изобразится как наклонная прямая).
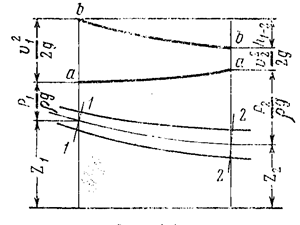
Рис.3.9
Уравнение Бернулли для целого потока реальной жидкости идентична записи для элементарной струйки
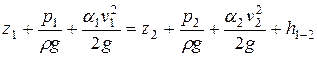
α1, α2 – коэффициент Кориолиса. Этот коэффициент представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при том же расходе, если бы все частицы жидкости обладали бы одинаковыми скоростями, равными средней скорости. Обычно коэффициент Кориолиса определяется опытным путём на основании измерений скорости в различных точках исследуемого потока. Он зависит от степени неравномерности распределения скоростей в его поперечном сечении и всегда больше единицы, Для так называемого ламинарного режима в цилиндрической трубе α =2, а для турбулентного α = = 1,045÷1,10. При практических расчётах часто принимают α =1, тем самым пренебрегая неравномерностью распределения скоростей о полагая, что все струйки как бы движутся с одной и той же средней скоростью.
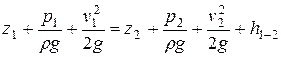
Практическое применение уравнения Бернулли. При помощи уравнения Бернулли выводятся формулы для определения расхода воды, проходящей через отверстия и водосливы, производится гидравлический расчёт трубопроводов многих водомерных устройств, выводится основное уравнение неравномерного движения жидкости и т.д. В гидравлике почти нет разделов, где уравнение Бернулли не использовалось бы в той или иной степени. Ограничимся теми задачами, где потерей напора при движении можно пренебречь.
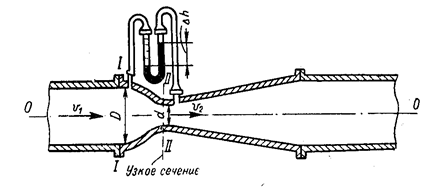
Рис.3.10
Водомер Вентури, представляет собой устройство, при помощи которого можно производить измерение расхода жидкости в трубах рис.3.10. Водомер Вентури состоит из конусообразной сходящейся трубы со вставкой меньшего диаметра, чем диаметр цилиндрической трубы, к которой присоединяется водомер. За вставкой следует конус водомера, расширяющийся в направлении течения. По оси прибора устанавливаются два пьезометра: один перед началом конусообразного сужения, а другой посредине суженной вставки. Введём следующие обозначения:
D – диаметр трубы, в которой производится измерение расхода
жидкости;
d – диаметр суженой вставки;
v1 – средняя скорость в трубе диаметром D;
v2 – средняя скорость, в области суженной вставки.
Применим уравнение Бернулли к потоку жидкости, движущейся через водомер Вентури. Для этого проведём плоскость сравнения по оси прибора и рассмотрим два сечения: первое I-I в начале сужения, где установлен первый пьезометр, и второе I I-I I – в суженной вставке, где установлен второй пьезометр.
Вследствие незначительной длины прибора между указанными сечениями (обычно 3-5 диаметров трубы) и плавного конусообразного подхода к суженной вставке потерями напора можно пренебречь, поэтому мы можем записать уравнение Бернулли применительно к рассматриваемому случаю следующим образом:
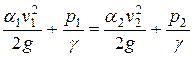
Геометрические высоты z1 и z2 равны нулю вследствие того, что плос