Основные законы алгебры логики

В законах описаны правила равенства (равносильности) функций. Функции считаются равными, если для любых комбинаций значений переменных их зна­че­ния совпадают.

1) переместительный закон (закон коммутативности):

(От перестановки слагаемых сумма не меняется и от перестановки сом­но­жи­телей произведение не меняется)

2) Сочетательный закон (закон ассоциативности)

(этот закон говорит о том, что операции одного приоритета можно вычис­лять как слева направо, так и справа налево)

 

3) Распределительный закон (закон дистрибутивности)

(Эти законы говорят о том, как раскрывать скобки. Первая форма этого за­ко­на аналогична закону обычной алгебры: , а вот вторая форма это­го закона аналога в обычной алгебре не имеет, но эту форму можно получить из первой, заменив все сложения на умножения, а умножения на сложения.)

 

4) Законы двойственности, или инверсии (законы де Моргана)

(Эти законы говорят о том, что операцию логического сложения можно заме­нить на логическое умножение и наоборот).

Законы де Моргана справедливы для любого количества переменных.

 

Законы алгебры логики доказывают с помощью таблиц истинности.

 

Докажем один из законов:

 

	A	B	C	A&B

 

Поскольку значения функций, стоящих слева и справа от знака равенства совпадают, следовательно функции равны.

Тождества

Правила поглощения и склеивания

Эти правила используют для упрощения логических функций. Доказываются эти правила с помощью законов и тождеств алгебры логики.

 

1)

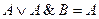
Доказательство:

 

2)

Доказательство:

 

3) 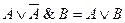(отрицание и следующая за ним операция поглощаются)

Доказательство:

 

4) (отрицание и следующая за ним операция поглощаются)

Доказательство:

Задачи

1) Проверить, будет ли верным условие, записанное на С/C++:

F = (a>b) && (b>c) || (c<d) && (b<=c) при a = 5, b = 3, с = 3, d = 7.

Решение:

1) a > b à 1 2) b>c à 0 3) c < d à 1 4) b <= c à 1

5) F = 1 & 0 1&1 = 1

Ответ: для данных значений переменных условие верно.

 

2) При каких значениях переменной x условие, записанное на С/C++, будет верно: F =!(x > 8 || x < -3).

Решение:

Обозначим (x > 8) как A, а (x < -3) как B, тогда

= (x <=8) && (x>=-3)

Ответ: -3 <= x <= 8

 

3) Упростить условие: F = (x > y) && (x <= y || у > z)

Решение:

Обозначим (x > y) как A, тогда (x <= y) соответствует .

(y > z) обозначим как B.

Тогда: (использовали 4 правило поглощения)

Ответ: F = (x > y) && (y>z)

 

4) Решить уравнение относительно X:

Для решения уравнения необходимо выразить X через другие переменные, для этого нужно упростить выражение, содержащее X.

Когда стоит отрицание над выражением, обычно убирают отрицание, ис­поль­зуя законы де Моргана:

Вынесем X за скобки, используя закон дистрибутивности: à

Ответ: (к сожалению не всегда ответ можно полу­чить так просто, в более сложных случаях для решения уравнения анализируют таблицы истинности).

 

5) Упростить функцию:

Решение:

(использовали закон де Моргана)

(использовали правило , где вмес­то A используется , а вместо B - )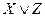

Ответ:

 

6) Упростить функцию:

Решение:

В первой скобке 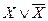дают 1, а если в выражение входит хотя бы одна еди­ни­ца, то все это выражение равно единице.

Ответ: (знаки умножения можно опустить, что мы и будем делать дальше, чтобы сократить запись выражений)

 

7) Упростить функцию:

Решение:

 

=

(подчеркнутые выражения сокращаются, поскольку A&A = A)

(использовали правила: и )

Ответ: F = XY.

 

8) Упростить функцию: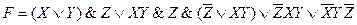

Решение:

(подчеркнутые части выражения сокращаются на основе правила )

(в подчеркнутой части выражения выносим за скобки)

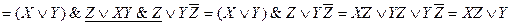
Ответ:

 

9) Упростить функцию:

Решение:

Когда над выражением стоит отрицание, можно сначала попробовать упрос­тить выражение под отрицанием, а потом убирать отрицание:

, поэтому

аналогично

Ответ:

Переход от табличной формы функции
алгебры логики к аналитической