Алгебра логики
Математическая логика – современный вид формальной логики, т.е. науки, изучающей умозаключения с точки зрения их формального значения.
До работ Дж.Буля сущность логических умозаключений сводилась к формальной схеме: «Все М суть Р; S есть М. Следовательно, S есть Р».
Содержание терминов S, Р и М для справедливости этих умозаключений безразлично. Умозаключения, составленные по этой схеме, ученые-схоласты назвали силлогизмами первой фигуры по модусу Barbara. До начала XIX века логика не выходила за рамки такого ряда силлогических умозаключений.
Однако, начиная с работ Дж. Буля, можно говорить о превращении её в математическую логику. Особенностью математической логики заключается в её аппарате, в преимущественном внимании к умозаключениям, применяемым в самой математике.
Математическая логика – это обширная наука, которая кроме традиционной проблематики занимается вопросами оснований математики и теории алгоритмов и имеет целый ряд приложений.
Так, Дж. Буль в своих работах сделал попытку свести логику (вернее логику высказываний) к алгебраическим формам, установив систему аксиом символической логики высказываний, которая определила, тем самым методы исследования и решения «логических уравнений». Создание алгебры логики явилось попыткой разрешить традиционные задачи логики чисто алгебраическими методами. Логическое исчисление Дж. Буля стали называть «булевой алгеброй».
Следует заметить, что логика Буля основывается на отношении эквивалентности, при котором левая часть равенства всегда содержит ровно столько же истины, сколько и правая. Следовательно, такая логика не привносит нисколько нового знания. Логика высказываний и логика предикатов (две другие части математической логики) построены на отношении порядка, при котором правая часть логического выражения (заключение) содержит уже больше истины, чем левая (посылка).
В дальнейшем идеи Дж. Буля были развиты, было также показано, что алгебра Буля является частным случаем более общих алгебраических структур, но одновременно «булева алгебра» нашла свое широкое применение в моделировании технических систем, в управлении и стала основой в разработке компьютерных дискретных систем.
Третий раздел пособия посвящен именно булевой алгебре, булевым функциям и их применениям, а уже в четвертом разделе будут рассмотрены вопросы логики высказываний.
Логические функции
Рассмотрим множество В={0,1}. Такой выбор множества можно интерпретировать как переменную, принимающую два различных значения: “ложь” или “истина” в высказывании, “отсутствие” или “наличие” признака и т. п. В ЭВМ вся информация представляется в двоичных кодах, как и во всех цифровых системах. Моделирование таких систем основано на использовании двузначной логики, в которой переменная принимает значение из В.
В общем случае логические переменные могут принимать одно из k значений (k-значная логика). Перечень всех k символов В`={a1, a2,..., aк} составляют алфавит, а сами символы ai буквы алфавита.
Алгебра, образованная множеством В вместе со всеми операциями на нём, называется алгеброй логики.
Логической функцией f от n переменных называется n-арная операция на В, которая может быть также представлена как отображение f: В x В x... x В ® В. Очевидно, что f(x1,x2,...,xn) Î В и хi Î В, i= 
Всякую логическую функцию от n переменных можно задать таблицей из 2n строк. Например, для n=3 таблицу аргументов заполним, начиная с (0, 0, 0) и прибавляя 1 (двоичное сложение) каждый раз справа. Получим таблицу 3.1.
В таблице приведена одна из возможных булевых функций трех переменных. Набор аргументов, при которых f=1 называют единичными наборами, а при которых f=0 - нулевыми наборами. Очевидно, что существует всего  различных функций n переменных. В качестве примера рассмотрим функцию одной переменной и составим таблицу 3.2., из которой можно заметить, что f0=0 и f3=1 являются константами, не зависящими от значения аргумента, который становится несущественным.
различных функций n переменных. В качестве примера рассмотрим функцию одной переменной и составим таблицу 3.2., из которой можно заметить, что f0=0 и f3=1 являются константами, не зависящими от значения аргумента, который становится несущественным.
Таблица 3.1.
| x1 | x2 | x3 | f(x1 ,x2,x3) |
Таблица 3.2.
| x | f0 | f1 | f2 | f3 |
В общем случае переменная хi (функции n переменных) называется несущественной (фиктивной) в функции f(x1,..., x i,...,xn), если f(x1,..., 0,...,xn) = f(x1,..., 1,...,xn) при любых наборах остальных аргументов. Очевидно, что в этом случае мы получим функцию n -1 переменных. Так, например, f(x1, x2, x3)=g (x1, x2), если х3 – фиктивный аргумент, а для f0 и f3 из таблицы 3.2 фиктивной переменной является единственная переменная х. Для функций f1 и f2 из таблицы 3.2 можем записать f2=x и f1= «не х» = «отрицание х».
Большое значение отводится в прикладных вопросах функциям двух переменных. Рассмотрим таблицу истинности этих функций (таблица 3.3).
Таблица 3.3
| x1 | x2 | j0 | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 | j13 | j14 | j15 |
Для этих функций существует специальное обозначение и названия (таблица 3.4).
Таблица 3.4
| Функция | Обозначения | Название функции | Чтение | Булева формула | ||
| j0 | Константа 0 | любое 0 | ||||
| j1 | х1 & x2 х1·х2, х1 Ù х2 | Конъюнкция | х1 и х2 | 
| ||
| j2 | х1 х2 х1 Ü х2 х1 Ì х2 | Отрицание импликации | х1, но не х2 | 
| ||
| j3 | х1 | Повторение х1 | как х1 | 
| ||
| j4 | х2 х1 х2 Ü х1 х2 Ì х1 | Отрицание обратной импликации | х2, но не х1 | 
| ||
| j5 | x2 | Повторение x2 | как x2 | 
| ||
| j6 | x1 Å х2 х1 º х2 | Сумма по модулю 2; неравнозначность | или х1, или х2 | 

| ||
| j7 | х1 Ú х2 | Дизъюнкция | х1 или х2 | 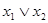
| ||
| j8 | х1 ¯ х2, x1 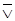 x2 x2
| Стрелка Пирса, функция Вебба | не х1 и не х2 | 
| ||
| j9 | х1 ~ х2 | Эквиваленция; Равнозначность |
| 

| ||
| j10 | 
| Отрицание х2 | не х2 | 
| ||
| j11 | х2®х1 х2 Þх1 х2Éх1 | Обратная Импликация | если х2, то х1; из х2 следует х1 | 
| ||
| j12 | 
| Отрицание х1 | не х1 | 
| ||
| j13 | х1 ® х2 х1 É х2 х1Þх2 | Импликация | если х1, то х2; из х1 следует х2 | 
| ||
| j14 | х1|х2, х1  х2 х2
| Штрих Шеффера | не х1 или не х2 | 
| ||
| j15 | Константа 1 | любое 1 |
Очевидно, что у функций j0 и j15 обе переменные - фиктивные, у функций j3 и j12 фиктивной переменной является х2, а у функций j5 и j10 - х1.
С ростом числа переменных (n®¥) число функций с фиктивными переменными уменьшается и стремится к 0. Ранее мы ввели понятие суперпозиции функции f и g как f  g, которую мы можем в общем случае распространить на m функций f1, f2,..., fm как f1
g, которую мы можем в общем случае распространить на m функций f1, f2,..., fm как f1  f2
f2  ...
...  fm. Результатом суперпозиции является некоторая функция f, полученная подстановкой этих функций одной в другую:
fm. Результатом суперпозиции является некоторая функция f, полученная подстановкой этих функций одной в другую:
f(·)=fm(fm-1(... (f1(·))...).
Формулой называется выражение, описывающее эту суперпозицию. Символы переменных х1, х2..... хn будем считать формулами глубины 0. Полагаем также, что задано (конечное или бесконечное) множество функций S ={f1, f2,..., fm,...}.
Формула F имеет глубину k+1, если F имеет вид fi(F1,..., Fni), где fi ÎS, ni - число аргументов функции fi, а F1,..., Fni - формулы, максимальная из глубин которых равна k. F1,..., Fni называются подформулами F; fi называется внешней или главной операцией формулы F.
Например, f2(x1, x2, x3) - это формула глубины 1, а f3(f1(x1,x2), f2 (x1, f3,(x1, x2))) - формула глубины 3, содержащая одну подформулу глубины 2 и одну - глубиной 1. Если использовать инфиксную запись функции (знаки функции стоят между аргументами) и если f1 - дизъюнкция, f2 - сложение по модулю 2, f3 - конъюнкция, то последняя формула имеет вид:
 . (3.1)
. (3.1)
Все формулы, построенные таким образом, то есть содержащие только символы переменных, скобки и знаки функций из множества S, называются формулами над S.
Вычисление формулы производится с вычисления подформул на оценке списка переменных (<x1, x2, x3> для случая (3.1)). Например, для <1, 0, 1> в формуле (3.1) получим
 .
.
Поскольку число функций любого конечного числа переменных ограничено (конечно), а разнообразие формул неограниченно, то любая из функций может быть представлена множеством формул. Таблицы истинности таких формул совпадают при любых значениях переменных. Эти формулы называются равносильными или эквивалентными. Например, по таблице истинности можно установить эквивалентность таких формул:
формулы

с таблицей истинности:

| 
| 
| 
| 
| 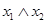
| F1 |
и формулы 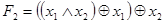 , которая имеет таблицу истинности:
, которая имеет таблицу истинности:

| 
| 
| 
| F2 |
Таким образом, формулы F1 и F2 ,имеющие одинаковые таблицы истинности, реализуют одну и ту же функцию – дизъюнкцию.
Другим способом установления равносильности формул могут быть эквивалентные преобразования.
Булева алгебра
Рассмотрим возможность представления логических функций в виде суперпозиций функций И, ИЛИ, НЕ (Ù, Ú,`).
Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма. Введём обозначение х0=`х, х1=х. Пусть a - параметр, равный 0 или 1. Тогда xa =1, если х= a, и хa=0, если х¹a.
Теорема 3.1. Всякая логическая функция  может быть представлена в следующем виде:
может быть представлена в следующем виде:

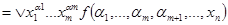 , (3.2)
, (3.2)
где m £ n, а дизъюнкция берется по всем  наборам значений переменных
наборам значений переменных  .
.
В формуле (3.2) и далее мы часто конъюнкцию  для сокращения записи и удобства будем изображать просто
для сокращения записи и удобства будем изображать просто  .Именно так необходимо понимать запись в формуле (3.2).
.Именно так необходимо понимать запись в формуле (3.2).
Равенство (3.2) называют разложением по переменным х1, х2,...,хm. Например для n=4, проведем разложение (3.2) по х1 и х2, то есть m=2:

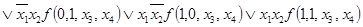 .
.
Теорема легко доказывается подстановкой произвольной оценки списка переменных <d1, d2,..., dm, dm+1,..., dn>. Так как  , если только
, если только  , то среди всех
, то среди всех  конъюнкций
конъюнкций  в правой части (3.2) в 1 обратится только одна - та, в которой a1=d1, a2=d2,..., am=dm. Все остальные конъюнкции равны 0. Таким образом, из (3.2) получаем
в правой части (3.2) в 1 обратится только одна - та, в которой a1=d1, a2=d2,..., am=dm. Все остальные конъюнкции равны 0. Таким образом, из (3.2) получаем

 ,
,
тождество, которое и доказывает справедливость теоремы.
Рассматривая предельные случаи, запишем для m=1:
 ,
,
что является разложением по х1, но аналогично можно записать для любой переменной хi. Другой предельный случай - разложение по всем n переменным:

 , (3.3.)
, (3.3.)
где дизъюнкция берется по всем оценкам списка переменных, соответствующих единичным наборам функции (по таблице истинности это строки, в которых f=1), т.к. нуль-наборы не вносят вклада в формулу. Разложение (3.3) называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f. Для каждой функции f её СДНФ содержит столько конъюнкций, сколько единичных наборов в таблице истинности для функции f.
Каждой оценке <d1, d2,..., dn> в формуле (3.3) соответствует конъюнкция, в которой  берется с отрицанием, если di=0 и без него, если di =1. Например, для эквиваленции (j9 в таблице 3.3.) СДНФ будет иметь вид
берется с отрицанием, если di=0 и без него, если di =1. Например, для эквиваленции (j9 в таблице 3.3.) СДНФ будет иметь вид
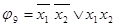 .
.
Очевидно, исходя из (3.3), можно утверждать, что для каждой функции f(х1, х2,..., хn) существует взаимно однозначное соответствие между f и её СДНФ и, следовательно, СДНФ для всякой логической функции единственна (с точностью до порядка букв и конъюнкций). Так, например, для функции, заданной в таблице 3.1 СДНФ имеет вид:
 .
.
Единственная функция, не имеющая СДНФ, - константа 0. Формулы, содержащие, кроме переменных и скобок, только знаки дизъюнкции, конъюнкции и отрицания  , называют булевыми формулами. Следствием формулы (3.3) является следующая теорема.
, называют булевыми формулами. Следствием формулы (3.3) является следующая теорема.
Теорема 3.2. Всякая логическая функция может быть представлена булевой формулой.
Действительно, для всякой функции (кроме константы 0) таким представлением может служить её СДНФ в соответствии с (3.3). Константу 0 можно представить булевой формулой  .
.
Введём теперь корректное понятие алгебры. Пусть функция  , и будем называть её n-арной операцией на множестве M, причём n называется арностью операции j. Множество M с заданной на нём совокупностью операций
, и будем называть её n-арной операцией на множестве M, причём n называется арностью операции j. Множество M с заданной на нём совокупностью операций  , то есть система
, то есть система  называется алгеброй; М - называется основным, или несущим, множеством (или просто носителем) алгебры А. Вектор арностей операций алгебры называется её типом, совокупность операций F - сигнатурой.
называется алгеброй; М - называется основным, или несущим, множеством (или просто носителем) алгебры А. Вектор арностей операций алгебры называется её типом, совокупность операций F - сигнатурой.
Например, алгебра (R; +, ·) называется полем действительных чисел. Обе операции - бинарные, поэтому тип этой алгебры (2,2).
Алгебра (Р2; Ú, Ù,`), основным множеством которой является всё множество логических функций, а операциями являются дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций. Операции булевой алгебры часто называют также булевыми операциями.
Очевидно, что дизъюнкция и конъюнкция являются бинарными операциями, а отрицание - унарной операцией. Тогда булева алгебра является алгеброй типа (2, 2, 1).
Фактически, как правило, мы имеем дело не с функциями, а с формулами, представляющими эти функции. Так как каждую функцию представляет неограниченное множество формул, то мы оперируем с алгеброй формул, а не функций. Чтобы алгебра формул соответствовала алгебре функций, среди всего множества формул выделяют классы эквивалентных формул. Это множество класса формул и является несущим или основным для алгебры формул. Результатом, например, дизъюнкции классов K1 и K2 считается класс всех формул, эквивалентных F1 Ú F2, где F1 Î K1, F2Î K2.
Такое определение алгебры классов формул называется алгеброй Линденбаума-Тарского. Она изоморфна булевой алгебре функций. Только всегда нужно учитывать, что логическая схема на выходе реализует функцию от входов; когда же речь ведётся об эквивалентных преобразованиях, упрощениях и т. д., то имеется в виду преобразования формул, реализующих одну и ту же функцию.
Для булевых функций имеют место следующие равносильности, которые называют также свойствами булевых функций.
1. Идемпотентность:
 . (3.4)
. (3.4)
2. Коммутативность:
 . (3.5)
. (3.5)
3. Ассоциативность:
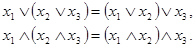 (3.6)
(3.6)
4.  Законы поглощения:
Законы поглощения:
 (3.7)
(3.7)
 5. Дистрибутивность:
5. Дистрибутивность:
 (3.8)
(3.8)
6. Свойства константы 1:
 . (3.9)
. (3.9)
7. Свойства константы 0:
 . (3.10)
. (3.10)
8. Двойное отрицание:
 . (3.11)
. (3.11)
9. Закон де Моргана:
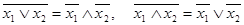 . (3.12)
. (3.12)
10. Правило исключения третьего и закон непротиворечия:
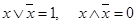 . (3.13)
. (3.13)
Справедливость соотношений (3.4)-(3.13) может быть проверена вычислением обеих частей равенств на всех наборах значений переменной. Они остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь сообщить правило подстановки формулы вместо переменной: при подстановке формулы F, вместо х все вхождения х в исходные выражения должны быть одновременно заменены формулой F. Правило подстановки позволяет получать новые эквивалентные соотношения из (3.4)-(3.13).
Во всякой алгебре равенство F1=F2 означает, что формулы F1 и F2 описывают один и тот же элемент алгебры, то есть в нашем случае одну и ту же логическую функцию f1. Следовательно, если формула F содержит F1 в качестве подформулы, то замена F1 на F2 не изменяет элемента булевой алгебры F над которым производятся операции в формуле F. Поэтому формула F`, полученная из F такой заменой, эквивалентна F. Это утверждение является правилом замены подформул, позволяющее, используя эквивалентные соотношения, получать эквивалентные формулы.
Например, для (3.12) подставим `х1х3 вместо х1:

и все формулы в этом ряду эквивалентны между собой.
Можно, используя эквивалентные соотношения и правила замены, получить совокупность основных эквивалентных преобразований. Эти преобразования являются мощным средством доказательства эквивалентности формул и, как правило, более мощным, чем их вычисления, на наборах значений переменных.
Законы упрощения формул
а) поглощение:
 . (3.14)
. (3.14)
 . (3.15)
. (3.15)
Доказательство: Из (3.10) и (3.11) следует, что 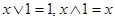 и, используя (3.7), получим:
и, используя (3.7), получим:
 .
.
Точно также из (3.6) и (3.14) получаем: 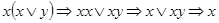 .
.
б) склеивание:  . (3.16)
. (3.16)
Доказательство: из (3.6) в обратном порядке и из (3.13) получим
 .
.
в) обобщенное склеивание:
 . (3.17)
. (3.17)
Доказательство проведем с помощью “расщепления”, то есть применим (3.16) в обратном порядке:
 ,
,
затем для 1-го и 3-го, а затем для 2-го и 4-го членов, попарно используя (3.14), получим:
 ,
,
 ,
,
откуда следует, что:  .
.
г)  . (3.18)
. (3.18)
Доказательство:  ,
,
или, используя (3.7), сразу же  .
.
д.) обобщением равенств (3.14) и (3.18) является равенство
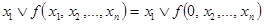 (3.19)
(3.19)
При доказательстве (3.19) можно использовать разложение по  , (3.14) и (3.18):
, (3.14) и (3.18):

 .
.
Приведение к дизъюнктивной нормальной форме (в том числе к СДНФ)
Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций. Из (3.17) следует, что ДНФ функции может быть не единственной.
Приведение к ДНФ осуществляется последовательным применением (3.8) и (3.12), с помощью которых все отрицания “опускаются” до переменных. Затем раскрываются скобки, а с помощью (3.1), (3.12),(3.13) и (3.10) удаляются лишние конъюнкции, повторения переменных в конъюнкциях и удаляются константы.
Например:
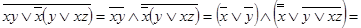
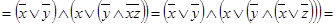


Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, например, для формулы с тремя переменными имеем:
 . (3.20)
. (3.20)
Если из формулы F1 с помощью некоторых эквивалентных соотношений можно получить формулу F2, то F1 можно получить из F2, используя те же соотношения в обратном порядке, то есть всякое эквивалентное преобразование обратимо.
Теорема 3.3. Для любых двух эквивалентных формул F1 и F2 существует эквивалентное преобразование F1 в F2 с помощью соотношений (3.4)-(3.13).
Доказательство. Действительно, преобразуем F1 и F2 в СДНФ. Поскольку F1 и F2 эквивалентны, то их СДНФ совпадают. Обратив второе преобразование, получим преобразование F1 Þ СДНФ Þ F2. Таким образом, соотношений (3.4) -(3.13) достаточно для любого эквивалентного преобразования в булевой алгебре.
Приведение к конъюнктивной нормальной форме
Аналогично ДНФ определяется конъюнктивная нормальная форма (КНФ) как конъюнкция элементарных дизъюнкций. От ДНФ к КНФ переход осуществим следующим образом. Пусть ДНФ имеет вид F= k1 Ú... Ú km, где ki- элементарные конъюнкции. Формулу k1Ú...Ú km преобразуем следующим образом:
 ,
,
где 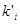 – элементарные конъюнкции, отличные от
– элементарные конъюнкции, отличные от  .
.
Тогда  . По правилу де Моргана отрицания элементарных конъюнкций преобразуем в элементарные дизъюнкции, что и дает КНФ.
. По правилу де Моргана отрицания элементарных конъюнкций преобразуем в элементарные дизъюнкции, что и дает КНФ.
Например, ДНФ из (3.20) преобразуем в КНФ:


 .
.
Аналогом СДНФ является СКНФ - совершенная конъюнктивная нормальная форма, каждая элементарная дизъюнкция которой должна содержать все переменные. Переход от КНФ к СКНФ можно всегда осуществить, используя (3.16) после преобразования:
 ,
,
или, заменяя  на
на  , получим
, получим
 . (3.21)
. (3.21)
Теперь для функции трёх переменных (x, y, z), у которой в КНФ одна из элементарных дизъюнкций имеет вид (x Ú`y), может быть на основании(3.21) представлена в виде:
 ,
,
то есть элементарные дизъюнкции будут содержать все переменные, что и требуется для СКНФ. Единственной функцией, не имеющей СКНФ, является константа 1.
Двойственность
Пусть заданы две функции n переменных: 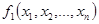 и
и  . Функция
. Функция 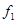 называется двойственной к
называется двойственной к  , если
, если
 . (3.22)
. (3.22)
Взяв отрицание от обеих частей в (3.22) и одновременно подставляя  вместо
вместо  , получим:
, получим:
 ,
,
откуда следует, что  двойственна
двойственна 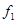 . Свойство двойственности между логическими функциями симметрично. Из определения двойственности следует, что для любой функции двойственная ей функция определяется однозначно. Некоторые функции являются двойственными самим себе. Такие функции называются самодвойственными.
. Свойство двойственности между логическими функциями симметрично. Из определения двойственности следует, что для любой функции двойственная ей функция определяется однозначно. Некоторые функции являются двойственными самим себе. Такие функции называются самодвойственными.
Рассмотрим некоторые примеры.
а) 
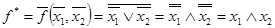 .
.
Таким образом, конъюнкция и дизъюнкция являются двойственными функциями.
б) константа 1 двойственна 0 и наоборот.
в) отрицание самодвойственно.
г) 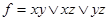 . Тогда:
. Тогда:




 .
.
Таким образом, используя эквивалентные преобразования и упрощения (3.4)-(3.15), мы получили, что функция f самодвойственна.
Утверждение. Если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную f.
Это утверждение, называемое принципом двойственности, нетрудно доказать, пользуясь определением двойственности и прямой выкладкой.
В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из приведенных выше примеров: если в формуле F, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F*, представляющую функцию f*, двойственную f.
Теорема 3.4. Если  , то
, то 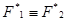 .
.
Доказательство. Действительно, пусть F1ºF2, <х1, х2,..., хn> - список переменных, от которого зависят F1, F2 (и, очевидно, F*1, F*2). Если <t1, t2,..., tn> - оценка этого списка, то F*1 принимает значение 1 на этой оценке только в том случае, если (F*1)* (т.е. F1) принимает значение 0 на оценке <s1, s2,..., sn>, двойственной оценке <t1, t2,..., tn>. Последнее, в силу равносильности F1 и F2, имеет место лишь тогда, когда F2 принимают значения 0 на оценке <s1, s2,..., sn>. С другой стороны, F*2 принимает значение 1 на <t1, t2,..., tn> только тогда, когда (F*2)*, (т.е. F2) принимает значение 0 на <s1, s2,..., sn>. Таким образом, истинность F*1 на <t1, t2,..., tn> равносильна истинности F*2 на <s1, s2,..., sn>. Так как оценка < t1, t2,..., tn > произвольна, то F*1ºF*2. Естественно, что утверждение теоремы справедливо и для функций, представляемых формулами: f1ºf2 и f*1ºf*2.
Принцип двойственности можно с успехом применять и для формулирования новых равносильностей, например, из соотношения  , заменив операции Ú на Ù и наоборот, получаем равносильность
, заменив операции Ú на Ù и наоборот, получаем равносильность 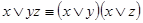 . Возможны и другие применения принципа двойственности. Например, вспомним, что всякая функция
. Возможны и другие применения принципа двойственности. Например, вспомним, что всякая функция  (исключая константу 0) может быть представлена своей СДНФ
(исключая константу 0) может быть представлена своей СДНФ
 , (3.22)
, (3.22)
где дизъюнкции берутся по всем оценкам <a1, a2,..., an>, которых  (а не только по
(а не только по  , как в (3.3)). Тогда для двойственной функции имеем
, как в (3.3)). Тогда для двойственной функции имеем
 ,
,
где конъюнкции берутся тоже по всем оценкам.
Учитывая, что  на этих оценках принимает значения 0 или 1 и свойства (3.10), получим
на этих оценках принимает значения 0 или 1 и свойства (3.10), получим
 , (3.23)
, (3.23)
на оценках 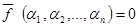 (или
(или  ), что является СКНФ.
), что является СКНФ.
Тогда, очевидно, справедливо утверждение, что каждой логической n-местной функции f(x1,x2,..., xn), где n³1 и f ¹1 соответствует такая формула F, зависящая от списка переменных <x1,x2..., xn> и находящаяся в СКНФ относительно этого списка, что F выражает собой f(x1,x2..., xn). Формула F определена однозначно с точностью до перестановки конъюнктивных членов.
Для доказательства положим, что изначально f выражена формулой F0. Тогда найдём двойственные им f* и F0*, представим f* в виде СДНФ по формуле (3.3). Получим формулу F1 и ещё раз найдём двойственную (f*)*ºf. СДНФ F1 будет представлена в этом случае в виде СКНФ F1* (3.23). Таким образом, каждой функции f соответствует своя СКНФ, и это соответствие взаимно однозначное, так как все преобразования, выполненные в процессе доказательства, однозначные или эквивалентные.
Легко показать, что, исходя из способа получения СКНФ, каждая логическая функция может быть представлена в виде разложения

 (3.24)
(3.24)
а учитывая свойства (3.10) можем записать:
Учитывая, что x v 1 = 1, то разложение в СКНФ имеет вид
 ,
,
или
 .
.
Тогда, например, для конъюнкции из таблицы истинности (табл. 3.3) можем сразу записать в форме СКНФ, взяв на нуль наборах сопряженные значения аргументов
 .
.
Функционально полные системы логических функций
Система логических функций  называется функционально полной системой, если любая логическая функция может быть выражена через функции
называется функционально полной системой, если любая логическая функция может быть выражена через функции  с помощью их суперпозиции (быть выражена формулой над
с помощью их суперпозиции (быть выражена формулой над  ).
).
Из (3.3) следует, что система  является функционально полной. Очевидно, что любая система
является функционально полной. Очевидно, что любая система  , через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание, будет полной. Действительно, для любой функции f можно взять булеву формулу (по(3.3.) или (3.24.)), и все булевы операции в них заменить формулами над
, через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание, будет полной. Действительно, для любой функции f можно взять булеву формулу (по(3.3.) или (3.24.)), и все булевы операции в них заменить формулами над  , представляющими эти операции. Несложно также доказать утверждение.
, представляющими эти операции. Несложно также доказать утверждение.
Утверждение: если система  - функционально полная и любая
- функционально полная и любая  может быть выражена суперпозицией через функции
может быть выражена суперпозицией через функции  , тогда система
, тогда система  тоже функционально полная.
тоже функционально полная.
В качестве примера рассмотрим системы: 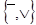 ,
,  ,
,  . Для доказательства функциональной полноты первой системы воспользуемся тем,что система
. Для доказательства функциональной полноты первой системы воспользуемся тем,что система  полная,
полная,  ,
,  ,
, 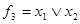 и
и 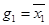 ,
,  .
.
Тогда  ,
,  (т.е. выражена через
(т.е. выражена через  и
и  ), а
), а 