КРАТНЫЕ ИНТЕГРАЛЫ
Двойной интеграл в прямоугольных координатах
Пусть в ограниченной замкнутой области D на плоскости Oxy определена непрерывная функция z = f(x,y). Разобьем область D на n областей с площадями D Si, в каждой из них выберем произвольную точку (xi, yi) и составим интегральную сумму  . Предел этой суммы при неограниченном увеличении числа областей разбиения и при стремлении диаметра наибольшей области max di к нулю называется двойным интегралом от функции z = f(x,y) по области D:
. Предел этой суммы при неограниченном увеличении числа областей разбиения и при стремлении диаметра наибольшей области max di к нулю называется двойным интегралом от функции z = f(x,y) по области D:
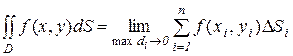 .
.
Элементарная площадь dS в декартовых координатах dS = dxdy`.
Для вычисления двойного интеграла важное значение имеет вид области D.
a) б)

 y y
y y


 y=j2(x) I II
y=j2(x) I II

 d
d
 | |||
 | |||
|

|
 | |||
 | |||
A в x 0 x
Рис. 1.
Если область D может быть задана так, как показано на рис.1.а, двойной интеграл вычисляется по формуле
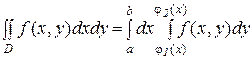 . (1)
. (1)
Если область D имеет вид такой, как показано на рис.1.б, двойной интеграл вычисляется по формуле
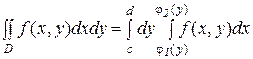 (2)
(2)
В более сложных случаях область D разбивают на простые области типа I и II и пользуются свойством аддитивности двойного интеграла:
если D = D1 + D2, то 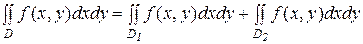 .
.
Двойной интеграл в полярных координатах
Переход от прямоугольных декартовых координат к полярным выполняется по формулам
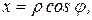
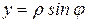 ,
, 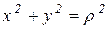 (3)
(3)
при условии, что полюс помещен в начале координат и полярная ось направлена вдоль оси Ox. Элемент площади в полярных координатах имеет вид:
dS = rdrdj.
 |
Рис. 2.
Если область D задана так, как показано на рис.2 (j1 £ j £ j2,, r1(j) £ r £ r2(j)), то переход к полярным координатам в двойном интеграле выполняется по формуле:
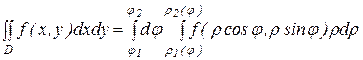 . (4)
. (4)
Если область D охватывает начало координат, в (4) надо положить r1(j) = 0.
Приложения двойных интегралов
Площадь плоской области D на плоскости Oxy вычисляется по формуле:
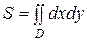 . (5)
. (5)
Если D - плоская пластинка, лежащая в плоскости Oxy, с поверхностной плотностью 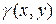 , то массу пластинки находят по формуле
, то массу пластинки находят по формуле
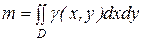 . (6)
. (6)
Пример 1: С помощью двойного интеграла вычислить площадь области, ограниченной линиями y = x2 - 1 и y = 2.
|
 |
-1 0 1 x
Pис. 3.
Спроектируем область D на ось Oy и воспользуемся для вычисления
двойного интеграла формулой (13):
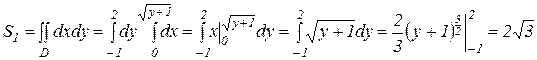 .
.
Тогда площадь всей области D равна S = 2S1 =4 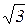 .
.
Ответ: S = 4 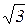 .
.
g
Пример 2. Вычислить площадь плоской области, ограниченной кривой 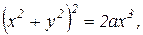
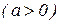 .
.
Решение: Введем полярные координаты (14), тогда уравнение кривой примет вид 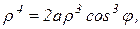 или
или 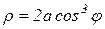 .
.
Область D показана на рис. 4.
 y
y
|

 |
|
Рис. 4.
Эта область симметрична относительно оси, поэтому достаточно вычислить площадь верхней половины области D и результат удвоить. Для верхней половины угол j меняется от 0 до p / 2, а r меняется от 0 до 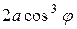 ,
,
поэтомy
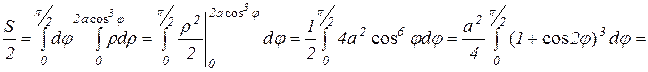
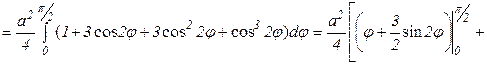
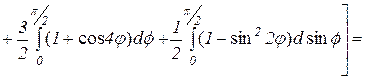
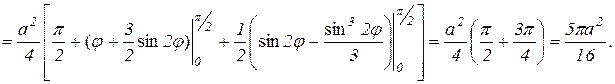

Ответ: Площадь всей области 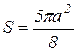 (кв.ед.).
(кв.ед.).
g
Пример 3: С помощью двойного интеграла вычислить массу плоской пластинки, ограниченной линиями 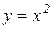 ,
, 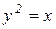 , с заданной плотностью
, с заданной плотностью 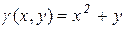 .
.
Решение: Построим область D (рис.6).
 |
D
Рис. 5
Эта область ограничена двумя параболами. Проекцией области на ось Ох является отрезок [ 0; 1 ]. Массу пластинки найдем по формуле (17), вычисляя
двойной интеграл по формуле (1):
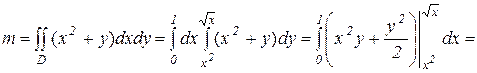
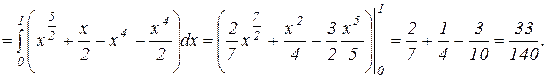
Ответ: 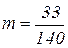 ед. массы.
ед. массы.
g
Пример 4. Вычислить массу плоской пластинки, ограниченной линиями
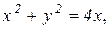
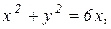
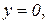
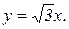
Поверхностная плотность 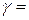
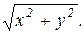

Решение: Построим область D. Уравнение 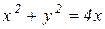 является уравнением окружности
является уравнением окружности 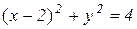 с центром в точке (2; 0) и радиусом 2. Уравнение
с центром в точке (2; 0) и радиусом 2. Уравнение 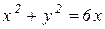 является уравнением окружности
является уравнением окружности 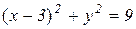 с центром в точке (3; 0) и радиусом 3. Уравнения
с центром в точке (3; 0) и радиусом 3. Уравнения 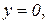
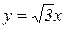 задают прямые линии (см. рис.6).
задают прямые линии (см. рис.6).
При вычислении массы пластинки по формуле (6) перейдем к полярным координатам (3). Тогда уравнения границ области D примут вид:
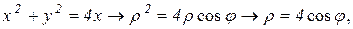
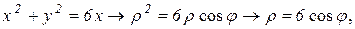
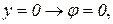
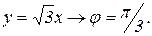
Поверхностная плотность в полярных координатах 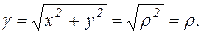


|

|
|
|

|
|

Рис.6
Тогда масса пластинки равна
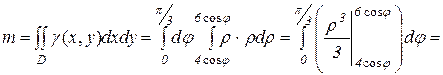
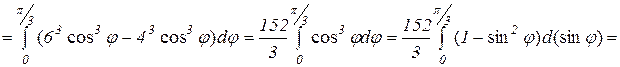

Oтвет: 19 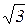 ед. массы.
ед. массы.