Перемещения и деформации. Тензор деформаций

Ни один из существующих в природе материалов не является абсолютно твердым. Под действием внешних сил все тела в боль­шей или меньшей мере меняют свою форму (деформируются). Томки тела меняют свое положение в пространстве непрерывно.

Первоначально непрерывно распределенный материал не содержит после деформации разрывов и пустот (т. е. не воз­никает трещин).

Вектор u имеющий начало в точке А недеформированного тела, а конец – в соответ­ствующей точке A’ дефор­мированного, называется вектором полного перемещения точки (рис. 1.10). Его проек­ции на оси координат

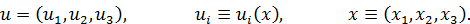
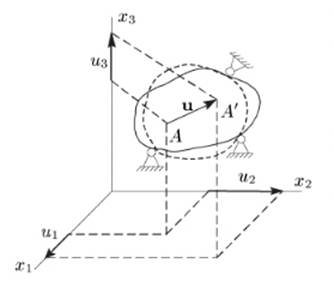
Рис. 1.10

Как правило, в механике деформируемого твердого тела рассматриваются кинематически неизменяемые системы, т. е. не допускающие перемещения тела в пространстве как жестко­го целого. В противном случае in перемещений всех точек ис­ключается составляющая такого переноса. Введенные таким об­разом перемещения для большинства рассматриваемых систем являются малыми по сравнению с геометрическими размерами тела.

Метод определения деформаций заключается в том, что по перемещениям вычисляются изменения длин линейных элемен­тов, а также изменение углов между двумя линейными элемен­тами. Для того чтобы связать перемещения точки А и деформа­ции в ее окрестности, рассмотрим вначале плоскую задачу, т. е. при­мем, что

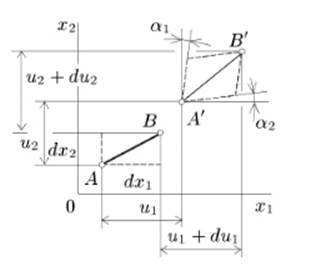
Рис.1.11

В процессе деформации отре­зок AB с проекциями dx₁, dx₂ зай­мет положение A'В' (рис. 1.11). Полное перемещение точки A вдоль оси х₁ есть и₁. Точка В пе­реместится вместе с точкой A на величину u₁ плюс дополнительное перемещение du₁ за счет дефор­мации отрезка вдоль оси х₁.

Так как приращение перемещения мало и du₁ = du₁ х₁, х₂), то с точностью до членов более высокого порядка малости

Здесь первое слагаемое соответствует удлинению составляю­щей dx₁ вдоль оси x₁. Второе слагаемое, в силу малости дефор­маций, описывает перемещение за счет поворота отрезка отно­сительно оси х₂ на угол α₁:

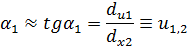
Рассматривая перемещение точки В вдоль оси х₂, по анало­гии получаем

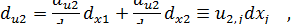
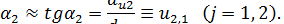
Величины, описывающие линейные удлинения вдоль осей, называются линейными деформациями и обозначаются через

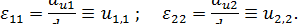
Для описания сдвиговые деформаций используют величину, равную половине суммарного изменения прямого угла между осями координат:

Если деформирование окрестности точки А является про­странственным 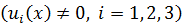, то приращение переме­щения будет

и добавляются деформации

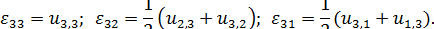
В результате получаем, что в общем случае компоненты де­формации связаны с малыми перемещениями 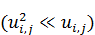фор­мулами, которые называют соотношениями Коти:

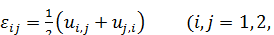(1.27)

Замечание 1. В случае конечных деформаций (геометри­чески нелинейная теория упругости), когда сопоставимы 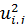и 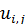компоненты тензора деформаций связаны с перемещени­ями следующими соотношениями:

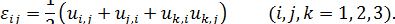
Замечание 2. В задачах изгиба поперечной нагрузкой мембран и тонких пластин могут быть конечными только про­гибы, тогда сопоставимы только 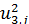и 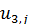. Соотношения связи деформаций с перемещениями принимают вид

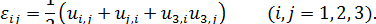
Компоненты деформаций (1.27) образуют тензор второго ран­га, который, как и тензор напряжений, симметричен (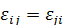). Можно показать, что с его помощью полностью описывается де­формирование произвольного волокна в окрестности рассматри­ваемой точки.