Аппаратура содержит 2000 одинаково сделанных элементов, вероятность отказа каждого из которых равна 0,0005. Какова вероятность того, что откажет аппаратура, если он наступает при отказе хотя бы одного из элементов.
Условие задачи можно рассматривать как последовательность n=2000 независимых испытаний, в каждом из которых вероятность события А– (отказ элемента) постоянна и равна 0,0005.
Событие В, когда отказал хотя бы один элемент, противоположна событию, когда не отказал ни один элемент.
Вероятности, соответствующая тому, что не отказал ни один элемент найдем с помощью формулы Пуассона:
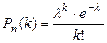 .
.
По условию 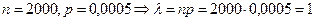 .
.
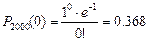
Тогда вероятность искомого события равна:

5.10 2 стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого стрелка при одном выстреле равна –0,6, для второго – 0,7. Дискретная величина Х– число попаданий в мишень. А) Найдите закон распределения Х. б) Найдите вероятность события Х 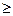 1. в) найдете математическое ожидание М(Х), дисперсию D(Х), среднее квадратическое отклонение σ(Х).
1. в) найдете математическое ожидание М(Х), дисперсию D(Х), среднее квадратическое отклонение σ(Х).
а)Условие задачи соответствует проведению n=2 независимых испытаний. Возможные значения Х таковы: 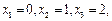 .
.
Пусть событие, состоящее в том, что попал первый стрелок – это событие А1 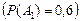 , попал второй стрелок – событие А2
, попал второй стрелок – событие А2 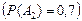 .
.
Тогда
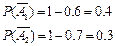
Событие В0, состоящее в том, что ни один стрелок не попал будет произведением трёх несовместных событий 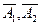 . Т.е.
. Т.е. 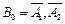 .
.
Т.к. события А1, А2 и 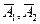 независимы, то искомая вероятность равна:
независимы, то искомая вероятность равна:
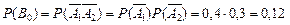
Событие В1, состоящее в том, что только один стрелок попал, будет суммой двух несовместных событий 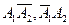 . Т.е.
. Т.е. 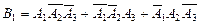 .
.
Т.к. события А1, А2, А3 и 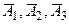 независимы, то искомая вероятность равна:
независимы, то искомая вероятность равна:
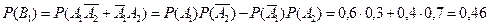
Событие В2, состоящее в том, что два стрелка попадут, будет произведением двух несовместных событий 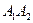 .
.
Т.е. 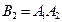 .
.
Т.к. события А1, А2 независимы, то искомая вероятность равна:
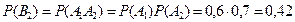
Напишем искомый закон распределения:
| Х | |||
| р | 0,12 | 0,46 | 0,42 |
Б) 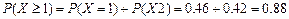
В) Рассчитаем:
1) математическое ожидание
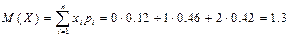
2) дисперсию
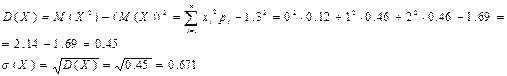
6.10. Автоматический станок производит однотипные изделия, номинальный размер которых равен 3 см. Фактический размер изделий имеет разброс, подчиненный нормальному закону с 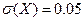 см. Системные отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.
см. Системные отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.
Воспользуемся функцией Лапласа для определения вероятности попадания нормально распределенной случайной величины Х на участок от α до β выражается формулой
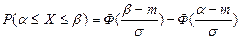
По условию, 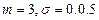
Воспользуемся функцией Лапласа и таблицами значений функции Лапласа. Учитывая, что функция Ф(х) нечетная, то при вычислениях пользуемся свойством: Ф(-х)=-Ф(х).:
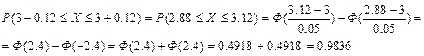
Значит, в среднем будут отбраковываться 100%-98,36%=1,64%
7 Приведённые ниже данные о ценах на 100 видов товаров (в у.е.) записаны в случайном порядке. Используя эти данные необходимо:
1) сделать механическую выборку, отобрав 20 видов товаров (каждого пятого, считая в порядке записи сверху вниз по колонкам и этой выборке);
2) записать эмпирическую функцию распределения;
построить интервальный вариационный ряд с шириной интервала 20 у.е.
4) построить гистограмму частот и эмпирическую кривую распределения;
5) предполагая, что генеральная совокупность имеет нормальное распределение с плотностью f(x). Найти методом моментов по выборке из 1) статистические оценки неизвестных параметров а и σ2;
6) найти доверительные интервалы для а и σ2 с доверительной вероятностью 0,95.
1) Механическая выборка каждого пятого:
2) Запишем элементы выборки в порядке возрастания
Строим эмпирическую функцию распределения:
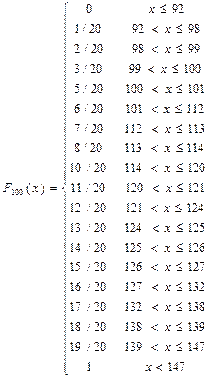
3) Построим интервальный вариационный ряд шириной в 20 у.е.
| Номер, n | Интервалы | Частоты |
| [90;110) | ||
| [110;130) | ||
| [130;150) | ||
4) Построим гистограмму и эмпирическую кривую распределения
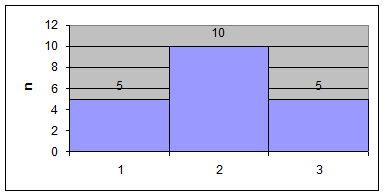
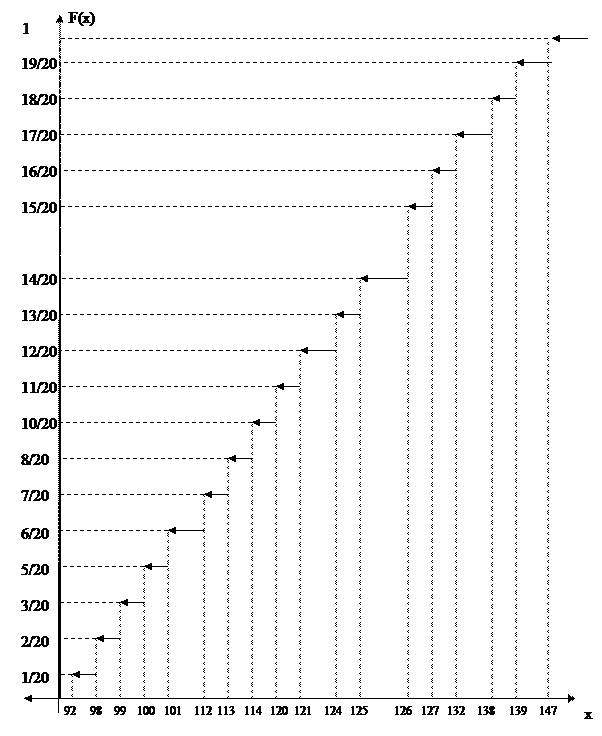
5) Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка:
υ1=М1, μ2=m2.
Учитывая, что υ1=М(Х), μ2=D(Х), 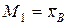 , m2=DB, получим
, m2=DB, получим  , D(X)=DB,
, D(X)=DB,
Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, а дисперсия равна σ2 имеем:
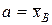 , σ2=DB.
, σ2=DB.
Выборочная средняя равняется 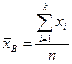
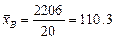 .
.
Выборочная дисперсия равняется 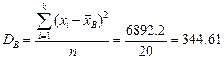
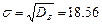
6) Сначала нужно найти «исправленное» квадратическое отклонение s.
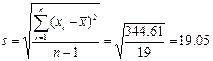
Найдём доверительный интервал для оценки мат. ожидания из формулы 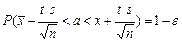
По таблицам распределения Стъюдента с n-1=19 степенями свободы находим t при доверительной вероятности 0,95.
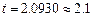
Найдём доверительный интервал:
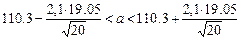
101.36<a<119.24 – доверительный интервал для мат. ожидания.
Найдём доверительный интервал для дисперсии.
Воспользуемся формулой:
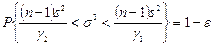
По таблице по данным ε=1-0,95=0,05 и n=19 находим γ1=8,9, γ2=32,8.
Искомый доверительный интервал имеет вид:
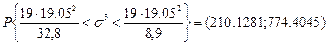
Получить механическую выборку из данных о ценах на товары, приведённых в задаче 7, отобрав 50 товаров (каждый второй, считая в порядке записи сверху вниз по колонкам и этой выборке).
Используя критерий Пирсона, проверить согласие выборочных значений с гипотезой о нормальном распределении генеральной совокупности с параметрами, оценёнными предварительно по выборке.
Оценим параметры распределения, используя метод моментов. Для этого найдем выборочные среднюю и дисперсию:
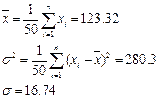
Принимаем эти величины за математическое ожидание и дисперсию величины 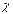 . Таким образом, нужно проверить гипотезу
. Таким образом, нужно проверить гипотезу 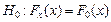 , где
, где 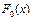 – функция нормального распределения с параметрами (123.32;280.3). Для этого вычислим величину
– функция нормального распределения с параметрами (123.32;280.3). Для этого вычислим величину 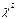 . Разобьем множество значений случайной величины Х на 5 интервалов и подсчитаем число значений, попадающих в каждый интервал.
. Разобьем множество значений случайной величины Х на 5 интервалов и подсчитаем число значений, попадающих в каждый интервал.
| Номер | Интервалы | Частоты |
(- 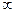 ;98) ;98)
| ||
| [98;112) | ||
| [112;126) | ||
| [126;140) | ||
[140;+ 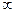 ) )
| ||
Далее вычисляем вероятности попадания СВ Х в каждый интервал:
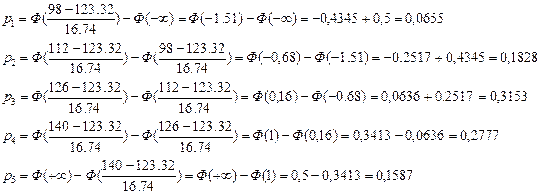
Выборочная статистика 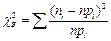 =1.444
=1.444
Число степеней свободы находят по равенству k=S-1-r, где S –число групп, а r – число параметров. В данном случае r=2, а S=5, то k=5-1-2=2.
По таблице критических точек распределения χ2, по уровню значимости α=0,01 и числу степеней свободы находим 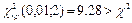 . Значит, принимаем нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. След., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
. Значит, принимаем нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. След., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Получить две механические выборки, объемом по 50 значений, из данных о ценах на товары, приведённых в задаче 7, включая в первую значения, стоящие на нечётных местах, а во вторую – на чётных (нумерация производится по колонкам).
Найти выборочное уравнение линейной регрессии У на Х по результатам двух выборок, считая первую выборку значениями Х, а вторую –У. Проверить гипотезу о значимости коэффициента корреляции.
Имеем две выборки значений X и Y.
Составим расчётную таблицу:
| xi | yi | Xi2 | xiyi |
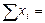 6481 6481
| 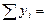 6166 6166
| 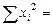 860417 860417
| 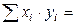 800256 800256
|
Найдём искомые параметры, для чего подставим вычисленные по таблице суммы в соотношения:
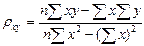
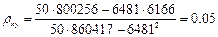
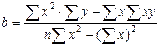
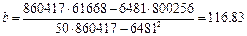
Выборочное уравнение линейной регрессии имеет вид: 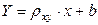 .
.
Т.о. 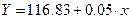 .
.
Теперь найдём выборочный коэффициент корреляции: 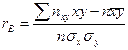 , где x и y – варианты признаков X и Y, nxy – частота пары вариант (х,у), n – объём выборки, σх и σу – выборочные средние квадратические отклонения,
, где x и y – варианты признаков X и Y, nxy – частота пары вариант (х,у), n – объём выборки, σх и σу – выборочные средние квадратические отклонения, 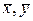 – выборочные средние.
– выборочные средние.
Для любой пары (х,у) их частота nху=1, т. е. каждая пара встречается один раз.
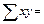 8004175,
8004175, 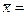 129,62,
129,62, 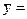 123,32,
123,32, 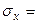 20,17,
20,17, 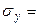 16,74
16,74
Значит 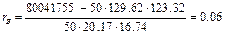 .
.
Коэффициент корреляции отличен от нуля. Возникает необходимость проверить гипотезу о значимости выборочного коэффициента корреляции. Для того, чтобы при заданном уровне значимости α= 0,01 проверить нулевую гипотезу Н0: rГ=0 о равенстве нулю генерального коэффициента корреляции нормальной случайной величины при конкурирующей гипотезе 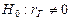 надо вычислить наблюдаемое значение критерия:
надо вычислить наблюдаемое значение критерия:
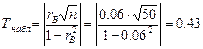
По таблице критических точек распределения Стьюдента, по заданному уровню значимости α=0,01 и числу степеней свободы k=n-2=50-2=48 находим критическую точку tкр(0,01;48)=2,68
Т.к. Тнабл<tкр, то нулевую гипотезу принимаем. Другими словами, выборочный коэффициент корреляции значимо не отличается от нуля, т.е. Х и У не коррелированны.