Одночлен.
Одночленом называют алгебраическое выражение, являющееся произведением букв и чисел. Эти буквы и числа являются множителями данного одночлена. Одночлены или Монономы, проcтой вид математических выражений, прежде всего рассматриваемых и используемых в элементарной алгебре. произведение, состоящее из числового множителя и одной или несколько переменных, взятых каждая с той или другой положительной отметкой степени подразумевается также каждое отдельное число без буквенных множителей. Примеры О.: x*(-3)*y*1*x, 1*a*(-1)*b, a*0*b*(-1/3)*a, 3abc..
Многочлен.
Многочленом называют сумму одночленов. Одночлены, входящие в эту сумму, называют членами многочлена. В математике, многочлены или полиномы от одной переменной — функции вида
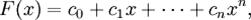
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций. Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
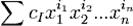 ,
,
где I = (i1,i2,...,in) есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
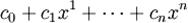
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
R[x1,x2,...,xn].
Например: a2+2ab+b2.
Стандартный вид многочлена.
Говорят, что многочлен имеет стандартный вид, если все его члены записаны в стандартном виде и среди них нет подобных.
Например: 2, a, a-b, a2+2ab2+b2,0.
Многочлен стандартного вида, состоящий из двух членов, называют двучленом; многочлен стандартного вида, состоящий из трёх членов, называют трёхчленом и т. д.
Например:
двучлен: ab-cd, 0,7a2-2b;
трёхчлен: 3a-2b-7, x+yz-2z2;
четырёхчлен: a+b-c-d, -abc-acd-bcd-abd
Любой многочлен можно привести к стандартному виду.
Действия с многочленами.
Сложение (вычитание) многочленов.
Суммой (разностью) двух многочленов называется многочлен, коэффициенты которого являются суммой (разностью) коэффициентов при подобных членах этих многочленов.
На практике для нахождения суммы и разности многочленов используют правила раскрытия скобок, перед которыми стоит знак плюс (знак минус).
Пример:(2x+3y)+(-5x+3y-4)=2x+3y-5x+3y-4=-3x+6y-4; (4x-5y)-(-x-4y)=4x-5y+x+4y=5x-y.
Умножение многочленов.
Чтобы умножить многочлен на одночлен, нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения.
Чтобы умножить многочлен на многочлен, нужно умножить каждый член первого многочлена на каждый член второго многочлена полученные одночлены сложить.
Пример:(-5a)(4-b-a2)=-20a+5ab+5a3;
(2+b)(b2-4)=2b2-8+b3-4b.
Деление многочленов
В алгебре, деление многочленов столбиком — алгоритм деления многочлена f(x) на многочлен g(x), степень которого меньше или равна степени многочлена f(x). Алгоритм представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов f(x) и g(x),  , существуют единственные полиномы q(x) и r(x), такие что
, существуют единственные полиномы q(x) и r(x), такие что
 ,
,
причем r(x) имеет более низкую степень, чем g(x).
Целью алгоритма деления многочленов в столбик является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x).
Пример:
Покажем, что

Частное и остаток от деления могут быть найдены в ходе выполнения следующих шагов:
а. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой 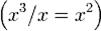 .
.

б. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого  .
.
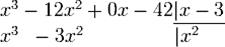
в. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой 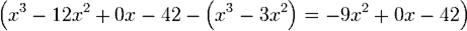 .
.

г. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
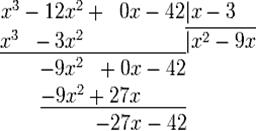
д. Повторяем шаг 4.
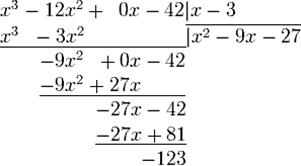
е. Конец алгоритма.
Таким образом, многочлен q(x) = x2 − 9x − 27 — частное деления, а r(x) = − 123 — остаток.
Делимость многочленов
Говорят, что многочлен P(x) делится на многочлен Q(x), если существует многочлен S(x), такой, что P(x) = Q(x)S(x). Многочлен S(x) называется частным от деления P(x) на Q(x). Из (??) следует, что deg S(x) = deg P(x) - degQ(x).
Теория делимости многочленов имеет много общего с теорией делимости целых чисел. В частности, выполняются следующие свойства:
• если P1(x) и P2(x) делятся на Q(x); то P1(x) + P2(x) и P1(x) - P2(x) делятся на Q(x); (3)
• если P(x) делится на Q(x); а T(x) – произвольный многочлен; то P(x)T(x) делится на Q(x); (4)
• если P(x) делится на Q(x); а Q(x) делится на H(x); то P(x) делится на H(x): (5)
Доказательство этих свойств ничем не отличается от доказательства соответствующих свойств делимости целых чисел. Отметим еще некоторые простые свойства:
• если ненулевой многочлен P(x) делится на Q(x); то deg P(x) ≥ degQ(x); (6)
• если deg P(x) = degQ(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны: (7)
(Многочлены называются пропорциональными, если один из них получается из другого умножением на число, отличное от 0.)
Действительно, если P(x) делится на Q(x) и deg P(x) = degQ(x), то частное имеет степень 0, т.е. является числом, отличным от 0. Обратное утверждение очевидно.
Алгоритм Евклида.
4.1 Исторические сведения.
Древнегреческие математики называли этот алгоритм «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике
Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.
Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величин в обеих парах на каждом шаге будут получаться одни и те же неполные частные.
Обобщённый алгоритм Евклида для многочленов.
Рассмотрим пример использования алгоритма Евклида для многочленов.
Найдём наидольший общий делитель многочленов А=x3+3x2+3x+2 и B=x3+2x2+2x+1.
Применим алгоритм Евклида:
| _ | x3+3x2+3x+2 | x3+2x2+2x+1 | ||||
| X3+2x2+2x+1 | ||||||
| _x3+2x2+2x+1 | x2+x+1 | |||||
| x3+ x2+ x | x+1 | |||||
| _x2+x+1 | ||||||
| x2+x+1 | ||||||