Занятие № 2 (2 семестр). Тригонометрические уравнения.
(Обратные тригонометрических функций. Определение функций, их свойства и графики. Простейшие тригонометрические уравнения.)
Обратные тригонометрические функции: свойства и графики.
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс. Приставка «arc » означает обратный.
1. Функция y = arcsin x
Арксинусом числа а называется число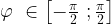 
, такое, что 
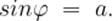Или, можно сказать, что это такой угол 
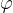, принадлежащий отрезку 
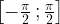, синус которого равен числу а.
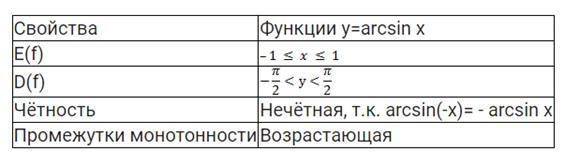
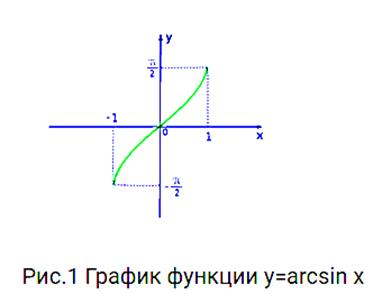
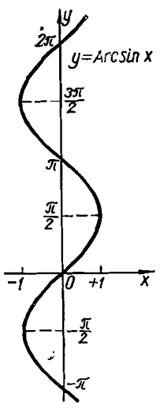
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу (x = sin y).
Определение. Если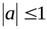 
, то Арксинусом числа α называется такое число из отрезка 
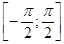, синус которого равен α.
Свойства:
ü sin(arcsin a) = a
ü arcsin(-a)= - arcsin a
Пример.
1. y=аrcsin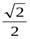 
означает sin y= 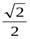поэтому у= π/4
2. arcsin(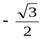
)= – arcsin 
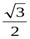= − π/3 т.к sin π/3 =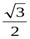
Упражнения с решениями.
Пример 1. Вычислите: а)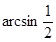 
; б) 
.
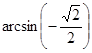Решение. а) Так как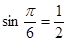 
и 
, то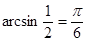 
.
б) Так как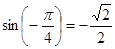 
и 
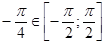, то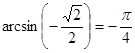 
.
2. Функция y = arccos x
Арккосинусом числа а называется число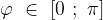 
, такое, что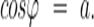 
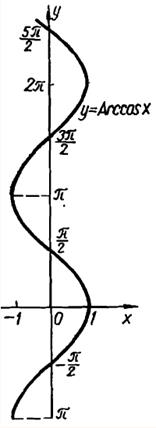
Рассмотрим свойства функции y=arсcos x и построим ее график.
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу (x = cos y).
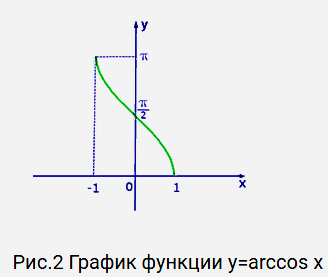
Определение. Если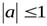 
, то Арккосинусом числа α называется такое число из отрезка 
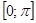, косинус которого равен α.
Свойства:
ü cos(arccos a) = a
ü arccos(-a)= π - arccos a
Пример.
1. arccos1/2 = π/3
2. arccos(-1/2) = π - arccos1/2 = π - π/3 = 2π/3
Упражнения с решениями.
Пример 2. Вычислите: а)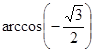 
; б) 
.
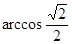Решение. а) Так как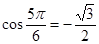 
и 
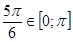, то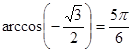 
.
б) Так как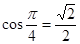 
и 
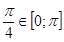, то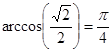 
.
3. Функция y = arctg x
Арктангенсом числа а называется число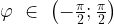 
, такое, что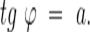 
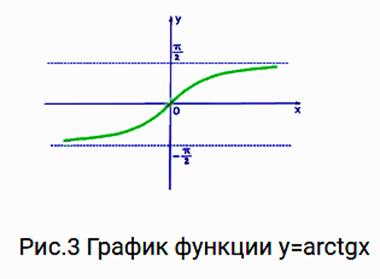
Рассмотрим свойства функции y=arctgx и построим ее график.
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу (x = tg y).
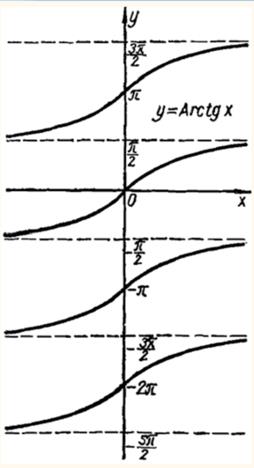
Определение. Арктангенсом числа α называется такое число из интервала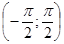 
, тангенс которого равен α.
Свойства:
ü tg(arctg a) = a
ü arctg (-a)= - arctg a
Пример.
1. arc tg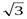 
= π/3
2. arctg (-1)= - arctg 1 = - π/4
Упражнения с решениями.
Пример 3. Вычислите: а)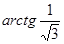 
; б) 
.
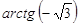Решение. а) Так как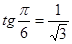 
и 
, то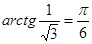 
.
б) Так как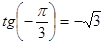 
и 
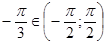, то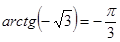 
.
4. Функция y = arсctg x
Арккотангенсом числа а называется число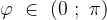 
, такое, что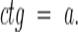 
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу (x = ctg y).
Рассмотрим свойства функции y=arcctgx и построим ее график.
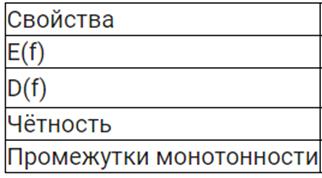
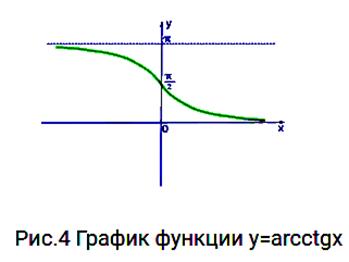
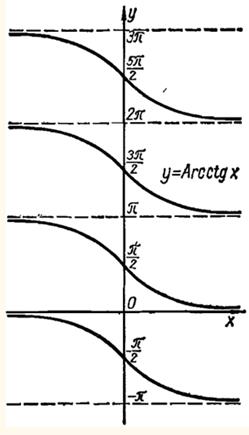
Определение. Арккотангенсом числа α называется такое число из интервала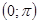 
, котангенс которого равен α.
Свойства:
ü ctg(arcctg a) = a
ü arcctg (-a)= π - arcctg a
Пример.
1. arсc tg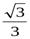 
= π/3
2. arсctg (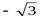
)=π - arсc tg 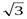= π - π/6= 5π/6
Упражнения с решениями.
Пример 4. Вычислите: а)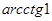 
; б) 
.
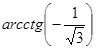Решение. а) Так как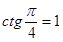 
и 
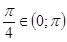, то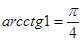 
.
б) Так как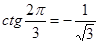 
и 
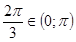, то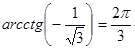 
.
Простейшие тригонометрические уравнения.
2.1. 
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций.
Для решения различных видов тригонометрических уравнений необходимо уметь решать простейшие тригонометрические уравнения. К ним относятся уравнения вида: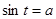 
, 
, 
, 
.
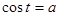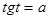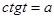Некоторые представления о решении таких уравнений мы уже имеем. Задача нашего урока состоит в следующем: нам необходимо вывести общие формулы для решения простейших тригонометрических уравнений.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента, при котором данная тригонометрическая функция принимает значение а.
Если | а | ≤ 1, то решение этого уравнения определяется формулой:
x = ± arccos а + 2πn, где n = 0; ±1; ±2; ….
Для того, чтобы решить уравнение cos x = а, достаточно найти на единичном кругу или графике соответствующей функции такие точки, абсциссы (ординаты) которых равняются а. Если прямая х = а пересекает единичный круг (график) в точках Мα и Мβ, то углы α и β являются корнями уравнения
cos x = а.
ПРИМЕР 1:
Решите уравнение:
cos x = 0,
РЕШЕНИЕ:
По формуле:
x = ± arccos а + 2 πn
x = ± arccos 0 + 2 πn, k ∈ Z,
или
x = ± π/ 2 + 2 πk, k ∈ Z.
ПРИМЕР 2:
Решите уравнение:
2 cos x = 1,
РЕШЕНИЕ:
Запишем уравнение в следующем виде:
cos x = 1 / 2.
x = ±arccos 1 / 2 + 2 πk, k ∈ Z;
x = ± π/ 3 + 2 πk, k ∈ Z.
ОТВЕТ: ± π/ 3 + 2 πk, k ∈ Z
ПРИМЕР 3:
Решите уравнение:
cos x = –0,2756.
РЕШЕНИЕ:
По формуле:
x = ± arccos а + 2 πn
x = ± arccos (–0,2756) + 2 πn.
ПРИМЕР 4:
Решите уравнение:
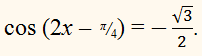
РЕШЕНИЕ:
По формуле:
x = ± arccos а + 2 πn
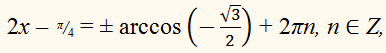
то есть
2 x – π/ 4 = ± 5 / 6 π + 2 πn, n ∈ Z,
откуда
х = π/ 8 ± 5 π / 12 + πn, n ∈ Z.
ОТВЕТ:
π/ 8 ± 5 π / 12 + πn, n ∈ Z
2.2. 
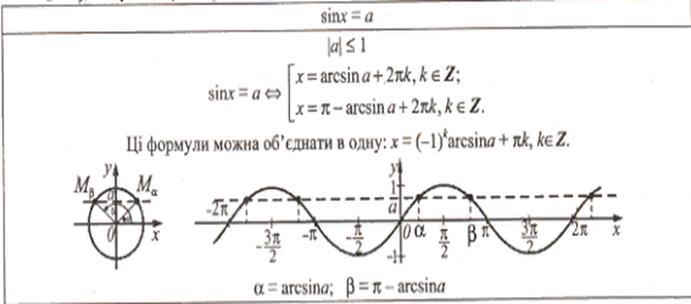
Если | a | ≤ 1, то решение этого уравнения определяется формулой:
x = (–1)n arcsin a + πn, где n = 0; ±1; ±2; ….
Для того, чтобы развязать уравнение sin x = а, достаточно найти на единичном кругу или графике соответствующей функции такие точки, ординаты которых равняются а. Если прямая y = а пересекает единичный круг (график) в точках Мα и Мβ, то углы α и β являются корнями уравнения
sin x = а.
ПРИМЕР 1:
Решите уравнение:
sin x = 1 / 2.
РЕШЕНИЕ:
Используем формулу корней уравнения:
x = (–1) k arcsin a + πk, k ∈ Z.
x = (–1) k arcsin 1 / 2 + πk, k ∈ Z.
x = (–1) k π/ 6 + πk, k ∈ Z.
ОТВЕТ: (–1) k π/ 6 + πk, k ∈ Z
ПРИМЕР 2:
Решите уравнение:
sin x = –1 / 2.
РЕШЕНИЕ:
Используем формулу корней уравнения:
x = (–1) k arcsin a + πk, k ∈ Z.
x = (–1) k arcsin (–1 / 2) + πk, k ∈ Z.
x = (–1) k (– π/ 6) + πk, k ∈ Z,
x = (–1) k+ 1 π/ 6 + πk, k ∈ Z.
ОТВЕТ:
x = (–1) k+ 1 π/ 6 + πk, k ∈ Z
ПРИМЕР 3:
Решите уравнение:
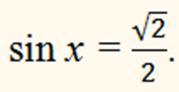
РЕШЕНИЕ:
Используем формулу корней уравнения:
x = (–1) k arcsin a + πk, k ∈ Z.
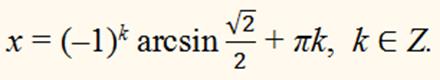
Так как
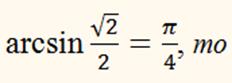
x = (–1) k π/ 4 + πk, k ∈ Z,
ОТВЕТ: (–1) k π/ 4 + πk, k ∈ Z
ПРИМЕР 4:
Решите уравнение:
sin x = 0,932.
РЕШЕНИЕ:
По формуле:
x = (–1) k arcsin a + πk, k ∈ Z
x = (–1) k arcsin (0,932) + πk, k ∈ Z
ПРИМЕР 5:
sin х =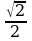 
;
,
;
,
;
,
.
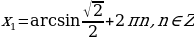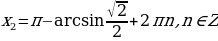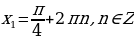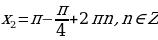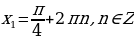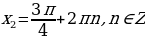Запишем ответ в виде одной серии x = (-1)k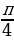 
+ πk, k ϵ Z.
ПРИМЕР 6:
sin х = - ;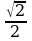
,
;
,
;
,
.
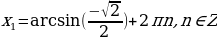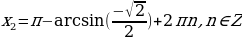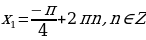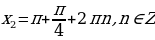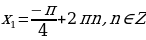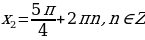Запишем ответ в виде одной серии x = (-1)k (-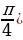 
+ πk, k ϵ Z или
x = (-1)k+1 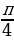+ πk, k ϵ Z.
ПРИМЕР 7:
Решить уравнение
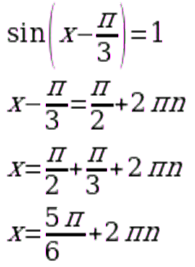
ПРИМЕР 8:
Решить уравнение
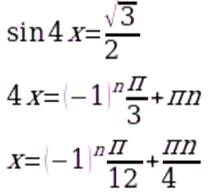
ПРИМЕР 9:
Решите уравнение
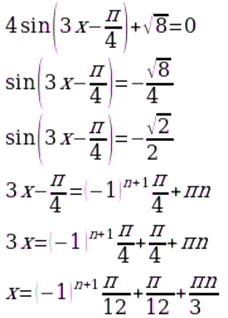
2.3. 
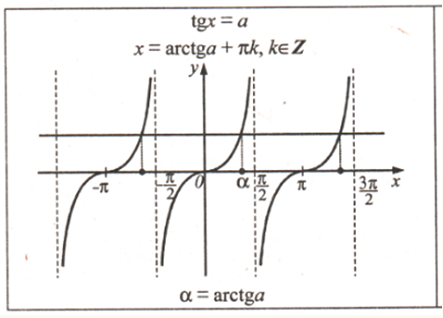
Учитывая периодичность функции у = tg x, получим формулу корней уравнения tg x = а:
x = arctg а + πk, k ∈ Z.
.
Т.о.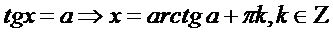 
ПРИМЕР 1:
Решите уравнение:
tg x = √͞͞͞͞͞3.
РЕШЕНИЕ:
По формуле
x = arctg а + πk, k ∈ Z
находим решение:
x = arctg √͞͞͞͞͞3 + πk, k ∈ Z,
так как arctg √͞͞͞͞͞3 = π/ 3,
приходим к окончательному ответу:
x = π/ 3 + πk, k ∈ Z.
ОТВЕТ: π/ 3 + πk, k ∈ Z
ПРИМЕР 2:
Решите уравнение:
tg x = 5,177.
РЕШЕНИЕ:
По формуле
x = arctg а + πk, k ∈ Z
находим решение:
x = arctg 5,177 + πk, k ∈ Z
ПРИМЕР 3:
Решите уравнение:
tg(5 x + π/ 4) = √͞͞͞͞͞3.
РЕШЕНИЕ:
5 x + π/ 4 = arctg √͞͞͞͞͞3 + πk, k ∈ Z,
5 x + π/ 4 = π/ 3 + πk, k ∈ Z,
5 x = π/ 12 + πk, k ∈ Z,
x = π/ 60 + πk/ 5, k ∈ Z.
ОТВЕТ: π/ 60 + πk/ 5, k ∈ Z
2.4. 
Для любого действительного числа а на промежутку (0; π) существует только один угол α такой, что сtg α = а. Это угол
α = arcсtg а + πk, k ∈ Z.
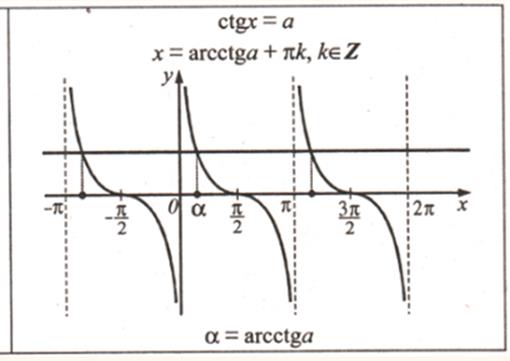
Учитывая периодичность функции у = сtg x, получим формулу корней уравнения сtg x = а:
x = arcctg а + πk, k ∈ Z.
ПРИМЕР 1:
Решите уравнение:
сtg x = √͞͞͞͞͞3.
РЕШЕНИЕ:
По формуле
x = arcсtg а + πk, k ∈ Z
находим решение:
x = arcсtg √͞͞͞͞͞3 + πk, k ∈ Z,
x = π/ 6 + πk, k ∈ Z.
ОТВЕТ: π/ 6 + πk, k ∈ Z
ПРИМЕР 2:
Решите уравнение:
сtg x = 1.
РЕШЕНИЕ:
По формуле
x = arcctg а + πk, k ∈ Z
находим решение:
x = arсctg 1 + πk, k ∈ Z,
x = π/ 4 + πk, k ∈ Z.
ОТВЕТ: π/ 4 + πk, k ∈ Z
ПРИМЕР 3:
Решите уравнение:
сtg x = –√͞͞͞͞͞3.
РЕШЕНИЕ:
Это уравнение равносильно уравнению:
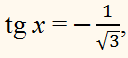
которое решаем с помощью формулы
x = arctg а + πk, k ∈ Z
находим решение:
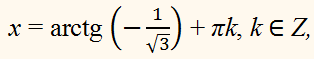
x = – π/ 6 + πk, k ∈ Z.
ОТВЕТ: – π/ 6 + πk, k ∈ Z