2.3.1. Плоскость в пространстве
Пусть плоскость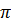 
проходит через точку 
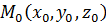и перпендикулярна ненулевому вектору 
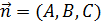. Этими условиями определяется единственная плоскость в пространстве с системой координат 
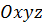. Составим уравнение этой плоскости. Рассмотрим в плоскости 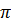произвольную точку 
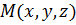. Тогда вектор
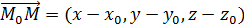
будет принадлежать плоскости 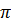, а значит, будет перпендикулярен вектору 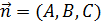. Следовательно, скалярное произведение этих векторов будет равно нулю:
.
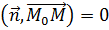Запишем это равенство в координатной форме и получим уравнение
.
Данное уравнение называется уравнением плоскости, проходящей через точку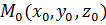 
и перпендикулярно вектору 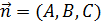. Вектор 
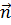называется нормальным вектором плоскости.
В полученном уравнении раскроем скобки и сгруппируем слагаемые:
.
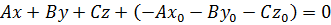Последнее слагаемое, стоящее в скобке обозначим через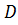 
. Уравнение принимает вид 
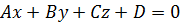. Полученное уравнение называется общим уравнением плоскости. Отметим, что в этом уравнении хотя бы один из коэффициентов 
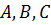отличен от нуля. Можно показать, что любое уравнение первой степени с тремя переменными определяет плоскость.
Общее уравнение плоскости называется полным, если все его коэффициенты отличны от нуля. Если хотя бы один из коэффициентов равен нулю, то уравнение называется неполным. Рассмотрим все возможные виды неполных уравнений:
1) 
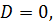при этом уравнение принимает вид 
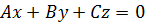, тогда плоскость проходит через начало координат;
2) 
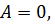
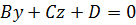, плоскость параллельна оси 
;
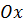3) 
, 
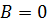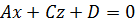, плоскость параллельна оси 
;
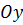4) 
, 
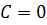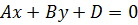, плоскость параллельна оси 
;
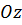5) 
, , 
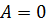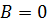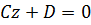, плоскость параллельна плоскости 
;
6) , , 
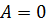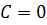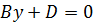, плоскость параллельна плоскости 
;
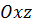7) , , 
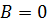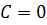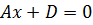, плоскость параллельна плоскости 
;
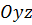8) , , 
, 
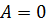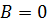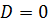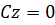, тогда плоскость совпадает с координатной плоскостью ;
9) , , , 
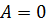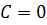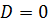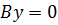, тогда плоскость совпадает с плоскостью ;
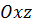10) , , , 
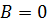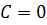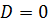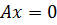, тогда плоскость совпадает с плоскостью .
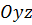Рассмотрим общее уравнение плоскости и выполним преобразования
,
.
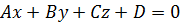
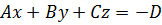
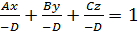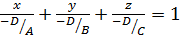Положим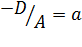 
, 
, 
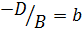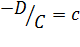. Уравнение принимает вид
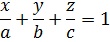
и называется уравнением плоскости в отрезках. Данное уравнение имеет следующий геометрический смысл: модули чисел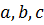 
равны величинам отрезков, которые отсекает плоскость на осях 
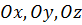от начала координат соответственно.
Пусть даны две плоскости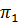 
и 
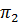, заданные общими уравнениями
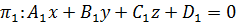
и
.
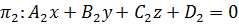Тогда угол между этими плоскостями будет равен углу между их нормальными векторам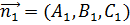и 
и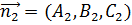 
. Вычислим этот угол с помощью скалярного произведения векторов:
, 
.
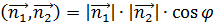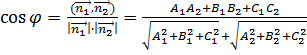Выделим частные случаи:
1) условие параллельности плоскосте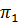й и 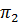эквивалентно условию коллинеарности нормальных векторов 
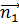и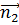 
, а координаты коллинеарных векторов должны быть пропорциональны, то есть
;
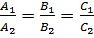2) условие перпендикулярности плоскосте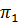й и 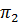эквивалентно условию 
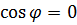или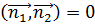 
, то есть
.
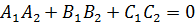2.3.2. Прямая в пространстве
Направляющим вектором прямой называют любой ненулевой вектор, параллельный данной прямой. Выведем уравнение прямой, проходящей через данную точку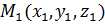 
пространства и имеющей заданный направляющий вектор 
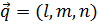. Некоторая точка 
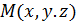будет лежать на данной прямой тогда, и только тогда, когда векторы
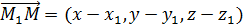и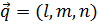
будут коллинеарны, то есть их координаты пропорциональны
.
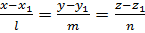Полученные уравнения называется каноническими уравнениями прямой. Обращаем внимание, что в числителях дробей этих уравнений стоят координаты точки, через которую проходит прямая, а в знаменателях – координаты направляющего вектора.
С помощью формулы канонических уравнений прямой можно получить еще одну форму записи прямой, часто используемую при решении задач.
Рассмотрим две точк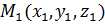и и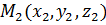 
. Составим уравнение прямой, проходящей через эти точки. Эту прямую можно рассмотреть как прямую, проходящую через точку 
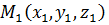и имеющую направляющий вектор 
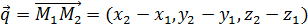. С помощью канонических уравнений получаем
.
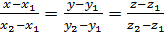Параметрические уравнения прямой получаются из канонических уравнений этой прямой. Примем за параметр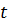 
каждое из соотношений канонических уравнений. Один из знаменателей канонических уравнений отличен от нуля (направляющий вектор прямой отличен от нуля), а соответствующий числитель может принимать какие угодно значения, тогда областью изменения параметра является вся вещественная ось: 
.
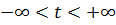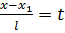, или 
;
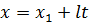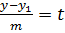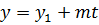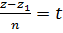, или 
;
, или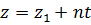 
.
Полученные уравнения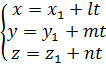 
называются параметрическими уравнениями прямой в пространстве. Такая форма записи уравнения прямой часто используется при решении задач.
Рассмотрим две прямые в пространстве
;
.
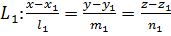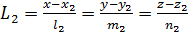Эти прямые могут пересекаться, быть параллельными, скрещиваться. В случаях пересечения или параллельности прямые принадлежат одной плоскости. Установим условия принадлежности двух прямых одной плоскости. Для принадлежности двух прямых одной плоскости необходимым и достаточным условием является условие компланарности трех векторов
,
,
,
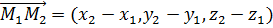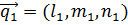а для этого необходимо и достаточно, чтобы смешанное произведение трех этих векторов равнялось нулю. Получаем условие принадлежности двух прямых одной плоскости
.
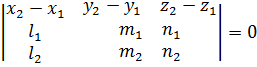Рассмотрим случай, когда прямые пересекаются. В этом случае угол между прямыми будет равен углу между их направляющими векторам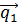и 
и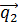 
. Получаем формулу для косинуса угла между двумя прямыми
.
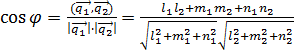В частном случае, когда прямые перпендикулярны, 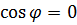. Получается условие перпендикулярности двух прямых пространства
.
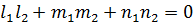В случае, когда прямые параллельны, направляющие векторы 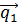и 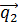коллинеарны, значит, их координаты пропорциональны. Получается условие параллельности двух прямых пространства
.
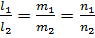(x+2)/(-1)=y/3=(1-z) точка пересечения с плоскостью x ‒ y=2
Параметрический вид ур-я прямой:
подставляем в ур-е плоскости: -t-2