Прежде чем начать изложение результатов, полученных в данном и последующих разделах, приведём ряд известных определений и необходимых обозначений [41-53].
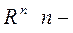мерное вещественное евклидово пространство; в частности при 
получаем двумерное евклидово пространство точек 
где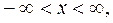 
.
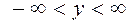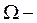открытая область в 
(в частности в 
), через 
обозначим замыкание множества 
;
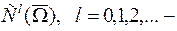множество непрерывных функций, имеющих непрерывные частные производные в до порядка 
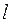включительно; в частности, если 
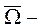область из , то частные производные для некоторой функции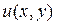 
можно будет записать в виде
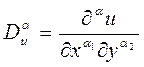, где 
и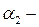 
целые неотрицательные числа.
класс финитных функций из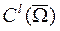 
с носителем ;
множество бесконечно дифференцируемых в функций;
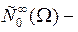класс финитных функций из 
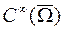с носителем ;
Пусть для определенности область из , а 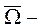ее замыкание.
Определение 1.1.1. Носителем функции 
определенной на множестве называется множество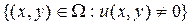 
и обозначается через supp .
Определение 1.1.2. Функция непрерывная в и supp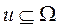 
называется финитной функцией в .
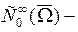множество функций, бесконечно дифференцируемых и финитных в ;
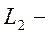гильбертово пространство, состоящее из измеримых по Лебегу на функций, имеющих конечную норму
;
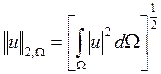пространство функций из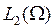 
, имеющих все обобщенные производные по Соболеву до порядка 
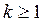включительно, также принадлежащие 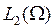с нормой
.
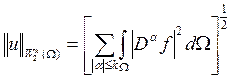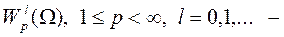пространство функций 
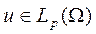, у которых существуют все (обобщенные) производные порядка 
, также принадлежащие 
.
В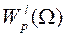 
будет рассматриваться норма
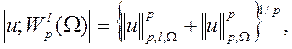
где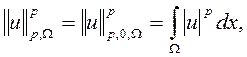 
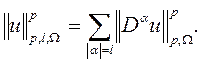
Если А – некоторый оператор, то область определения обозначается через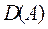 
, область значений через 
.
Определение 1.1.3. Оператор называется взаимнооднозначным, если для любых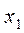 
и 
принадлежащих 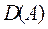из того, что 
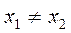следует 
.
Если А отображает 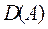на взаимоодназначно, то существует обратное отображение или обратный оператор 
, переводящий на .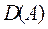
Определение 1.1.4. Оператор А называется замкнутым, если для всякой последовательности 
из того, что 
и 
следует, что 
и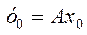 
.
Непосредственно из этого определения следует, что если оператор А незамкнут, то его можно расширить до замкнутого. Эта операция называется замыканием оператора А, а сам оператор называется замыкаемым.
Определение 1.1.5. Оператор А называется вполне непрерывным, если он любое ограниченное множество переводит в компактное множество или что тоже для каждой ограниченной последовательности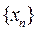 
элементов из 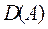последовательность 
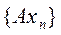содержит сходящуюся подпоследовательность.
Пусть X и Y – нормированные пространства и А ограниченный оператор из X в Y. Определим функционал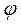 
формулой
(1.1.1)
- сопряженное пространство к пространству Y.
Нетрудно проверить, что 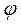- линеен и 
. Итак, каждому 
поставлен в соответствие по формуле (1.1.1) элемент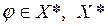 
- пространство сопряженное к X. Таким образом задан линейный непрерывный оператор 
. Оператор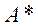 
называется сопряженным к оператору А.
Определение 1.1.6. Оператор А, действующий в гильбертовом пространстве 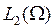называется самосопряжённым, если он симметричен, т.е., если скалярное произведение 
для любых 
и если из тождества
в которых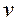 
и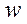 
фиксированы, а 
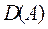– любой элемент из , следует, что 
и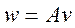 
.
Приведём теперь очень важное понятие спектра и резольвенты оператора.
Если А – линейный оператор в гильбертовом пространстве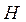 
, то комплексную плоскость 
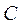можно разбить на две части: резольвентное множество, обозначаемое через 
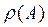и спектр оператора А, обозначаемый через 
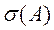, который в свою очередь разбивается на точечный спектр 
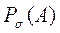и непрерывный 
.
Резольвентное множество 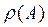состоит из тех 
для которых оператор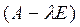 
имеет ограниченный обратный оператор с плотной в 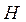областью определения, т.е.
.
Если принадлежит резольвентному множеству, то оператор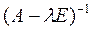 
называется резольвентой оператора А и обозначается 
.
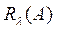Определение 1.1.7. Симметричный оператор А называется положительно определенным, если
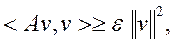для любых 
,
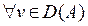где 
Приведем определение понятия k – поперечников по Колмогорову.
Пусть М – центрально-симметрическое подмножество 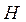( 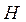- гильбертово пространство), т.е. М=-М.
Величина
называется k – поперечником по Колмогорову множества М, где 
- множество всех подпространств 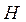, размерности которых не превосходят k.
Определение 1.1.8. Пусть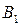 
и 
- банаховы пространства. Говорят, что 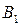вложено в , если 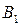является подпространством и существует постоянная c>0 такая, что
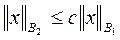при всех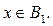 
В данной работе ставятся и исследуются нелинейные уравнения с интегральными «усреднениями». Отметим, что эти уравнения являются нагруженными согласно следующего определения.
Определение 1.1.9. [52] Заданное в области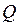 
дифференциальное, интегродифференциальное или функциональное уравнение называется нагруженным, если оно содержит операции взятия следа искомого решения на многообразиях из замыкания 
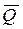размерности строго меньше, чем 
.
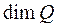1.2 
- оценки решений одного класса вырождающихся эллиптических уравнений