Априорная оценка точности рассчитанных координат

 

Априорная оценка точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации. В качестве основного параметра для априорной оценки точности измеряемых величин применяется средняя квадратическая погрешность измеряемого навигационного параметра m.

Особенностью определения координат является тот факт, что измерения косвенные, то есть измеряются навигационные параметры, и их погрешности затем переносятся в погрешности координат. Рассмотрим процедуру переноса погрешностей измерений в погрешности координат на примере ОМС по двум измерениям.

 

В этом случае линеаризованная система принимает вид:

 

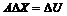(2.21)

 

Так как в измерениях присутствуют погрешности 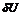, то это приведет к погрешности вектора оценок и система перепишется в виде:

 

, (2.22)

 

Тогда

,

Откуда

(2.23)

 

Формирование ковариационной матрицы погрешности измерений выполняется по формуле

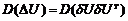, (2.24)

здесь D – обозначение ковариационной матрицы или, что тоже самое,символ дисперсии вектора вектора .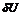

 

Для двумерного случая умножение выглядит так:

 

,

а операция математического ожидания, выполненная над матрицей превращает ее в ковариационную матрицу D:

 

.

 

На главной диагонали D находятся дисперсии измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.

Аналогично определим ковариационную матрицу погрешностей определяемых параметров, используя правила матричного исчисления и ,

получим:

 

 

В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент при D.

И так, ковариационная матрица погрешностей координат N рассчитывается так:

 

(2.25)

 

Для двумерного случая матрица N имеет вид:

,

где n₁₁ - дисперсия погрешностей широты, n₂₂ - дисперсия погрешностей отшествия, n₁₂ = n₂₁ - ковариационные моменты.

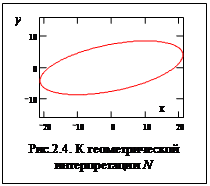
Вся информация о погрешностях содержится в матрице N. В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим связь между элементами матрицы N и параметрами эллипса: полуосями и углом ориентации.

В общем случае такая задача рассматривалась Хоттелингом Г. в 1933 г. и им было показано, что для ковариационной матрицы существуют векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Численно эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гипер - эллипса для n-мерного пространства), необходимо извлечь квадратный корень.

Рассмотрим эту задачу для двумерного случая, то есть для плоскости. Физика и геометрия собственных чисел и векторов заключается в том, что результатом умножения исходной матрицы на собственный вектор будет вектор, коллинеарный собственному, по длине отличаясь в число раз, пропорциональное собственному значению. Математически это запишется так:

 

(2.26)

 

Поставим численный эксперимент, который прояснит этот факт.

Выполним умножение Nz, где в качестве z будем выбирать единичный вектор с направлением Y от 0⁰ до 360⁰. Формирование компонент единичного вектора выполним по формулам:

В качестве примера возьмем матрицу

 

(2.27)

 

В результате перемножения конец вектора p опишет эллипс. (Рис.2.4)

Процедуру умножения матрицы N на z можно рассматривать как оператор, преобразующий единичный вектор z. После перемножения вектор изменит направление и длину. Ниже приведены результаты такого перемножения с дискретностью в один градус, а компоненты вектора p (значения x и y), приведены в таблице 2.1

Табл. 2.1

Y	Y1	x	y	R
	8.13	21.000	3.000	21.213
	8.48	21.049	3.139	21.282
	8.83	21.092	3.277	21.345
	9.18	21.128	3.415	21.402
	9.53	21.158	3.551	21.454
	9.87	21.182	3.686	21.500
	10.22	21.199	3.820	21.540
	10.55	21.209	3.953	21.574
	10.90	21.213	4.084	21.603
	11.24	21.211	4.215	21.625
	11.58	21.202	4.344	21.642
	11.92	21.187	4.471	21.653
	12.26	21.165	4.598	21.658
	12.60	21.137	4.723	21.658
	12.93	21.102	4.846	21.651
	13.27	21.061	4.968	21.639
…	…	…	…	…
	92,48	-0,322	7,432	7,439
	95,38	-0,692	7,358	7,390
	98,30	-1,062	7,281	7,358
	101,24	-1,432	7,201	7,342
	104,19	-1,801	7,120	7,344
	107,13	-2,169	7,037	7,363
	110,05	-2,537	6,951	7,400
	112,94	-2,905	6,863	7,453
	115,78	-3,271	6,773	7,522
	…	…	…	…

В первом столбце таблицы находится направление единичного вектора z, а во втором, направление уже преобразованного вектора - вектора p. В последнем столбце содержится длина R вектора p. Из расчетов, приведенных в таблице видно, что расхождение в направлении вектора z и вектора p величина переменная, но в районе 12⁰ и 102⁰ эти направления совпадают. Кроме того, этим направлениям соответствуют максимальное и минимальное значение длины R. Таким образом, направления собственных векторов 12⁰ и 102⁰ соответственно, они ортогональны. Собственные значения равны приблизительно 21.658 и 7.342 соответственно.

Для двумерного случая можно получить простые формулы для расчета параметров эллипса погрешностей из матрицы N. Опираясь на выражение (2.26), запишем.

n₁₁ z₁ + n₁₂ z₂ = lz₁

n₂₁ z₁ + n₂₂ z₂ = lz₂ (2.28).

или,

(n₁₁-l)z₁ + n₁₂z₂ =0

n₂₁z₁ + (n₂₂-l)z₂ =0

или в матричном виде:

(N - lE) z = 0

где - нулевая матрица.

Формально получаем:

Det(N-lE)Z=adj(N-lE)*0

 

 

следовательно, Det(N-lE)Z= 0.

Так как Z произвольный вектор и, в общем случае не нулевой, то

Det(N-lE)=0

Запишем для двумерного случая:

 

 

(n₁₁ - l) (n₂₂ - l) - n₂₁ n₁₂ = 0

Это квадратное уравнение. Решая его относительно l и, принимая во внимание, что n₂₁ = n₁₂, так как матрица N симметрическая, получим:

 

 

(2.29)

Подставив значения из матрицы (2.27), получим l₁ = 21.659 l₂ = 7.341

Эти значения практически совпали с максимальным и минимальным значением из таблицы.

Определим ориентацию собственных векторов, соответствующих найденным собственным значениям. Считая l известным, подставим это значение в (2.28) и разрешим эту систему относительно z₁ и z₂,учитывая, что z₁ = cos(Y), z₂ = sin(Y).

Первое уравнение системы 2.28 будет выглядеть так:

n₁₁ cos(Y) + n₁₂ sin(Y) = l cos(Y)

 

Разделим первое левую и правую часть на cos(Y).

n₁₁ + n₁₂ tg(Y) = l

Откуда

. (2.30)

(2.31).

Подставив числовые значения, получим Y = 12.388⁰

Таким образом, фактически получено направление большой полуоси эллипса Y относительно норда. Если в (2.31) подставить другое значение l то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.

Для отыскания полуосей необходимо извлечь квадратные корни из собственных чисел.

(2.32)

Когда говорят об оценке точности, то обычно добавляют слова априорная или апостериорная. Априорная - это оценка точности, выполненная по информации о погрешностях измерений полученной ранее. Как правило, такая информация о точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации в каких-то осредненных условиях. Именно такая информация, как правило, содержится в ковариационной матрице погрешностей измерений используемой при расчете координат. В формуле (2.18) она обозначена как D. Если погрешности измерений статистически независимы, то внедиагональные элементы равны нулю и матрица имеет вид:

Именно эти погрешности в соответствии с правилом переноса погрешностей и формируют априорную ковариационную матрицу определяемых параметров.

Процедура построения эллипса погрешностей по ковариационной матрице сводится к следующему:

· Рассчитываем собственные значения l по формуле (2.29)

· Определяем угол ориентации Y по формуле (2.31)

· Рассчитываем полуоси по (2.32)

 

На рис. 2.5 показана связь между элементами ковариационной матрицы и эллипсом. Отрезок, заключенный между касательной к эллипсу параллельной оси Y и самой осью соответствует СКП по широте, или Отрезок на оси Y, отсекаемый вертикальной касательной соответствует СКП по отшествию

На рисунке также показана средняя квадратическая погрешность (СКП) обсервации М, которая рассчитывается, как корень квадратный из следа ковариационной матрицы либо с помощью полуосей эллипса:

 

 

2.5 Апостериорная оценка точности рассчитанных координат

В априорной оценке использовалась информация о точности, полученная по результатам предыдущих измерений, а в апостериорной оценке участвуют текущие измерения, т.е. по которым была вычислена вероятнейшая точка.

Допустим, что ковариационная матрица погрешностей измерений D известна с точностью до постоянного множителя m²:

,

где матрица K известна, а величина m² неизвестна.

Иными словами известны относительные, а не абсолютные значения матрицы D. С учетом этого рассмотрим систему нормальных уравнений:

Подставив вместо D ^-1 выражение получим:

Величина m² (дисперсия наблюдения с единичным весом) сокращается и решение, в итоге, не зависит от абсолютной величины элементов ковариационной матрицы измерений D. Матрицу K ^-1 также называют "весовой" и обозначают через P,а m² - дисперсией наблюдения с единичным весом. Если m² не выносилась из D, то весовой будет просто D ^-1.

Рассмотрим величину

(2.33)

 

Она представляет собой обобщенную (взвешенную) остаточную сумму квадратов уклонений. Здесь M - операция взятия математического ожидания. Упрощенно ее можно рассматривать как отыскание среднего значения.

Рассмотрим выражение в последней скобке, то есть пока без операции взятия математического ожидания:

Последнее слагаемое равно 0. Это вытекает из условия (2.17) и видно из рисунка 2.6: векторы и ортогональны, а скалярное произведение таких векторов равно 0. Тогда .

 

 

Кроме этого:

 

 

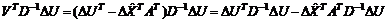
Во втором слагаемом произведение представляет собой правую часть системы нормальных уравнений (2.19), тогда вместо нее запишем левую , тогда окончательно получим:

 

(2.34)

 

По этой формуле можно посчитать значение квадратичного критерия (остаточную сумму квадратов невязок). Здесь D U - вектор, рассчитанный по исходным данным U_o-U_c и первое слагаемое в правой части дает значение остаточной суммы в начальной (счислимой) точке, а второе слагаемое уменьшает это значение за счет смещения к оптимальной точке на величину .

С учетом взятия операции математического ожидания (2.33) справедливо следующее:

 

(2.35)

Распишем первое слагаемое:

 

Правило легко проверяется простым перемножением матриц небольшой размерности.

Распишем второе слагаемое:

 

 

С учетом (2.35) получим:

 

Несмещенная оценка m ² запишется выражением:

Тогда апостериорную оценку ковариационной матрицы погрешности результатов получим следующим

образом:

 

или апостериорная ковариационная матрица погрешностей координат рассчитывается через априорную матрицу так:

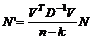(2.36)

Пример. Определить координаты места судна и поправку компаса по измерениям 4-х пеленгов. Расчитать элементы априорного и апостериорного эллипсов погрешностей координат, и средние квадратические погрешности обсервации.

Задачу решить на плоскости в прямоугольных координатах по информации представленной ниже,используя два последовательных приближения.

Окончательный ответ дать в географической системе координат.

Счислимые координаты: x = 8,0 (миль);, y = 4,4 (миль)

 

Координаты ориентиров	Обсервованные пеленги ориентиров	СКП измерения пеленгов
xai	yai	П0	m0
16,3	7,9	25,5	0,2
12,0	9,8	56,6	0,2
5,4	11,8	112,6	0,2
14,2	3,0	350,1	0,2

Решение:

Первая итерация:

1. Записываем навигационную функцию пеленга ()с учетом поправки Z:

1. Рассчитываем производные на счислимые координаты , из которых составляем матрицу A.
2. По навигационной функции рассчитываем счислимые пеленги по счислимым координатам и координатам навигационных ориентиров, полагая поправку Z =0 на первой итерации
3. Вычисляем вектор свободных членов D U, а так же вектор 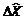и вектор координат ,и ковариационную матрицу погрешностей координат N.

Вычисления приведены ниже:

 

 

Затем из априорной ковариационной матрицы N выбираем верхний левый блок N₁, который определяет точность координат x,y и по формулам (2.26)-(2.29), находим элементы априорного эллипса погрешностей обсервации и СКП М

Элементы априорного эллипса погрешностей обсервации из N’:

a =98,6 м; b =35,6 м; y=139,4⁰; М=104,82 м

Элементы апостериорного эллипса погрешностей обсервации из вернего левого блока матрицы (2.36):

a =149,3 м; b =53,9 м; y=139,4⁰; М=149.30 м

Вторая итерация:

1. Обсервованные коородинаты принимаем за счислимые, т.е. X _c= , и повторяем вычисления по формулам (2.20) и (2.26)-(2.29) с расчетом оценки точности координат.

2. С учетом принятых обозначений, а именно , определяем географические координаты, при известных географических координатах счислимой точки С (j_с, l_с):

j_о= j_с +

l_о=l_с + cos j_m, где j_m = (j_с + j_о)/2 – средняя широта.

 

 

2.6 Графоаналитический расчет

1. На листе миллиметровой бумаги строим систему координат с началом в счислимой точке и выбираем масштаб для прокладки.
2. 
   Производим прокладку линий положения,используя формулу и получаем фигуру погрешностей координат.
3. Определяем приращения координат каждой из вершин фигуры погрешностей D x _ij, D y _ij
4. Каждая точка пересечения двух линий положения О_ij имеет вес, который можно рассчитать по следующе формуле:

, где М_ij – средняя квадратическая погрешность точки по двум линиям положения.

1. Находим средневзвешенное значения приращений координат относительно счислимой точки:

1. Находим обсервованные прямоугольные координаты, используя формулы (2.8), а так же географические координаты по формулам, приведенным во второй итерации.
2. Для сравнения ставим точку по первой итерации на диаграмму графоаналитического расчета.