Определение числового ряда и его сходимости.
Необходимый признак сходимости
Пусть 
– бесконечная последовательность чисел.
Определение. Выражение
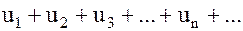, (1)
или, что то же самое, 
, называется числовым рядом, а числа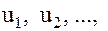 
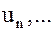– членами ряда. Член 
с произвольным номером называется n -м, или общим членом ряда.
Само по себе выражение (1) никакого определенного числового смысла не имеет, потому что, вычисляя сумму, мы каждый раз имеем дело лишь с конечным числом слагаемых. Определить смысл этого выражения наиболее естественно следующим образом.
Пусть дан ряд (1).
Определение. Сумма n первых членов ряда
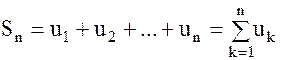
называется n -й частичной суммой ряда. Образуем последовательность частичных сумм:
С неограниченным увеличением числа n в сумме 
учитывается все большее число членов ряда. Поэтому разумно дать такое определение.
Определение. Если при 
существует конечный предел последовательности частичных сумм ряда (1), то ряд называется сходящимся и число 
называется его суммой.
Если последовательность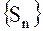 
не стремится к пределу, то ряд называется расходящимся. Отметим, что ряд может расходиться в двух случаях: 1) если 
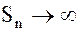, 2) если 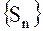колеблющаяся. В обоих случаях говорят, что ряд суммы не имеет.
Пример 1. Рассмотрим ряд, составленный из членов геометрической прогрессии:
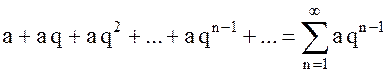, (2)
где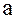 
– называется первым членом прогрессии, а 
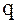– ее знаменателем.
Частичная сумма этого ряда при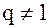 
имеет вид
.
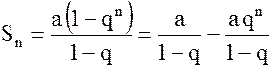Отсюда:
1) если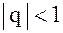 
, то
,
т.е. ряд геометрической прогрессии сходится и его сумма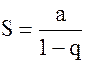 
.
В частности, если 
, ряд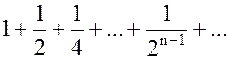 
сходится и его сумма 
.
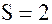При 
ряд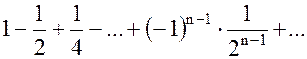 
также сходится и его сумма 
.
2) если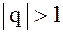 
, то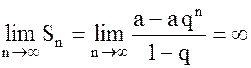 
, т.е. ряд (2) расходится.
3) если 
, то ряд (2) принимает вид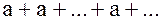 
. В этом случае
и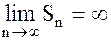 
, т.е. ряд расходится (при 
).
4) если 
, то ряд (2) принимает вид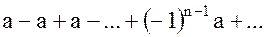 
. Для этого ряд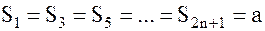а
, а 
,
т.е. 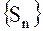является колеблющейся и 
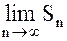не существует, следовательно, ряд также расходится (при ).
Вычисление суммы ряда непосредственно по определению очень неудобно из-за трудности явного вычисления частичных сумм и нахождения предела их последовательности. Но, если установлено, что ряд сходится, его сумму можно вычислить приближенно, т.к. из определения предела последовательности следует, что при достаточно больших 
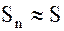. Поэтому при исследовании рядов достаточно
1) знать приемы, позволяющие констатировать сходимость ряда без нахождения его суммы;
2) уметь определить , при котором частичная сумма приближает сумму ряда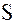 
с определенной точностью.
Сходимость числовых рядов устанавливается с помощью теорем, которые называются признаками сходимости.
Необходимый признак сходимости
Если ряд сходится, то его общий член стремится к нулю, т.е. 
.
Отсюда следует, что если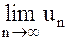 
не равен нулю, то ряд 
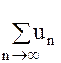расходится.
Пример 2. Доказать, что ряд расходится, если
| а) |  ;
| б) |  ;
|
| в) |  ;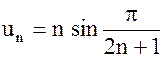
| г) |  .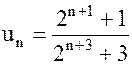
|
Решение.
а)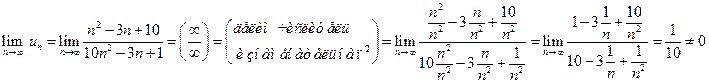 
(методы вычисления пределов последовательностей, см., например, в [5]). Поэтому ряд 
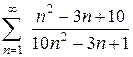расходится.
б) 
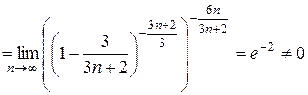
и поэтому ряд расходится. При решении использовался второй замечательный
предел: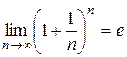 
(подробнее см. [5]).
в)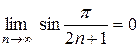 
, т.е. последовательность 
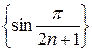– бесконечно
малая. Так как при 
~ 
(см. [5]), то 
~ 
.
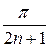Учитывая это, получим:
,
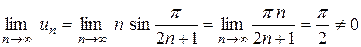значит, ряд расходится.
г) 
,
следовательно, ряд расходится.
Условие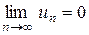 
является необходимым, но не достаточным условием сходимости ряда: существует множество рядов, для которых 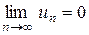, но которые тем не менее расходятся.
Пример 3. Исследовать сходимость ряда 
.
Решение. Заметим, что 
= 
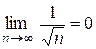, т.е. необходимое условие сходимости выполнено. Частичная сумма
,
 |
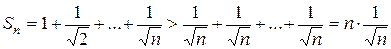– раз
поэтому 
, а это значит, что ряд расходится по определению.
Достаточные признаки сходимости знакоположительных рядов
Пусть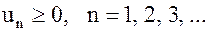 
. Тогда ряд будем называть знакоположительным. Сформулируем некоторые достаточные условия сходимости таких рядов.
Признак сравнения
Пусть 
и 
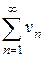– знакоположительные ряды. Если для всех 
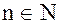выполняется неравенство 
, то из сходимости ряда 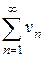следует сходимость ряда , а из расходимости ряда следует расходимость ряда .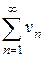
Этот признак остается в силе, если неравенство выполняется не при всех 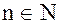, а лишь начиная с некоторого номера 
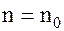. Его можно проинтерпретировать следующим образом: если больший ряд сходится, то меньший тем более сходится; если расходится меньший ряд, то больший также расходится.
Пример 4. Исследовать сходимость ряда , если
| а) |  ;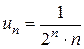
| б) |  ;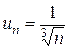
|
Решение.
а) Заметим, что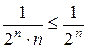 
для всех 
. Ряд с общим членом 
сходится, т.к. является рядом геометрической прогрессии со знаменателем 
(см. пример 1), поэтому данный ряд 
сходится по признаку сравнения.
б) Сравним ряд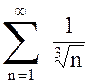 
с рядом 
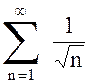. Очевидно, что для всех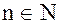 
, поэтому 
. В примере 3 было доказано, что ряд с общим членом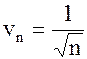 
расходится, значит, данный ряд также расходится.
Несмотря на простоту формулировки признака сравнения, на практике более удобна следующая теорема, являющаяся его следствием.