Лекция № 2
Элементы комбинаторики
План
1 Элементы комбинаторики.
2 Понятие факториала.
3 Перестановки. Размещения. Сочетания.
1 Комбинаторика связана с подсчётом числа комбинаций, которые можно составить из данных элементов, соблюдая те или иные условия.
В качестве примера рассмотрим следующие типы задач.
Пример 1. В соревновании участвуют 8 команд. Сколько существует вариантов распределения мест между ними?
Решение. Обозначим команды цифрами: 1, 2, 3, 4, 5, 6, 7, 8. Тогда возможны, например, такие исходы соревнования: 
, 
, 
.
Выписывать все возможные варианты пришлось бы очень долго. Их, очевидно, столько, сколько существует различных «перестановок» из восьми цифр.
Пример 2. К полуфинальному этапу турнира допущены восемь команд: 1, 2, 3, 4, 5, 6, 7, 8. В финал на равных основаниях попадают лишь три из них. Сколькими способами могут определиться участники финала?
Решение. В этой задаче, в отличие от предыдущей, несущественно, как будет выглядеть вся турнирная таблица; важно лишь, какие команды займут первые три места. Может оказаться, что в финал попадут команды 2, 3, и 5, а может быть 2, 6, и 7 или другие три команды.
При этом порядок расположения в тройке команд-победителей неважен: в финале они всё равно поведут борьбу на равных. Очевидно, что возможных исходов такого соревнования будет столько, сколько существует способов выбора трёх цифр из восьми. При этом порядок расположения выбранных цифр не играет никакой роли: 2, 3, 5 или 5, 3, 2, или 3, 5, 2, – каждый из этих вариантов приведёт к одному и тому же «результату».
Пример 3. Пусть по-прежнему соревнуется восемь команд, но не в полуфинале, а в финале, где разыгрываются три медали: золотая, серебряная, бронзовая. Сколькими способами могут быть распределены медали?
Решение. Как и в предыдущей задаче, здесь придётся рассматривать всевозможные варианты выбора трёх команд из восьми. Но теперь (в отличие от задачи 2) мы вынуждены будем считаться не только с тем, какие именно команды окажутся в тройке команд-победителей, но и с тем, как они поделят места между собой. Поэтому если в задаче 2 распределения 2-3-5 и 5-2-3 первых трёх мест воспринимались как один и тот же «результат», но теперь эти два случая мы будем вынуждены связывать с двумя разными «результатами».
Задачи, в которых производится подсчёт возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
Таким образом, в зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Рассмотрим их отдельно. Однако предварительно познакомимся с понятием факториала.
2 Произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут:
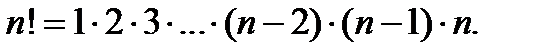
Вычислить:
а) 3!; б) 7!-5!; в) (7!+5!)/6!; г) (6!-4!)/3!; д) (n+1)!/n!.
Размещения
Размещениями из n элементов по m элементам называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.
Число размещений из n по m элементам обозначается символом 
и вычисляется по формуле:
(1)
Перестановки
Перестановками из n элементов называются такие соединения, которые отличаются друг от друга лишь порядком следования элементов.
Число перестановок обозначают символом Pn. Перестановки представляют собой частный случай размещения и вычисляются по формуле:
. (2)
Сочетания
Сочетаниями из n элементов по m называются такие соединения, каждое из которых содержит n элементов, взятых из данных m элементов, и отличается от другого хотя бы одним элементом, обозначается 
и вычисляется о формуле:
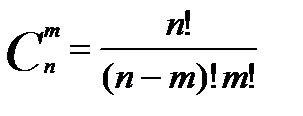или (3)
При решении комбинаторных задач нужно четко представлять, что существует 
способов, чтобы из совокупности n различныхэлементов извлечь без возвращения m штук. (Выбор без возвращения – это такой способ отбора элементов, при котором выбранный элемент не возвращается в исходную совокупность элементов). Исходя из этого, легко заметить, что
, (4)
т.к. выбрать m элементов из n все равно, что решить вопрос, какие n – m элементов оставить в совокупности.
Пример 4. В группе 24 студента. На конференцию нужно выбрать трех представителей. Сколько для этого существует способов?
Решение. Так как порядок, в котором происходит выбор представителей, роли не играет, то количество способов равно:
Следующий пример, встречающийся в различных модификациях, является довольно общим.
Пример 5. Из урны, содержащей M различных белых и N различных черных шаров, нужно извлечь m + n шаров 
, причем так, что среди них точно m белых и n черных. Порядок извлечения шаров роли не играет. Сколько существует для этого способов?
Решение. Так как порядок извлечения шаров не важен, то m белых шаров из M можно извлечь 
способами. Аналогично, n черных шаров из N можно извлечь 
способами. Т.к. каждый из способов извлечения белых шаров можно комбинировать с любыми из способов извлечения черных шаров, то всего способов существует .
Пример 6. Пусть даны пять цифр: 1; 2; 3; 4; 5. Определим сколько трехзначных чисел можно составить из этих цифр.
Решение. Если цифры могут повторяться, то количество трехзначных чисел будет 
.
Если цифры не повторяются, то 
.
Пример 7. В группе из 27 человек нужно выбрать трех делегатов на профсоюзную конференцию. Найдем сколькими способами это можно сделать?
Решение.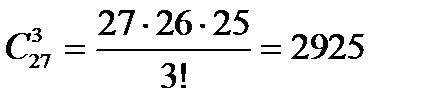 
.
Пример 8. Сколькими способами можно разместить на полке 3 учебника алгебры, 2 учебника геометрии, 1 учебник математического анализа?
Решение. Всего шесть книг.
1) Размещаем учебники по алгебре: 
.
2) Осталось три книги. Размещаем учебники по геометрии: 
.
3) Осталась одна книга. 
.
4) Всего способов размещения: 
.
Пример 9. Сколькими способами можно выбрать конверт с маркой, если имеется 5 видов конвертов и 4 вида марок?
Решение. Выбираем 1 конверт: 
.
Выбираем 1 марку: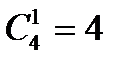 
.
Всего способов 
.
Задания для коллективного решения
1 Сколькими способами из группы, включающей 25 учащихся, можно выбрать актив группы в составе старосты, культорга, физорга?
2 Перед выпуском группа учащихся в 30 человек обменялась фотокарточками. Сколько всего было роздано фотокарточек?
3 Сколькими способами можно рассадить за столом 10 гостей?
4 Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек?
5 Сколькими способами можно рассадить за столом четырёх человек?
6 Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой 1 раз? (120).