Интегрирование (нахождение первообразной) сложной функции
Что необходимо знать для нахождения первообразной сложной функции?
Для нахождения первообразной сложной функции необходимо знать:
- таблицу первообразных основных функций (см. Приложение);
- таблицу производных основных функций (см. Приложение);
- методы нахождения производной сложной функции;
- методы нахождения первообразной сложной функции.
Как отличить сложную функцию от простой?
Простая функция представляет собой некую зависимость переменной (как правило, обозначается «y») от некоторого аргумента (как правило, обозначается «x»). В то же время сложная функция – это такая функция, в которой от аргумента (x) зависит не сама переменная (y), а некоторая вспомогательная переменная (например, u). Тогда простая функция будет иметь вид 
, а сложная – вид 
. Так, например, функция 
является простой, тогда как функция 
– сложной. В первом случае y зависит от x непосредственно через функцию синуса. Во втором же случае y зависит от x через вспомогательную функцию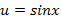 
, которая возведена в квадрат. При этом можно переписать как 
, и эта последняя запись сильно отличается от записи простой функции .
Методы интегрирования сложных функций. Метод подстановки (замены)
Данный метод интегрирования основан на замене какой-либо части сложной функции на переменную (как правило, обозначается t) с последующей подстановкой выражения для дифференциала данной переменной вместо дифференциала исходной переменной. Рассмотрим применение данного метода интегрирования на примере. Найдём первообразную функции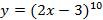 
.
Первый этап – замена внутренней части функции (2x-3) на переменную t. При этом открываются прямые скобки, где в дальнейшем мы будем записывать все этапы замены:
.
Второй этап – нахождение дифференциала новой переменной (dt). Для этого необходимо найти производную первого порядка от левой части записанного в прямых скобках уравнения (2x-3) и помножить её на дифференциал исходной переменной (dx):
.
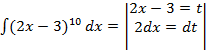Третий этап – нахождение дифференциала исходной переменной (dx) в явном виде. Для этого требуется просто выразить dx из уравнения, полученного на втором этапе:
.
Теперь, когда всё готово к подстановке, мы можем перейти к четвёртому этапу – замене частей исходного интеграла на выражения, записанные в прямых скобках:
.
Константу 
можно вынести за знак интеграла, а значение 
можно найти в таблице первообразных основных функций (см. Приложение). При этом не забываем после нахождения первообразной прибавить к ней константу C, так как интеграл неопределённый:
.
И, наконец, пятый этап, про который никогда нельзя забывать, - необходимо сделать последнюю замену – в последнем выражении подставить вместо t наше исходное выражение (находящееся в уравнении, записанном в прямых скобках на первом этапе):
.
Последнее полученное выражение и будет ответом – первообразной функции 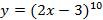. Ответ: 
.
В качестве второго примера возьмём функцию 
и попробуем найти её первообразную с минимумом комментариев:
Замена 
была здесь наиболее целесообразной, поскольку после нахождения дифференциала исходной функции (dx) получившийся 
сократился с уже имевшимся в ней, что позволило избежать нежелательного появления аргумента x под знаком дифференциала dt. Ответ: 
.