Говорят, что множество Х симметрично относительно нуля (симметрично относительно начала координат), если множество Х таково, что (-х) 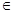 Х для любого х
Х для любого х  Х, т.е. вместе с каждым своим элементом х, оно содержит и ему противоположный элемент (-х).
Х, т.е. вместе с каждым своим элементом х, оно содержит и ему противоположный элемент (-х).
Примеры симметричных относительно нуля множеств:
отрезок [-5;5];
интервал [-3;3];
числовая прямая (-  );
);
Примеры несимметричных множеств:
отрезок [-5;4];
интервал (-2;3);
луч [-10;+  );
);
Несимметричным относительно нуля множеством является и промежуток [-2;2), так как –2 принадлежит этому множеству, а противоположное число 2 ему не принадлежит.
Определение:
Функция у = f(x) называется четной, если:
1) область определения D(f) есть множество, симметричное относительно нуля;
2) для любого х  D(f) выполняется равенство
D(f) выполняется равенство
f(-x) = f(x)
Таким образом, вопрос о четности или нечетности той или иной функции надо рассматривать, учитывая всякий раз не только вид аналитического выражения, но и тот промежуток, на котором определена данная функция. Ответ на вопрос: “Является ли, например, функция у = 1-х  четной функцией?” зависит от выбора области определения. Если указанная функция определена на промежутке, симметричном относительно нуля.
четной функцией?” зависит от выбора области определения. Если указанная функция определена на промежутке, симметричном относительно нуля.
Например, на всей числовой прямой, или на отрезке [-1;1], то в этих случаях функция у = 1-х  является четной функцией. Если же предположим, что область определения есть отрезок [-1;2], то функция у = 1-х
является четной функцией. Если же предположим, что область определения есть отрезок [-1;2], то функция у = 1-х  не является нечетной.
не является нечетной.
Заметим, что наряду с четными и нечетными функциями есть функции, не являющиеся ни теми, ни другими, например, такими являются функции
у=1+sin x; у = 2  ; у =
; у =  .
.
Итак, при исследовании функции у = f(x) на четность или нечетность, необходимо поступать следующим образом:
а) выяснить симметричность области определения функции у = f(x) относительно нуля;
б) если область определения функции не симметрична относительно нуля, то функция не является ни четной, ни нечетной;
в) если область определения функции не симметрична относительно нуля, то необходимо проверить истинность равенств:
f(-x) = f(x) (1)
или f(-x) = f(x) (2) для всех х  D(f)
D(f)
Если выполняется равенство (1), то функция у = f(x) четная; если выполняется равенство (2), то функция у = f(x) нечетная. Если не выполняется ни одно из равенств (1) или (2), то функция не является ни четной, ни нечетной.
Можно предложить следующую блок-схему исследования функций на четность и нечетность:
 | |||
 |
_


 |
+
 |

 +
+
 | |||||
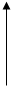 | |||||
 | |||||
_
 | |||
 |
+
 |
Пример: исследовать на четность и нечетность функции:
1) у = 8  ; 2) у =
; 2) у =  ; 3) у =
; 3) у =  ; 4) у =
; 4) у =  .
.
Областью определения функции у = 8  является числовая прямая (-
является числовая прямая (-  ; +
; +  ) – симметричное относительно нуля множество. Далее, имеем f(x) = 8
) – симметричное относительно нуля множество. Далее, имеем f(x) = 8  ;
;
f(-x) = 8  = 8
= 8  . Таким образом, f(-x) = f(x), т.е. функция является чётной.
. Таким образом, f(-x) = f(x), т.е. функция является чётной.
2) Областью определения функции y =  является промежуток (0; +
является промежуток (0; +  ) – не симметричное относительно нуля множество, поэтому функция y =
) – не симметричное относительно нуля множество, поэтому функция y =  не является ни чётной, ни нечётной.
не является ни чётной, ни нечётной.
3) Область определения функции у =  находится из условия
находится из условия 
 или (x – 1)(x + 1)
или (x – 1)(x + 1)  , таким образом, областью определения данной функции является отрезок [-1; 1] – симметричное относительно нуля множество. Далее, имеем
, таким образом, областью определения данной функции является отрезок [-1; 1] – симметричное относительно нуля множество. Далее, имеем
f(x) =  ; f(-x) =
; f(-x) = 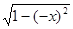 =
=  , т.е. функция у =
, т.е. функция у =  является чётной.
является чётной.
4) Функция у =  не определена при тех значениях x, при которых знаменатель
не определена при тех значениях x, при которых знаменатель 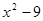 = 0, т.е. в таких точках –3 и3 значит, область определения функции D(f) = (-
= 0, т.е. в таких точках –3 и3 значит, область определения функции D(f) = (-  ; -3)
; -3)  (-3; 3)
(-3; 3)  (3; +
(3; +  ) - симметричное относительно нуля множество. Далее f(x) =
) - симметричное относительно нуля множество. Далее f(x) =  ; f(x) =
; f(x) = 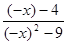 = -
= - 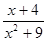 .
.
Так как f(-x)  f(x) и f(-x)
f(x) и f(-x)  -f(x), то функция не является ни чётной, ни нечётной.
-f(x), то функция не является ни чётной, ни нечётной.
Рассмотрим основные свойства чётных и нечётных функций.
Свойство 1. Если y = f(x) и y =  (x) – нечётные функции, то их алгебраическая сумма и разность есть функция нечётная.
(x) – нечётные функции, то их алгебраическая сумма и разность есть функция нечётная.
Доказательство.
Пусть Функции y = (x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму и разность данных функций
(x) имеют область определения X, симметричную относительно нуля. Обозначим сумму и разность данных функций
 (x) и
(x) и  (x) соответственно:
(x) соответственно:
 (x) = f(x) +
(x) = f(x) +  (x);
(x);  = f(x) -
= f(x) -  (x).
(x).
Так как по определению f(-x) = -f(x) и  (-x) = -
(-x) = -  (x), то
(x), то
 (-x) = f(-x) +
(-x) = f(-x) +  (-x) = -f(x) -
(-x) = -f(x) -  (x) = - (f(x) +
(x) = - (f(x) +  (x)) = -
(x)) = -  (x)
(x)
 (-x) = f(-x) -
(-x) = f(-x) -  (-x) = -f(x) +
(-x) = -f(x) +  (x) = - (f(x) -
(x) = - (f(x) -  (x)) = -
(x)) = -  (x).
(x).
Полученные равенства означают, что  (x) и
(x) и  (x) – нечётные функции.
(x) – нечётные функции.
Свойство 2. Если y = f(x) и y =  (x) – нечётные функции, то их произведение и частное есть функция чётная.
(x) – нечётные функции, то их произведение и частное есть функция чётная.
Доказательство
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим произведение и частное данных функций Ф
(x) имеют область определения X, симметричную относительно нуля. Обозначим произведение и частное данных функций Ф  (x) и Ф
(x) и Ф  (x) соответственно:
(x) соответственно:
Ф  (x) = f(x)
(x) = f(x)  (x); Ф
(x); Ф  (x) =
(x) =  (
( (x)
(x)  0).
0).
Учитывая, что функции f(x) и  (x) – нечётные, будем иметь:
(x) – нечётные, будем иметь:
Ф  (-x) = f(-x)
(-x) = f(-x)  (-x) = (-f(x)) (-
(-x) = (-f(x)) (-  (x)) = f(x)
(x)) = f(x)  (x) = Ф
(x) = Ф  (x);
(x);
Ф  (-x) =
(-x) = 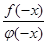 =
=  =
=  = Ф
= Ф  (x).
(x).
Полученные равенства доказывают, что Ф  (x) и Ф
(x) и Ф  (x) функции чётные.
(x) функции чётные.
Свойство 3. Если y = f(x) и y =  (x) – чётные функции, то их сумма, разность, произведение и частное есть функция чётная.
(x) – чётные функции, то их сумма, разность, произведение и частное есть функция чётная.
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму данных функций G
(x) имеют область определения X, симметричную относительно нуля. Обозначим сумму данных функций G  (x),
(x),
разность функций G  (x), произведение функций G
(x), произведение функций G  (x), частное данных функций G
(x), частное данных функций G  (x) соответственно:
(x) соответственно:
G  (x) = f(x) +
(x) = f(x) +  (x); G
(x); G  (x) = f(x) -
(x) = f(x) -  (x); G
(x); G  (x) = f(x)
(x) = f(x)  (x);
(x);
G  (x) =
(x) =  (
(
 0).
0).
Докажем, что G  (x), G
(x), G  (x), G
(x), G  (x), G
(x), G  (x) – чётные функции.
(x) – чётные функции.
Доказательство
Учитывая, что f(x) и  (x) – чётные функции будем иметь:
(x) – чётные функции будем иметь:
G  (-x) = f(-x) +
(-x) = f(-x) +  (-x) = f(x) +
(-x) = f(x) +  (x) = G
(x) = G  (x);
(x);
G  (-x) = f(-x) -
(-x) = f(-x) -  (-x) = f(x) -
(-x) = f(x) -  (x) = G
(x) = G  (x);
(x);
G  (-x) = f(-x)
(-x) = f(-x)  (-x) = f(x)
(-x) = f(x)  (x) = G
(x) = G  (x);
(x);
G  (-x) =
(-x) =  =
= 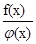 = G
= G  (x).
(x).
Свойство 4. Если y = f(x) – чётная функция, а y =  (x) – нечётная функция, то их произведение является нечётной функцией.
(x) – нечётная функция, то их произведение является нечётной функцией.
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля, причём по определению
(x) имеют область определения X, симметричную относительно нуля, причём по определению
F (-x) = f(x),  (-x) = -
(-x) = -  (x).
(x).
Обозначим произведение данных функций Q(x) = f(x)  (x). Докажем, что Q(x) функция нечётная.
(x). Докажем, что Q(x) функция нечётная.
Доказательство
Учитывая, что f(x) – функция чётная, а  (x) – функция нечётная, будем иметь:
(x) – функция нечётная, будем иметь:
Q(-x) = f(-x)  (-x) = f(x) (-
(-x) = f(x) (-  (x)) = -f(x)
(x)) = -f(x)  (x) = -Q(x).
(x) = -Q(x).
Полученное равенство означает, что функция Q(x) нечётная.
Свойство 5. Всякую функцию, определённую на множестве X, симметричную относительно нуля, можно представить в виде суммы двух функций, каждая из которых определена на том же множестве X и одна из которых чётная, а другая нечётная.
Доказательство
Пусть функция y = f(x) имеет область определения X, симметричную относительно нуля.
Покажем, что существуют функции y =  (x) и y =
(x) и y =  (x), каждая из которых определена на том же множестве X, и они такие, что
(x), каждая из которых определена на том же множестве X, и они такие, что
y =  (x) +
(x) +  (x) = f(x), где y =
(x) = f(x), где y =  (x) – чётная функция, а y =
(x) – чётная функция, а y =  (x) – нечётная функции.
(x) – нечётная функции.
Положим  (x) =
(x) =  ;
;  (x) =
(x) =  .
.
Тогда ясно, что  (x) и
(x) и  (x) определены на множестве X, так как f(x) определена на симметричном относительно нуля множестве X и
(x) определены на множестве X, так как f(x) определена на симметричном относительно нуля множестве X и
 (-x) =
(-x) =  =
=  =
=  (x);
(x);
 (-x) =
(-x) =  =
=  = -
= -  = -
= -  (x);
(x);
 (x) +
(x) +  (x) =
(x) =  +
+  =
=  =
=  =
=
=  f(x),
f(x),
что и требовалось доказать.
Пример. Функцию y = 2  можно представить в виде суммы двух функций y =
можно представить в виде суммы двух функций y =  (x), где
(x), где  (x) =
(x) =  , и y =
, и y =  (x), где
(x), где  (x) =
(x) =  , причём функция y =
, причём функция y =  (x) – чётная, а функция y =
(x) – чётная, а функция y =  (x) – нечётная.
(x) – нечётная.
Многие важные процессы в природе и технике являются периодическими, т.е. повторяющимися по истечении некоторого промежутка времени. Такие периодически повторяющиеся процессы описываются периодическими функциями. Поэтому особенно важно правильное понимание определения периодической функции.
Определение. Функция y = f(x) называется периодической, если существует число 
 0 такое, что выполняются следующие два условия:
0 такое, что выполняются следующие два условия:
1) для любого x из области определения функции y = f(x) числа (x +  ) и (x – T) также входят в область определения и 2) для любого x из области определения выполняется равенство f(x +
) и (x – T) также входят в область определения и 2) для любого x из области определения выполняется равенство f(x +  ) = f(x).
) = f(x).
Число Т называют периодом функции y = f(x).
Замечание. Для периодической функции имеет место равенство
f(x – T) = f(x). Действительно, функция y = f(x) в точке (x – T) определена и
f(x) = f[(x – T) + T] = f(x – T).
Покажем, что если число Т есть период функции y = f(x), то любое из чисел nT, где n 
 , n
, n  0 является периодом этой функции.
0 является периодом этой функции.
Действительно, пусть n = 1, тогда согласно определению и замечанию:
а) точки (x +  ) и (x – T) принадлежат области определения функции y = f(x);
) и (x – T) принадлежат области определения функции y = f(x);
б) f(x) = f(x +  ) и f(x) = f(x – T).
) и f(x) = f(x – T).
Предположим, что для n = k справедливо утверждение точки (x + kT) и (x – kT) принадлежат области определения функции y = f(x). Докажем справедливость этого утверждения при n = k + 1.
По предположению точки (x + kT) и (x – kT) принадлежат области определения функции y = f(x) и Т есть её период. Следовательно, точки
[(x + kT) + T] и [(x – kT) – T], т.е. точки [x + (k + 1)T] и [x - (k + 1)T], принадлежат её области определения.
Итак, для любого x из области определения функции y = f(x) при любом n  Z, n
Z, n  0 точки (x + n
0 точки (x + n  ) и (x – nT) принадлежат области её определения.
) и (x – nT) принадлежат области её определения.
Предположим, что для любого n = k справедливо утверждение
f(x) = f(x + kT) и f(x) = f(x – kT). Докажем справедливость этого утверждения при n = k + 1. Действительно, так как Т является периодом функции y = f(x), то для точки (x + kT) имеем [(x + kT) + T] = f(x + kT), но по предположению
f(x) = f(x + kT) следовательно, f(x) = f[x + (k + 1)T].
Аналогично для точки (x – kT) доказывается, что f(x) = f[x - (k + 1)T], т.е. для любого целого отличного от нуля n утверждение f(x) = f(x + nT) и
f(x) = f(x - nT) доказано.
Число Т называется главным периодом, если оно положительно и является наименьшим среди всех положительных периодов, т.е. из положительных периодов функции y = f(x) (если он существует) называют её основным (главным периодом).
Рассмотрим примеры.
Пример №1. Функция y ={x} ({x} – дробная часть числа х) – периодическая. Заметим, что по определению 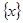 = х – [х], где [x] – целая часть числа х. Область определения данной функции - вся числовая прямая, поэтому для любого действительного числа х и любого T
= х – [х], где [x] – целая часть числа х. Область определения данной функции - вся числовая прямая, поэтому для любого действительного числа х и любого T  x, Т
x, Т  0 числа (х + Т) и (х - Т) принадлежат области определения рассматриваемой функции и f(x +T) = {x+T} = x + T – [x + T] = x + T –([x] + T) = x + T – [x] – T = x – [x] = {x}, где Т
0 числа (х + Т) и (х - Т) принадлежат области определения рассматриваемой функции и f(x +T) = {x+T} = x + T – [x + T] = x + T –([x] + T) = x + T – [x] – T = x – [x] = {x}, где Т  Z, T
Z, T  0.
0.
Таким образом, функция у = {x} – периодическая с периодом Т, где Т  Z, T
Z, T  0.
0.
Наименьшее целое положительное число равно единице. Следовательно, основной период данной функции Т = 1.
Построим график функции у = {x}.
Для этого сначала построим график функции на промежутке х  [0;1), длина которого равна основному периоду функции. Если х
[0;1), длина которого равна основному периоду функции. Если х  [0;1), то {x} = x, то есть на этом промежутке имеем у = х.
[0;1), то {x} = x, то есть на этом промежутке имеем у = х.
Весь график функции у = {x} получим параллельным переносом графика функции у = {x}, где х  [0;1) вдоль оси абсцисс на
[0;1) вдоль оси абсцисс на  = 1.
= 1.
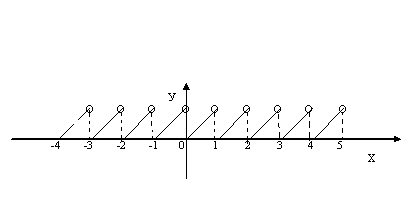
Пример № 2
Функция Дирихле – периодическая с периодом T = r, где r = Q.Действительно,
D(x) = 
D(x + r) = 
Так как r – рациональное число, то сумма х + r - рациональное число, как сумма двух рациональных чисел; с другой стороны, х + r - иррациональное число, как сума иррационального и рационального чисел.
Следовательно, D(x + r) = D(x).
Пример № 3
Функция y = sin  не является периодической, так как, например для числа
не является периодической, так как, например для числа
х = 0 число (х – Т) при Т > 0 или число (х + Т) при Т < 0 не принадлежат области определения данной функции.
Пример № 4
Найти период функции
y = A sin (mx +  ), где А, m,
), где А, m,  - постоянные величины, A
- постоянные величины, A  0, m
0, m  0,
0,
x – аргумент.
Область определения функции – числовая прямая, поэтому числа (х  Т)
Т)  R, где Т
R, где Т  0. Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство
0. Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство
A sin (m (x + T) +  ) = A sin (mx +
) = A sin (mx +  ).
).
Следовательно,
A (sin (m (x + T) +  ) – sin (mx +
) – sin (mx +  ) = 0.
) = 0.
Применяя формулу разности синусов, будем иметь:
2А sin  cos
cos  = 0
= 0
2А sin  cos
cos  = 0
= 0
2А sin  cos
cos  = 0
= 0
2А sin  cos
cos  = 0
= 0
Это произведение должно равняться нулю независимо от значений х.
Так как х - переменная величина, то 2cos 
 0, А
0, А  0 по условию, тогда sin
0 по условию, тогда sin  = 0, откуда следует
= 0, откуда следует
 =
=  , или
, или  , где n
, где n  Z.
Z.
Из множества значений Т наименьшее положительное значение получим при наименьшем положительном значении n = 1, значит период данной функции
 .
.
Заметим, что период функции у = А sin (mx +  ) не зависит от A и
) не зависит от A и  .
.
Аналогично можно найти основные периоды и остальных тригонометрических функций.
Таким образом, функции
y = sin x и y = cos x имеют основной период Т = 2 
у = tg x и у = ctg x имеют основной период Т =  ,
,
а функции у = sin (mx +  ) и у = cos(mx +
) и у = cos(mx +  ) имеют основной период Т =
) имеют основной период Т =  .
.
Функции у = tg (mx +  ) и у = ctg (mx +
) и у = ctg (mx +  ) имеют основной период Т =
) имеют основной период Т =  .
.
 Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.
Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.
Теорема 1. Если периодические функции y = f1 (x) и y = f2 (x), x Î X, имеют один и тот же период T, то их сумма, разность, произведение тоже будут периодическими функциями и число Т будет их периодом.
Доказательство Так как функция y = f1 (x) – периодическая с периодом Т ¹ 0, то для любого x Î X выполняется равенство
f1 (x +Т) = f1 (x) (1)
Так как функция y = f2 (x) – периодическая с периодом Т ¹ 0, то для любого x Î X выполняется равенство
f2 (x +Т) = f2 (x) (2)
Рассмотрим функцию z (x) = f1 (x) ± f2 (x), заданную на множестве X. Тогда для любого x Î X согласно равенствам (1) и (2) будем иметь
z (x +T) = f1 (x +T) ± f2 (x +Т) = f1 (x) ± f2 (x) = Z (x).
Последнее равенство доказывает периодичность функции z (x) представляющей собой сумму или разность двух периодических функций с одним и тем же периодом Т.
Рассмотрим функцию t (x) = f1 (x)×f2 (x), заданную на множестве Х. Тогда для любого x Î X согласно равенствам (1) и (2) будем иметь
t (x +T) = f1 (x +T) ×f2 (x +Т) = f1 (x) ×f2 (x) = t (x).
Данное равенство доказывает периодичность функции t(x) представляющей собой произведение двух периодических функций с одним и тем же периодом Т, причем число Т является периодом как функции t(x), так и функции z(x).
Замечание. Если число Т было наименьшим положительным периодом (т.е. основным периодом) двух заданных функций, то после их сложения или умножения Т может перестать быть наименьшим из положительных периодов.
Пример 5. Функция f1 (x) = 3 sin x + 2 имеет основной период 2p, функция f2 (x) = 2 – 3 sin x имеет основной период 2p, а их сумма
z (x) = f1 (x) +f2 (x) = 3 sin x + 2 + 2 – 3 sin x = 4
наименьшего положительного периода не имеет, так как при любом действительном значении a ¹ 0 z(x+a) = z(x), т.е. любое действительное число является периодом функции z(x), а наименьшего положительного среди действительных чисел нет.
Пример 6. Функция j1(x) = sin x +1 и j2(x) = 1- sin x имеют наименьший положительный период 2p, а для произведения
t(x) = j1(x) × j2(x) = (sin x +1)(1- sin x) = 1- sin2x = cos2x = 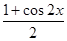
наименьшим положительным периодом есть число p.
Определение Периоды функций Т1 и Т2 называются соизмеримыми, если существуют такие целые отличные от нуля числа m и n, что m×T1 = n×Т2.
Пример 7. Выясним, являются ли соизмеримыми периоды Т1 =  и
и
Т2= 
Решение. Данные периоды будут соизмеримыми, если уравнение  ×m =
×m =  ×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где k Î Z \ {0}. Например, при k = 1 получим
×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где k Î Z \ {0}. Например, при k = 1 получим
 × 15 =
× 15 =  ×4 = 10
×4 = 10
Ответ: Периоды Т1 и Т2 соизмеримы.
Теорема 2. Если периодические функции y = f1(x) и y = f2(x), x Î X, имеют соизмеримые периоды Т1 и Т2 то они имеют общий период.
Доказательство. Так как периоды Т2 и Т2 соизмеримы, то существуют целые отличные от нуля числа m и n такие, что m ×T1 = n × T2 = T ¹ 0. Следовательно, Т – общий период функций y = f1(x) и y = f2 (x). Теорема доказана.
Замечание. По теореме 1 число Т будет также периодом функций
z (x)= f1(x) ± f2 (x), t(x) = f1(x) f2 (x).
Пример 8. Найти период функции
f(x) = sin2x + 3sin(3x-2) -  cos(
cos( x +1).
x +1).
Решение. Так как период синуса равен 2p, функция sin2x имеет период  = p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x-
= p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x-  +
+  ) и ее период равен
) и ее период равен  . Аналогично, функция -
. Аналогично, функция -  cos(
cos( x +1) имеет период
x +1) имеет период  =
=  p.
p.
Для того, чтобы найти общий период функции, представим периоды
Т1 = p; Т2 =  p и Т3 =
p и Т3 =  p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим
p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим
Т1 =  p = 6×
p = 6×  ; Т2 =
; Т2 = 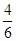 p = 4×
p = 4×  и Т3 =
и Т3 =  p =
p =  ×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60×
×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60×  = 10p – основной период данной функции.
= 10p – основной период данной функции.
Пример 9. Найти период функции y = cos5x-sin2x.
Решение. Функция y = cos5x имеет период T1 =  ; функция y = sin2x – период Т2 =
; функция y = sin2x – период Т2 =  = p. Представим периоды Т1 и Т2 в другом виде: Т1 = 2×
= p. Представим периоды Т1 и Т2 в другом виде: Т1 = 2×  ; Т2 = 5×
; Т2 = 5×  . Таким образом видно, что периоды Т1 и Т2 соизмеримы: 5Т1 = 2Т2, откуда 5×
. Таким образом видно, что периоды Т1 и Т2 соизмеримы: 5Т1 = 2Т2, откуда 5×  = 2×p = 2p. Следовательно, число 2p является периодом данной функции.
= 2×p = 2p. Следовательно, число 2p является периодом данной функции.
Пример 10. Найти основной период функции y = sin2x.
Решение. Понизим степень функции y = sin2x. Тогда y =  =
=
 -
-  cos2x. Период этой функции равен периоду cos2x
cos2x. Период этой функции равен периоду cos2x  = p. Таким образом основной период данной функции равен p.
= p. Таким образом основной период данной функции равен p.
Замечание. Если Т1 и Т2 – основные периоды функций f1(x) и f2(x), то наименьшее положительное число Т, удовлетворяющее условиям:
Т = mT1 = nT2, где m, n Î Z \ {0}, не обязательно является основным периодом функций f1(x) ± f2(x) и f1(x) × f2(x).
Например, основные периоды функций y = cos2x + sinx и y = -sinx равны 2p, а основной период их суммы y = cos2x равен p.
Или, вернемся к примеру 6 и посмотрим на функцию y = sin2x как на произведение функций y = sinx ×sinx. Основной период функции y = sinx есть число 2p, но решая пример 6, мы показали, что основной период функции
y = sin2x равен p.
Заметим, что сложная функция, промежуточным аргументом которой служит периодическая функция, есть функция периодическая, причем периоды этих функций совпадают. Докажем
Теорему 3. Если y = f(j(x)) – сложная функция, где j(x) – периодическая функция с периодом Т, то и сложная функция периодическая с периодом Т.
Доказательство. Так как j(x) – периодическая функция с периодом Т, то для любого действительного x из области определения функции j(x) имеем
j(x + Т) = j(x),
тогда для функции y = f(j(x)) при любом действительном х из области определения функции j(x) будем иметь
j(x + Т) = f (j(x)) = f(j(x)) = y(x).
Последнее равенство доказывает, что функция y = f(j(x)) периодическая с периодом Т.
Пример 11. Функция y = cos3x периодическая с периодом  = p. В силу теоремы 3 функция y = 5cos22x +
= p. В силу теоремы 3 функция y = 5cos22x +  +3 периодическая с периодом p.
+3 периодическая с периодом p.
Рассмотрим примеры на доказательство периодичности или не периодичности функций.
Пример 12. Доказать, что функция y = sin 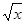 не является периодической.
не является периодической.
Доказательство. I способ: D(y) = [0;+¥). Пусть положительное число
Т – период данной функции, тогда должно выполнятся условие (х-Т) Î D(y), для любого x Î D(y). Но при x = 0 (х-Т) Ï D(y), следовательно, T > 0 не является периодом функции.
Докажем, что Т < 0 не может быть периодом функции y = sin  .
.
Если T < 0 – период данной функции, то должно выполнятся условие (х + Т) Î D(y) для любого x Î D(y). Но при x = 0 (х + Т) Ï D(y), следовательно, T < 0 не является периодом функции.
II способ: Предположим, что функция y = sin 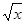 имеет период, равный Т. Тогда y = sin
имеет период, равный Т. Тогда y = sin  = y = sin
= y = sin 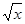 при любом действительном x Î D(y). При x = 0 будем иметь, что sin
при любом действительном x Î D(y). При x = 0 будем иметь, что sin  = sin 0 = 0. Значит
= sin 0 = 0. Значит
 = pn, (1)
= pn, (1)
а при x = T получим sin  = sin
= sin  = 0. Следовательно,
= 0. Следовательно,
sin  = pk. (2)
= pk. (2)
Разделив почленно (2) на (1) при n ¹ 0, получим  =
= 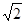 =
=  , чего не может быть, так как
, чего не может быть, так как  число иррациональное.
число иррациональное.
Пример 13. Доказать, что функция y = cos2 x не является периодической.
Доказательство. Пусть данная функция имеет период Т ¹ 0. Тогда для любого x Î D(y) (D(y) = R) должно выполнятся равенство
cos (x+T)2 = cos x2 или
cos (x+T)2 - cos x2 = 0
Преобразуем данное равенство по формуле разности косинусов, получим
2 sin 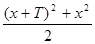 × sin
× sin 
2sin (x2 + T×x +  ) × sin (T×x +
) × sin (T×x +  ) = o
) = o
Это произведение должно равняться нулю независимо от значений переменной величины x, а это невозможно, sin (T×x +  ) ¹ o и
) ¹ o и
sin (x2 + T×x +  ) ¹ 0. Значит допущение, что функция y = cos2 x периодическая неверно, т.е. данная функция не является периодической.
) ¹ 0. Значит допущение, что функция y = cos2 x периодическая неверно, т.е. данная функция не является периодической.
Пример 14. Доказать, что функция y = |sin (x)| является периодической с периодом p.
Доказательство. D(y) = R. Пусть периодом данной функции будет число Т ¹ 0. Тогда
|sin (x + Т)| = |sin (x)| (3)
Это равенство будет выполнятся в двух случаях:
1) sin (x + Т) = sin (x) и тогда
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-06-03 Нарушение авторских прав и Нарушение персональных данных