Пусть существует функция Ляпунова  такая, что
такая, что
 ,
,  .
.
Тогда тривиальное решение уравнения (В.8) равномерно асимптотически устойчиво. Здесь 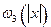 ̶ скалярная, неубывающая, положительно определенная функция.
̶ скалярная, неубывающая, положительно определенная функция.
Векторные функции Ляпунова. Для решения вопроса об устойчивости сложных или составных систем удобно использовать векторные функции Ляпунова. Впервые векторные функции Ляпунова для исследования устойчивости рассмотрели Р. Беллман [74] и В.М. Матросов [48]. Р. Беллман исследовал систему, состоящую из двух подсистем. Ф.Н. Бейли [71] обобщил предложенный Р. Беллманом метод на более сложные системы.
Рассмотрим систему, которая после декомпозиции описывается уравнениями
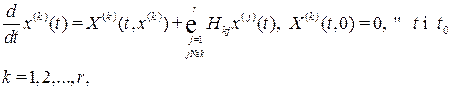 (В.10)
(В.10)
где 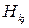 − числовая
− числовая  -матрица. Если пренебречь взаимосвязями, то получим
-матрица. Если пренебречь взаимосвязями, то получим 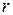 независимых подсистем
независимых подсистем  , которые описываются уравнениями
, которые описываются уравнениями
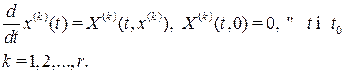 (В.11)
(В.11)
Пусть каждая из этих подсистем обладает функцией Ляпунова  , которая обладает следующими свойствами
, которая обладает следующими свойствами
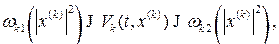 (В.12)
(В.12)
 (В.13)
(В.13)
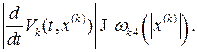 (В.14)
(В.14)
Функции  скалярные, неубывающие, положительно определенные при
скалярные, неубывающие, положительно определенные при 
В (В.13)  являются производными по времени в силу системы уравнений (В.11). Так как эти производные отрицательно определенные, подсистемы
являются производными по времени в силу системы уравнений (В.11). Так как эти производные отрицательно определенные, подсистемы  асимптотически устойчивы. Кроме того, в силу (В.12) функции
асимптотически устойчивы. Кроме того, в силу (В.12) функции  имеют бесконечно большой нижний предел. Поэтому подсистемы
имеют бесконечно большой нижний предел. Поэтому подсистемы  асимптотически устойчивы в целом. В случае, когда подсистемы являются линейными стационарными, имеет место экспоненциальная устойчивость.
асимптотически устойчивы в целом. В случае, когда подсистемы являются линейными стационарными, имеет место экспоненциальная устойчивость.
Теорема 4. Пусть подсистема (В.11) обладает функциями Ляпунова 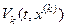 , удовлетворяющими соотношениями (В.12)-(В.14), и элементы матрицы
, удовлетворяющими соотношениями (В.12)-(В.14), и элементы матрицы  , составленные из констант
, составленные из констант  , входящих в уравнения (В.12)-(В.14), и евклидовых норм
, входящих в уравнения (В.12)-(В.14), и евклидовых норм 
матриц взаимосвязи 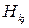 из (В.10), имеют вид
из (В.10), имеют вид

Тогда если положение равновесия 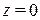 системы
системы
 (В.15)
(В.15)
асимптотически устойчиво, то положение равновесия

агрегированной системы (В.10) асимптотически устойчиво.
Система (В.15) является системой сравнения для агрегированной системы (В.10). С ее помощью исследование устойчивости системы (В.10)  -порядка
-порядка  сводится к исследованию устойчивости линейной стационарной системы
сводится к исследованию устойчивости линейной стационарной системы 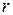 -го порядка.
-го порядка.
Устойчивость по первому приближению. В приложениях устойчивость решений часто исследуется по так называемым «уравнениям первого приближения» [26]. Пусть требуется исследовать на устойчивость решение 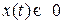 системы
системы
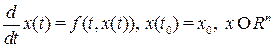 , (В.16)
, (В.16)
где 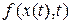 − некоторая дифференцируемая функция. Линеаризуем уравнение (В.16) в окрестности решения
− некоторая дифференцируемая функция. Линеаризуем уравнение (В.16) в окрестности решения 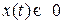 . Для этого запишем в виде
. Для этого запишем в виде
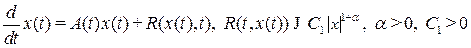 .(B.17)
.(B.17)
Наряду с (В.17) рассмотрим линейную систему
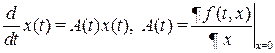 . (В.18)
. (В.18)
Система (В.18) называется системой первого приближения для (В.17). Далее изучают устойчивость уравнения (В.18) и по нему судят об устойчивости нелинейной системы (В.16). Такой прием без должного обоснования применялся задолго до Ляпунова. Ляпунов первым установил, когда это является правомерным, а когда нет.
Предположим, что уравнение первого приближения (В.18) является стационарным, т.е.
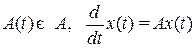 .
.
Теорема 5. (А.М. Ляпунов).
Пусть тривиальное решение системы
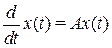 (В.19)
(В.19)
асимптотически устойчиво. Тогда тривиальное решение нелинейной системы (В.17) также асимптотически устойчиво.
Доказательство. Обозначим через 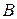 решение уравнения
решение уравнения  , где
, где  − единичная матрица. Введем функцию Ляпунова
− единичная матрица. Введем функцию Ляпунова  и найдем ее производную в силу системы (В.19)
и найдем ее производную в силу системы (В.19)
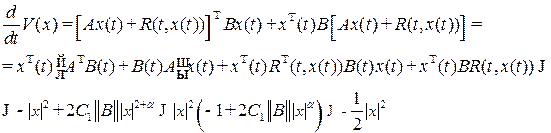 для столь малых
для столь малых  , что
, что
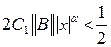 . (В.20)
. (В.20)
Таким образом, функция удовлетворяет теореме 3 об асимптотической устойчивости и, таким образом, тривиальное решение уравнения (В.17) асимптотически устойчиво.
■
Замечание. Отметим, что области притяжения уравнений (В.17) и (В.18) не совпадают. Если для (В.18) областью притяжения является все пространство 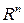 , то для (В.17) можно гарантировать, что
, то для (В.17) можно гарантировать, что 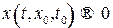 лишь для состояний, удовлетворяющих оценке (В.20).
лишь для состояний, удовлетворяющих оценке (В.20).
Пример 2.
Исследовать положение равновесия  автономной системы
автономной системы

Рассмотрим соответствующую систему первого приближения
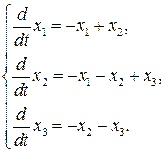
Ей соответствует матрица  с собственными значениями
с собственными значениями 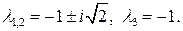 Линейная система асимптотически устойчива, так как
Линейная система асимптотически устойчива, так как  . Тогда, по теореме 5, исходная система асимптотически устойчива.
. Тогда, по теореме 5, исходная система асимптотически устойчива.
□
Теорема 6. (А.М. Ляпунов).
Если тривиальное решение системы первого приближения (В.18) неустойчиво, то тривиальное решение нелинейной системы (В.17) также неустойчиво.
Пример 3.
Показать, что положение равновесия  системы
системы

является неустойчивым.
Запишем систему первого приближения
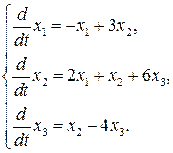
Ей соответствует матрица  , собственные значения которой равны
, собственные значения которой равны  Отметим, что
Отметим, что  , т.е. существует собственное значение, у которого вещественная часть положительна. Значит, линейная система неустойчива. По теореме 6 исходная нелинейная система тоже неустойчива.
, т.е. существует собственное значение, у которого вещественная часть положительна. Значит, линейная система неустойчива. По теореме 6 исходная нелинейная система тоже неустойчива.
□
Случаи, рассмотренные в теоремах 5 и 6, называются некритическими. В некритических случаях матрица  не имеет собственных значений на мнимой оси. В этих случаях характер устойчивости полной нелинейной системы совпадает с характером устойчивости системы первого приближения независимо от вида нелинейных членов.
не имеет собственных значений на мнимой оси. В этих случаях характер устойчивости полной нелинейной системы совпадает с характером устойчивости системы первого приближения независимо от вида нелинейных членов.
Случаи, когда матрица 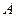 имеет собственные значения на мнимой оси, называют критическими или маргинальной устойчивостью. В критических случаях устойчивость или неустойчивость зависит от вида нелинейных членов.
имеет собственные значения на мнимой оси, называют критическими или маргинальной устойчивостью. В критических случаях устойчивость или неустойчивость зависит от вида нелинейных членов.
Пример 4.
Исследовать на устойчивость положение равновесия  системы
системы

Система первого приближения имеет вид
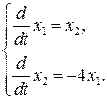
Собственные значения матрицы  этой системы равны
этой системы равны  . Оба собственных значения лежат на мнимой оси, что соответствует случаю маргинальной устойчивости.
. Оба собственных значения лежат на мнимой оси, что соответствует случаю маргинальной устойчивости.
Построим функцию Ляпунова для исходной системы. Напомним, что  . Пусть
. Пусть  , где скаляр
, где скаляр  неизвестен.
неизвестен.
Производная в силу системы
 .
.
Для отрицательной определенности  достаточно, чтобы
достаточно, чтобы  т.е.
т.е.  Полученная производная в силу системы
Полученная производная в силу системы 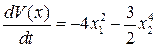 является отрицательно определенной, а сама функция Ляпунова
является отрицательно определенной, а сама функция Ляпунова 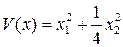 положительно определена. Значит, нелинейная система устойчива.
положительно определена. Значит, нелинейная система устойчива.
□
Понятия «наблюдаемость», «управляемость», «устойчивость» являются структурными (внутренними) свойствами системы, т.е. сохраняются при всех эквивалентных преобразованиях системы.
Существенным элементом формулировки задачи управления, наряду с построением математической модели объекта управления (В.4) и определения ограничений на фазовые траектории  и управляющие воздействия
и управляющие воздействия  , является формирование цели управления, а также построения функционала, «измеряющего» эффективность управляющих воздействий.
, является формирование цели управления, а также построения функционала, «измеряющего» эффективность управляющих воздействий.
Предположим, что векторы  и
и  могут изменяться в некоторых допустимых областях:
могут изменяться в некоторых допустимых областях:
 (В.21)
(В.21)
Рассмотрим типичные случаи задания ограничений на управляющие воздействия. Для этого напомним сначала некоторые определения из теории множеств.
Определение 10. Открытым называют множество, каждый элемент которого входит в него с некоторой окрестностью. Замкнутым множеством называют дополнение к открытому.
Определение 11. Пусть 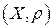 ̶ метрическое пространство.
̶ метрическое пространство.  называют ограниченным, если оно содержится в некотором шаре
называют ограниченным, если оно содержится в некотором шаре 
Определение 12. Выпуклым называют множество, в котором все точки отрезка, концами которого являются любыми две точки этого множества, также принадлежат этому множеству.
Предположим, что для каждого  задано подмножество
задано подмножество  (обычно замкнутое, ограниченное и выпуклое или все
(обычно замкнутое, ограниченное и выпуклое или все 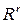 ). Обозначим набор всех подмножеств
). Обозначим набор всех подмножеств 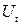 через
через 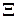 , т.е.
, т.е. 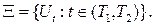
Определение 13. 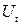 называют областью ограничений при
называют областью ограничений при  , и
, и  – множеством ограничений. Если
– множеством ограничений. Если 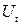 – множество всех ограниченных кусочно непрерывных функций
– множество всех ограниченных кусочно непрерывных функций  из
из  , то говорят, что
, то говорят, что 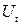 есть множество или область управлений, удовлетворяющих ограничениям
есть множество или область управлений, удовлетворяющих ограничениям 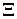 .
.
Пример 5.
Пусть 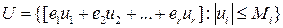 , где
, где 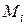 – заданные постоянные и
– заданные постоянные и 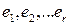 – стандартный базис в
– стандартный базис в 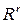 . При
. При  ограничивающим множеством является гиперкуб.
ограничивающим множеством является гиперкуб.
□
Пример 6.
Пример ограничений, зависящих от времени:

Здесь  .
.
□
Пример 7.
Ограничения на управление имеют вид  где М – заданное число,
где М – заданное число,  ̶ евклидова норма. Ограничивающим множеством является гиперкуб.
̶ евклидова норма. Ограничивающим множеством является гиперкуб.
□
Следует отметить, что в ряде случаев можно перейти к открытой области изменений управляющих воздействий. Эта операция состоит в замене вектора  функцией другого вектора
функцией другого вектора 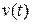 , не ограниченного. Геометрически эта операция отображает область
, не ограниченного. Геометрически эта операция отображает область  во все
во все 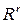 .
.
Сформулируем задачу управления объектом
 ,
,  (В.22)
(В.22)
Пусть 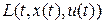 – непрерывная действительная функция, заданная на
– непрерывная действительная функция, заданная на 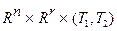 , т.е. непрерывная функция вида
, т.е. непрерывная функция вида
 ,
,
и 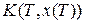 − действительная функция на
− действительная функция на  , где
, где 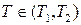 :
:
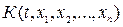 .
.
Будем считать подмножество  из
из 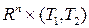 заданным и назовем его множеством цели (target set). Элементами множества целей являются пары
заданным и назовем его множеством цели (target set). Элементами множества целей являются пары 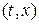 , состоящее из состояния
, состоящее из состояния 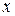 и точки
и точки  из интервала определения системы.
из интервала определения системы.
Сделаем следующие предположения:
1. Будем считать, что функции
 , (В.23)
, (В.23)
а также функции
 (В.24)
(В.24)
непрерывны на  .
.
Отметим, что для ряда задач не требуется существования непрерывных частных производных  и
и 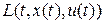 по
по 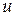 .
.
2. Будем считать, что  , определенная на
, определенная на 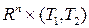 , относится к одному из видов:
, относится к одному из видов:
2.1)  , определенная на
, определенная на 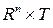 , где
, где 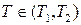 ;
;
2.2)  , определенная на
, определенная на  , где
, где 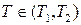 ,
, 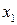 - фиксированный элемент из
- фиксированный элемент из 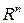 ;
;
2.3)  , определенная на
, определенная на 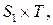 где
где  ̶ гладкое многообразие из
̶ гладкое многообразие из 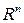 ,
, 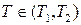 ;
;
2.4)  , где
, где  – непрерывно дифференцируемая функция из
– непрерывно дифференцируемая функция из  в
в 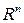 , т.е.
, т.е.  – кривая в
– кривая в 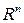 с непрерывно вращающейся касательной;
с непрерывно вращающейся касательной;
2.5) S – гладкое q+1 мерное многообразие функций 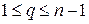 в
в 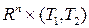 , непрерывно дифференцируемых по t. Иначе говоря, имеется
, непрерывно дифференцируемых по t. Иначе говоря, имеется 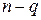 функций
функций  на
на 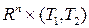 таких, что:
таких, что:
а) 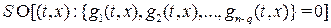 ;
;
б) функции  непрерывны на
непрерывны на 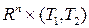 для
для 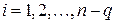 ;
;
в) векторы 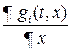
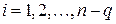 линейно независимы в каждой точке S.
линейно независимы в каждой точке S.
3. Если  (функция конечной стоимости) ̶ заданная действительная функция, определенная на
(функция конечной стоимости) ̶ заданная действительная функция, определенная на 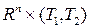 , то будем считать, что:
, то будем считать, что:
3.1) если  имеет вид 2.1 или 2.3, то
имеет вид 2.1 или 2.3, то  и функции
и функции
 непрерывны;
непрерывны;
3.2) если  имеет вид 2.2, то
имеет вид 2.2, то 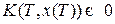 ;
;
3.3) если  имеет вид 2.4, то
имеет вид 2.4, то  и функции
и функции 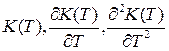 непрерывны;
непрерывны;
3.4) если  имеет вид 2.5, то функции
имеет вид 2.5, то функции
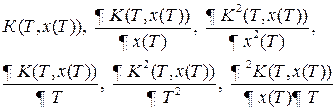
непрерывны.
Образуем функционал, оценивающий эффективность управления:
 . (В.25)
. (В.25)
Этот функционал обычно называют функционалом Больца. Время окончания переходного процесса  может быть задано и не задано. При незаданном верхнем пределе интегрирования функционала (В.25) время окончания переходного процесса
может быть задано и не задано. При незаданном верхнем пределе интегрирования функционала (В.25) время окончания переходного процесса  является дополнительным параметром, который следует определить в дополнение к управляющей функции
является дополнительным параметром, который следует определить в дополнение к управляющей функции  .
.
При 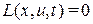 функционал (В.25) принимает вид:
функционал (В.25) принимает вид:
 , (В.26)
, (В.26)
и задачу выбора управляющей функции  , минимизирующей его на объекте (В.22) при предположениях 1,2,3, называют задачей Майера.
, минимизирующей его на объекте (В.22) при предположениях 1,2,3, называют задачей Майера.
Задачу минимизации функционала (В.24) при  и
и  называют обычно задачей Лагранжа.
называют обычно задачей Лагранжа.
Конкретизация выражений (В.22), условий (В.21), предположений 1,2,3 и вида функционала (В.25) порождает различные задачи математического конструирования систем управления.
Определение 14. Задачей оптимального управления по отношению к множеству  , функционалу
, функционалу  , множеству допустимых управлений
, множеству допустимых управлений  и начальному состоянию
и начальному состоянию  в момент
в момент 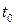 является отыскание
является отыскание  минимизирующего функционал
минимизирующего функционал 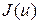 на объекте (В.22).
на объекте (В.22).
Введем понятие «допустимый управляемый процесс ».
Определение 15. Назовем элемент 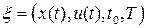 , для которого выполнены все указанные выше условия и ограничения задачи, допустимым управляемым процессом.
, для которого выполнены все указанные выше условия и ограничения задачи, допустимым управляемым процессом.
В зависимости от постановки управления в книге допустимыми элементами 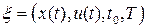 могут быть непрерывно дифференцируемые функции, т.е.
могут быть непрерывно дифференцируемые функции, т.е.  ,
,  или кусочно-гладкие функции
или кусочно-гладкие функции  ,
,  .
.
Задача управления заключается в построении оптимальной стратегии, т.е. в нахождении допустимого управляемого процесса  , минимизирующего функционал вида (В.25) на объекте (В.22).
, минимизирующего функционал вида (В.25) на объекте (В.22).
Типы задач можно условно разделить на три группы. В каждой группе определяющей характеристикой могут быть способы задания функционала качества, ограничений вдоль траектории, краевые условия.
В заключение данного раздела отметим, что существование оптимального управления не является необходимым. Может оказаться, что область допустимых управлений  не содержит управлений, переводящих
не содержит управлений, переводящих  в
в  . Может также оказаться, что
. Может также оказаться, что  содержит несколько оптимальных управлений.
содержит несколько оптимальных управлений.